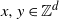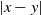Scale-free percolation is a stochastic model for complex networks. In this spatial random graph model, vertices $x,y\in\mathbb{Z}^d$ are linked by an edge with probability depending on independent and identically distributed vertex weights and the Euclidean distance $|x-y|$ . Depending on the various parameters involved, we get a rich phase diagram. We study graph distance and compare it to the Euclidean distance of the vertices. Our main attention is on a regime where graph distances are (poly-)logarithmic in the Euclidean distance. We obtain improved bounds on the logarithmic exponents. In the light tail regime, the correct exponent is identified.