Article contents
Graph distances in scale-free percolation: the logarithmic case
Published online by Cambridge University Press: 11 October 2022
Abstract
Scale-free percolation is a stochastic model for complex networks. In this spatial random graph model, vertices
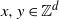 $x,y\in\mathbb{Z}^d$
are linked by an edge with probability depending on independent and identically distributed vertex weights and the Euclidean distance
$x,y\in\mathbb{Z}^d$
are linked by an edge with probability depending on independent and identically distributed vertex weights and the Euclidean distance
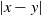 $|x-y|$
. Depending on the various parameters involved, we get a rich phase diagram. We study graph distance and compare it to the Euclidean distance of the vertices. Our main attention is on a regime where graph distances are (poly-)logarithmic in the Euclidean distance. We obtain improved bounds on the logarithmic exponents. In the light tail regime, the correct exponent is identified.
$|x-y|$
. Depending on the various parameters involved, we get a rich phase diagram. We study graph distance and compare it to the Euclidean distance of the vertices. Our main attention is on a regime where graph distances are (poly-)logarithmic in the Euclidean distance. We obtain improved bounds on the logarithmic exponents. In the light tail regime, the correct exponent is identified.
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust
References
- 5
- Cited by



