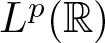1 results
The multilinear spherical maximal function in one dimension
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 25 September 2024, pp. 1045-1059
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
In dimension n = 1, we obtain
$L^{p_1}(\mathbb R) \times\dots\times L^{p_m}(\mathbb R)$ to 
$L^p(\mathbb R)$ boundedness for the multilinear spherical maximal function in the largest possible open set of indices and we provide counterexamples that indicate the optimality of our results.
