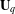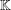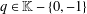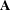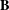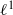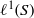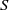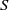2 results
SEMISIMPLICITY OF HECKE AND (WALLED) BRAUER ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 25 October 2016, pp. 1-44
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
ON THE
 $\ast $-SEMISIMPLICITY OF THE
$\ast $-SEMISIMPLICITY OF THE 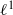 ${\ell }^{1} $-ALGEBRA ON AN ABELIAN
${\ell }^{1} $-ALGEBRA ON AN ABELIAN  $\ast $-SEMIGROUP
$\ast $-SEMIGROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 15 February 2013, pp. 492-498
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation