Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T08:46:23.020Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE $\ast $-SEMISIMPLICITY OF THE 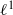${\ell }^{1} $-ALGEBRA ON AN ABELIAN $\ast $-SEMIGROUP

Part of: Topological (rings and) algebras with an involution Commutative Banach algebras and commutative topological algebras Semigroups

Published online by Cambridge University Press:  15 February 2013

S. J. BHATT ,
P. A. DABHI  and
H. V. DEDANIA
S. J. BHATT
Affiliation:
Department of Mathematics, Sardar Patel University, Vallabh Vidyanagar-388120, Gujarat, India email [email protected]@yahoo.com
P. A. DABHI*
Affiliation:
Department of Mathematics, Sardar Patel University, Vallabh Vidyanagar-388120, Gujarat, India email [email protected]@yahoo.com
H. V. DEDANIA
Affiliation:
Department of Mathematics, Sardar Patel University, Vallabh Vidyanagar-388120, Gujarat, India email [email protected]@yahoo.com
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Towards an involutive analogue of a result on the semisimplicity of 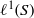${\ell }^{1} (S)$ by Hewitt and Zuckerman, we show that, given an abelian $\ast $-semigroup 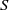$S$, the commutative convolution Banach $\ast $-algebra 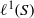${\ell }^{1} (S)$ is $\ast $-semisimple if and only if Hermitian bounded semicharacters on 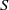$S$ separate the points of 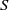$S$; and we search for an intrinsic separation property on 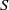$S$ equivalent to $\ast $-semisimplicity. Very many natural involutive analogues of Hewitt and Zuckerman’s separation property are shown not to work, thereby exhibiting intricacies involved in analysis on 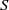$S$.

Keywords

∗-semigroupBanach ∗-algebrasemisimplicity∗-semisimplicity

MSC classification

Secondary: 46K05: General theory of topological algebras with involution 20M14: Commutative semigroups 46J05: General theory of commutative topological algebras
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 88 , Issue 3 , December 2013 , pp. 492 - 498
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Dales, H. G., Banach Algebras and Automatic Continuity, London Mathematical Society Monograph Series, 24 (Clarendon Press, Oxford, 2000).Google Scholar
Dales, H. G., Lau, A. T.-M. and Strauss, D., ‘Banach algebras on semigroups and on their compactifications’, Mem. Amer. Math. Soc. 205 (966) (2010).Google Scholar
Duncan, J. and Paterson, L. T., ‘Amenability for discrete convolution semigroup algebras’, Math. Scand. 66 (1990)141–146.CrossRefGoogle Scholar
Ghlaio, H. M. and Read, C. J., ‘Irregular abelian semigroups with weakly amenable semigroup algebra’, Semigroup Forum 82 (2) (2011), 367–383.Google Scholar
Hewitt, E. and Zuckerman, H. S., ‘The ${l}_{1} $-algebra of a commutative semigroup’, Trans. Amer. Math. Soc. 83 (1956), 70–97.Google Scholar
Sokolsky, A. G., ‘On radicals of semigroup algebras’, Semigroup Forum 59 (1) (1999), 93–105.CrossRefGoogle Scholar