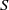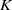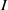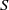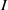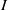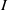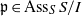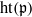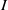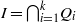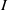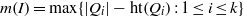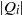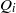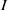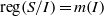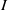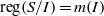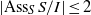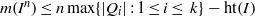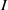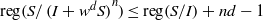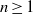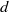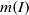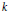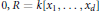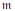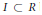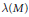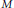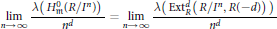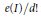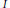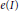Let 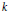$S$ be a polynomial ring over a field $K$ and let $I$ be a monomial ideal of $S$. We say that $I$ is MHC (that is, $I$ satisfies the maximal height condition for the associated primes of $I$) if there exists a prime ideal $\mathfrak{p}\in {\mathrm{Ass} }_{S} \hspace{0.167em} S/ I$ for which $\mathrm{ht} (\mathfrak{p})$ equals the number of indeterminates that appear in the minimal set of monomials generating $I$. Let $I= { \mathop{\bigcap }\nolimits}_{i= 1}^{k} {Q}_{i} $ be the irreducible decomposition of $I$ and let $m(I)= \max \{ \vert Q_{i}\vert - \mathrm{ht} ({Q}_{i} ): 1\leq i\leq k\} $, where $\vert {Q}_{i} \vert $ denotes the total degree of ${Q}_{i} $. Then it can be seen that when $I$ is primary, $\mathrm{reg} (S/ I)= m(I)$. In this paper we improve this result and show that whenever $I$ is MHC, then $\mathrm{reg} (S/ I)= m(I)$ provided $\vert {\mathrm{Ass} }_{S} \hspace{0.167em} S/ I\vert \leq 2$. We also prove that $m({I}^{n} )\leq n\max \{ \vert Q_{i}\vert : 1\leq i\leq ~k\} - \mathrm{ht} (I)$, for all $n\geq 1$. In addition we show that if $I$ is MHC and $w$ is an indeterminate which is not in the monomials generating $I$, then $\mathrm{reg} (S/ \mathop{(I+ {w}^{d} S)}\nolimits ^{n} )\leq \mathrm{reg} (S/ I)+ nd- 1$ for all $n\geq 1$ and $d$ large enough. Finally, we implement an algorithm for the computation of $m(I)$.

Let $k$ be a field of characteristic 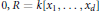$0,\,R\,=\,k\left[ {{x}_{1}},\,\ldots ,\,{{x}_{d}} \right]$ be a polynomial ring, and 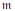$m$ its maximal homogeneous ideal. Let 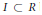$I\,\subset \,R$ be a homogeneous ideal in 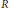$R$. Let 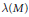$\lambda (M)$ denote the length of an 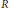$R$-module 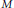$M$. In this paper, we show that

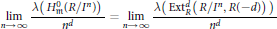$$\underset{x\to \infty }{\mathop{\lim }}\,\,\frac{\lambda \left( H_{m}^{0}\left( R/{{I}^{n}} \right) \right)}{{{n}^{d}}}\,=\,\underset{x\to \infty }{\mathop{\lim }}\,\,\frac{\lambda \left( \text{Ext}_{R}^{d}\left( R/{{I}^{n}},\,R\left( -d \right) \right) \right)}{{{n}^{d}}}$$

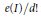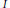always exists. This limit has been shown to be $e(I)/d!$ for $m$-primary ideals $I$ in a local Cohen–Macaulay ring, where 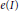$e(I)$ denotes the multiplicity of 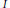$I$. But we find that this limit may not be rational in general. We give an example for which the limit is an irrational number thereby showing that the lengths of these extension modules may not have polynomial growth.

In this paper the asymptotic behavior of the Castelnuovo$ndash;Mumford regularity of powers of a homogeneous ideal I is studied. It is shown that there is a linear bound for the regularity of the powers I whose slope is the maximum degree of a homogeneous generator of I, and that the regularity of I is a linear function for large n. Similar results hold for the integral closures of the powers of I. On the other hand we give examples of ideal for which the regularity of the saturated powers is asymptotically not a linear function, not even a linear function with periodic coefficients.