ON A CLASS OF MONOMIAL IDEALS

Abstract

Let 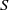$S$ be a polynomial ring over a field 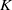$K$ and let 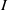$I$ be a monomial ideal of 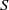$S$. We say that 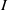$I$ is MHC (that is, 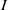$I$ satisfies the maximal height condition for the associated primes of 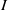$I$) if there exists a prime ideal 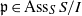$\mathfrak{p}\in {\mathrm{Ass} }_{S} \hspace{0.167em} S/ I$ for which 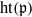$\mathrm{ht} (\mathfrak{p})$ equals the number of indeterminates that appear in the minimal set of monomials generating 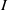$I$. Let 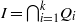$I= { \mathop{\bigcap }\nolimits}_{i= 1}^{k} {Q}_{i} $ be the irreducible decomposition of 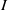$I$ and let 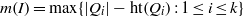$m(I)= \max \{ \vert Q_{i}\vert - \mathrm{ht} ({Q}_{i} ): 1\leq i\leq k\} $, where 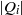$\vert {Q}_{i} \vert $ denotes the total degree of 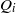${Q}_{i} $. Then it can be seen that when 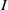$I$ is primary, 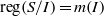$\mathrm{reg} (S/ I)= m(I)$. In this paper we improve this result and show that whenever 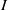$I$ is MHC, then 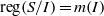$\mathrm{reg} (S/ I)= m(I)$ provided 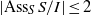$\vert {\mathrm{Ass} }_{S} \hspace{0.167em} S/ I\vert \leq 2$. We also prove that 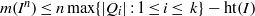$m({I}^{n} )\leq n\max \{ \vert Q_{i}\vert : 1\leq i\leq ~k\} - \mathrm{ht} (I)$, for all 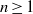$n\geq 1$. In addition we show that if 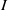$I$ is MHC and 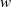$w$ is an indeterminate which is not in the monomials generating 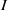$I$, then 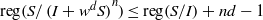$\mathrm{reg} (S/ \mathop{(I+ {w}^{d} S)}\nolimits ^{n} )\leq \mathrm{reg} (S/ I)+ nd- 1$ for all 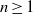$n\geq 1$ and 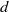$d$ large enough. Finally, we implement an algorithm for the computation of 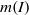$m(I)$.