1 results
Overshoots over curved boundaries. II
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1148-1174
- Print publication:
- December 2004
-
- Article
- Export citation
-
We continue the study of the asymptotic behaviour of a random walk when it exits from a symmetric region of the form {(x, n): |x| ≤ rnb} as r → ∞ which was begun in Part I of this work. In contrast to that paper, we are interested in the case where the probability of exiting at the upper boundary tends to 1. In this scenario we treat the case where the power b lies in the interval [0, 1), and we establish necessary and sufficient conditions for the overshoot to be relatively stable in probability (except for the case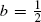
), and for the pth moment of the overshoot to be O(rq) as r → ∞.
), and for the 