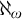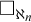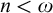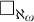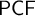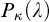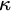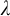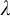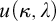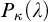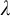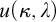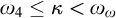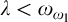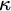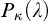5 results
ON COMPACTNESS OF WEAK SQUARE AT SINGULARS OF UNCOUNTABLE COFINALITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 04 January 2024, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE PSEUDOPOWER DICHOTOMY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 10 January 2023, pp. 1655-1681
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
APPLICATIONS OF PCF THEORY TO THE STUDY OF IDEALS ON
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 11 January 2022, pp. 967-994
- Print publication:
- September 2022
-
- Article
- Export citation
PCF structures of height less than ω3
-
- Journal:
- The Journal of Symbolic Logic / Volume 75 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1231-1248
- Print publication:
- December 2010
-
- Article
- Export citation
The PCF conjecture and large cardinals
-
- Journal:
- The Journal of Symbolic Logic / Volume 73 / Issue 2 / June 2008
- Published online by Cambridge University Press:
- 12 March 2014, pp. 674-688
- Print publication:
- June 2008
-
- Article
- Export citation