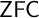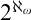We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Club guessing principles were introduced by Shelah as a weakening of Jensen’s diamond. Most spectacularly, they were used to prove Shelah’s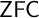 
$\textsf{ZFC}$ bound on 
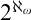$2^{\aleph _\omega }$. These principles have found many other applications: in cardinal arithmetic and PCF theory; in the construction of combinatorial objects on uncountable cardinals such as Jónsson algebras, strong colourings, Souslin trees, and pathological graphs; to the non-existence of universals in model theory; to the non-existence of forcing axioms at higher uncountable cardinals; and many more.
In this paper, the first part of a series, we survey various forms of club guessing that have appeared in the literature, and then systematically study the various ways in which a club guessing sequence can be improved, especially in the way the frequency of guessing is calibrated.
We include an expository section intended for those unfamiliar with club guessing and which can be read independently of the rest of the article.
