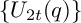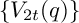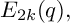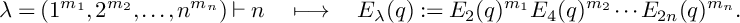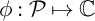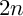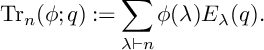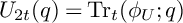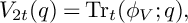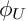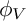We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In his “lost notebook,” Ramanujan used iterated derivatives of two theta functions to define sequences of q-series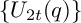 
$\{U_{2t}(q)\}$ and 
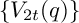$\{V_{2t}(q)\}$ that he claimed to be quasimodular. We give the first explicit proof of this claim by expressing them in terms of “partition Eisenstein series,” extensions of the classical Eisenstein series 
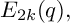$E_{2k}(q),$ defined by 
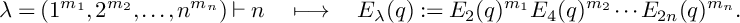$$ \begin{align*}\lambda=(1^{m_1}, 2^{m_2},\dots, n^{m_n}) \vdash n \ \ \ \longmapsto \ \ \ E_{\lambda}(q):= E_2(q)^{m_1} E_4(q)^{m_2}\cdots E_{2n}(q)^{m_n}. \end{align*} $$
For functions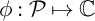 
$\phi : \mathcal {P}\mapsto {\mathbb C}$ on partitions, the weight 
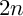$2n$ partition Eisenstein trace is 
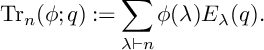$$ \begin{align*}\operatorname{\mathrm{Tr}}_n(\phi;q):=\sum_{\lambda \vdash n} \phi(\lambda)E_{\lambda}(q). \end{align*} $$
For all t, we prove that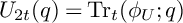 
$U_{2t}(q)=\operatorname {\mathrm {Tr}}_t(\phi _U;q)$ and 
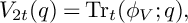$V_{2t}(q)=\operatorname {\mathrm {Tr}}_t(\phi _V;q),$ where 
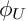$\phi _U$ and 
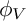$\phi _V$ are natural partition weights, giving the first explicit quasimodular formulas for these series.
