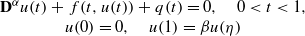2 results
NONTRIVIAL SOLUTIONS FOR STURM–LIOUVILLE SYSTEMS VIA A LOCAL MINIMUM THEOREM FOR FUNCTIONALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 13 June 2013, pp. 8-18
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
-
In this paper, employing a very recent local minimum theorem for differentiable functionals, the existence of at least one nontrivial solution for a class of systems of
$n$ second-order Sturm–Liouville equations is established.
SOLVABILITY FOR A NONLINEAR FRACTIONAL DIFFERENTIAL EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 1 / August 2009
- Published online by Cambridge University Press:
- 19 June 2009, pp. 125-138
- Print publication:
- August 2009
-
- Article
-
- You have access
- Export citation
-
In this paper, we consider the existence of nontrivial solutions for the nonlinear fractional differential equation boundary-value problem (BVP)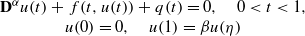
where 1<α≤2, η∈(0,1),β∈ℝ=(−∞,+∞), βηα−1≠1, Dα is the Riemann–Liouville differential operator of order α, and f:[0,1]×ℝ→ℝ is continuous, q(t):[0,1]→[0,+∞) is Lebesgue integrable. We give some sufficient conditions for the existence of nontrivial solutions to the above boundary-value problems. Our approach is based on the Leray–Schauder nonlinear alternative. Particularly, we do not use the nonnegative assumption and monotonicity on f which was essential for the technique used in almost all existed literature.
