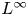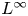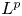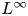2 results
Generalized second order vectorial ∞-eigenvalue problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 March 2024, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On torsional rigidity and principal frequencies: an invitationto the Kohler−Jobin rearrangement technique
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 06 February 2014, pp. 315-338
- Print publication:
- April 2014
-
- Article
- Export citation