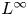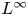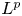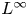1. Introduction and main results
Let $n,\, N \in \mathbb {N}$![]() with $n\geq 2$
with $n\geq 2$![]() , and let $\Omega \Subset \mathbb {R}^n$
, and let $\Omega \Subset \mathbb {R}^n$![]() be a bounded open set with Lipschitz boundary $\partial \Omega$
be a bounded open set with Lipschitz boundary $\partial \Omega$![]() . In this paper we are interested in studying nonlinear second order $L^\infty$
. In this paper we are interested in studying nonlinear second order $L^\infty$![]() eigenvalue problems. Specifically, we investigate the problem of finding a minimizing map $u_{\infty }:\overline {\Omega }\longrightarrow \mathbb {R}^N$
eigenvalue problems. Specifically, we investigate the problem of finding a minimizing map $u_{\infty }:\overline {\Omega }\longrightarrow \mathbb {R}^N$![]() , that solves
, that solves

Additionally, we pursue the necessary conditions that these constrained minimizers must satisfy, in the form of PDEs. In the above, $f: \mathbb {R}^{N \times n^2}_s \longrightarrow \mathbb {R}$![]() and $g :\mathbb {R}^{N} \times \mathbb {R}^{N\times n} \longrightarrow \mathbb {R}$
and $g :\mathbb {R}^{N} \times \mathbb {R}^{N\times n} \longrightarrow \mathbb {R}$![]() are given functions, that will be required to satisfy some natural assumptions, to be discussed later in this section. We note that $\mathbb {R}^{N \times n^2}_s$
are given functions, that will be required to satisfy some natural assumptions, to be discussed later in this section. We note that $\mathbb {R}^{N \times n^2}_s$![]() symbolizes the symmetric subspace of the tensor space $\mathbb {R}^N \otimes (\mathbb {R}^n \otimes \mathbb {R}^n)$
symbolizes the symmetric subspace of the tensor space $\mathbb {R}^N \otimes (\mathbb {R}^n \otimes \mathbb {R}^n)$![]() wherein the hessians of twice differentiable maps $u : \Omega \longrightarrow \mathbb {R}^N$
wherein the hessians of twice differentiable maps $u : \Omega \longrightarrow \mathbb {R}^N$![]() are valued. The functional Sobolev space $W^{2,\infty }_{\mathrm B}(\Omega ;\mathbb {R}^N)$
are valued. The functional Sobolev space $W^{2,\infty }_{\mathrm B}(\Omega ;\mathbb {R}^N)$![]() appearing above will taken to be either of:
appearing above will taken to be either of:

The space $W^{2,\infty }_{\mathrm C}(\Omega ;\mathbb {R}^N)$![]() encompasses the case of so-called clamped boundary conditions, which can be seen as first order Dirichlet or as coupled Dirichlet-Neumann conditions, requiring $|u| =|\mathrm {D} u|= 0$
encompasses the case of so-called clamped boundary conditions, which can be seen as first order Dirichlet or as coupled Dirichlet-Neumann conditions, requiring $|u| =|\mathrm {D} u|= 0$![]() on $\partial \Omega$
on $\partial \Omega$![]() . On the other hand, $W^{2,\infty }_{\mathrm H}(\Omega ;\mathbb {R}^N)$
. On the other hand, $W^{2,\infty }_{\mathrm H}(\Omega ;\mathbb {R}^N)$![]() encompasses the so-called hinged boundary conditions, which are zeroth order Dirichlet conditions, requiring $|u| = 0$
encompasses the so-called hinged boundary conditions, which are zeroth order Dirichlet conditions, requiring $|u| = 0$![]() on $\partial \Omega$
on $\partial \Omega$![]() . This is standard terminology for such problems, see e.g. [Reference Katzourakis and Parini25].
. This is standard terminology for such problems, see e.g. [Reference Katzourakis and Parini25].
Problem (1.1) lies within the Calculus of Variations in $L^{\infty }$![]() , a modern area, initiated by Gunnar Aronsson in the 1960s. Since then this field has undergone a substantial transformation. There are some general complications one must be wary of when tackling $L^{\infty }$
, a modern area, initiated by Gunnar Aronsson in the 1960s. Since then this field has undergone a substantial transformation. There are some general complications one must be wary of when tackling $L^{\infty }$![]() variational problems. For example, the $L^{\infty }$
variational problems. For example, the $L^{\infty }$![]() norm is generally not Gateaux differentiable, therefore the analogue of the Euler–Lagrange equations cannot be derived directly by considering variations. Any supremal functional also has issues with locality in terms of minimization on subdomains. Further, the space itself lacks some fundamental functional analytic properties, such as reflexivity and separability. Higher order problems and problems involving constraints present additional difficulties and have been studied even more sparsely, see e.g. [Reference Aronsson and Barron3, Reference Barron and Jensen4, Reference Clark, Katzourakis and Muha9, Reference Clark and Katzourakis10, Reference Katzourakis20–Reference Katzourakis and Moser24, Reference Katzourakis and Pryer26]. In fact, this paper is an extension of [Reference Katzourakis23] to the second order case, and generalizes part of the results corresponding to the existence of minimizers and the satisfaction of PDEs from [Reference Katzourakis and Parini25]. In turn, the paper [Reference Katzourakis23] generalized results on the scalar case of eigenvalue problems for the $\infty$
norm is generally not Gateaux differentiable, therefore the analogue of the Euler–Lagrange equations cannot be derived directly by considering variations. Any supremal functional also has issues with locality in terms of minimization on subdomains. Further, the space itself lacks some fundamental functional analytic properties, such as reflexivity and separability. Higher order problems and problems involving constraints present additional difficulties and have been studied even more sparsely, see e.g. [Reference Aronsson and Barron3, Reference Barron and Jensen4, Reference Clark, Katzourakis and Muha9, Reference Clark and Katzourakis10, Reference Katzourakis20–Reference Katzourakis and Moser24, Reference Katzourakis and Pryer26]. In fact, this paper is an extension of [Reference Katzourakis23] to the second order case, and generalizes part of the results corresponding to the existence of minimizers and the satisfaction of PDEs from [Reference Katzourakis and Parini25]. In turn, the paper [Reference Katzourakis23] generalized results on the scalar case of eigenvalue problems for the $\infty$![]() -Laplacian ([Reference Juutinen and Lindqvist18, Reference Juutinen, Lindqvist and Manfredi19]). For various interesting results, see for instance [Reference Ansini and Prinari2, Reference Aronsson and Barron3, Reference Bungert and Korolev6, Reference Champion, De Pascale and Prinari8, Reference Kreisbeck and Zappale28–Reference Ribeiro and Zappale31].
-Laplacian ([Reference Juutinen and Lindqvist18, Reference Juutinen, Lindqvist and Manfredi19]). For various interesting results, see for instance [Reference Ansini and Prinari2, Reference Aronsson and Barron3, Reference Bungert and Korolev6, Reference Champion, De Pascale and Prinari8, Reference Kreisbeck and Zappale28–Reference Ribeiro and Zappale31].
The vectorial and higher order nature of the problem we are considering herein precludes the use of standard methods, such as viscosity solutions (see e.g. [1] for a pedagogical introduction). However, we overcome these difficulties by approximating by corresponding $L^p$![]() problems for finite $p$
problems for finite $p$![]() case and let $p\to \infty$
case and let $p\to \infty$![]() . The intuition for using this technique is based on the rudimentary idea that, for a fixed $L^\infty$
. The intuition for using this technique is based on the rudimentary idea that, for a fixed $L^\infty$![]() function on a set of finite measure, its $L^p$
function on a set of finite measure, its $L^p$![]() norm tends to its $L^{\infty }$
norm tends to its $L^{\infty }$![]() norm as $p\to \infty$
norm as $p\to \infty$![]() . This technique is rather standard for $L^\infty$
. This technique is rather standard for $L^\infty$![]() problems, and in the vectorial higher order case we consider herein is essentially the only method known. Even the very recent intrinsic duality method of [Reference Bungert and Korolev6] is limited to scalar-valued first order problems.
problems, and in the vectorial higher order case we consider herein is essentially the only method known. Even the very recent intrinsic duality method of [Reference Bungert and Korolev6] is limited to scalar-valued first order problems.
To state our main result, we now introduce the required hypotheses for the functions $f$![]() and $g$
and $g$![]() :
:


In the above, $\partial f(X)$![]() denotes the the derivative of $f$
denotes the the derivative of $f$![]() whilst $\partial _\eta g$
whilst $\partial _\eta g$![]() and $\partial _P g$
and $\partial _P g$![]() signifies the respective partial derivatives. Additionally ‘:’ and $``\cdot ''$
signifies the respective partial derivatives. Additionally ‘:’ and $``\cdot ''$![]() represent the Euclidean inner products. The terminology of (Morrey) $2$
represent the Euclidean inner products. The terminology of (Morrey) $2$![]() -quasiconvex refers to the standard notion for integral functionals for higher order functionals (see e.g. [Reference Cagnetti7, Reference Dacorogna11, Reference Dal Maso, Fonseca, Leoni and Morini12, Reference Zhou33]), namely
-quasiconvex refers to the standard notion for integral functionals for higher order functionals (see e.g. [Reference Cagnetti7, Reference Dacorogna11, Reference Dal Maso, Fonseca, Leoni and Morini12, Reference Zhou33]), namely
We note that herein we will be using the following function space symbolizations:

Further, we will be using the rescaled $L^p$![]() norms for $p\in [1,\, \infty )$
norms for $p\in [1,\, \infty )$![]() , given by
, given by

Finally, we observe that (1.3)(c), implies that $f>0$![]() on $\mathbb {R}^{N \times n^2}_s\setminus \{0\}$
on $\mathbb {R}^{N \times n^2}_s\setminus \{0\}$![]() , $f(0)=0$
, $f(0)=0$![]() and $f$
and $f$![]() is radially increasing, meaning that $t\mapsto f(tX)$
is radially increasing, meaning that $t\mapsto f(tX)$![]() is increasing on $(0,\, \infty )$
is increasing on $(0,\, \infty )$![]() for any fixed $X\in \mathbb {R}^{N \times n^2}_s\setminus \{0\}$
for any fixed $X\in \mathbb {R}^{N \times n^2}_s\setminus \{0\}$![]() . Similarly, (1.4)(c) implies that $g>0$
. Similarly, (1.4)(c) implies that $g>0$![]() on $(\mathbb {R}^N \times \mathbb {R}^{N\times n}) \setminus \{(0,\,0)\}$
on $(\mathbb {R}^N \times \mathbb {R}^{N\times n}) \setminus \{(0,\,0)\}$![]() , $g(0,\,0)=0$
, $g(0,\,0)=0$![]() and $g$
and $g$![]() is radially increasing on $\mathbb {R}^N \times \mathbb {R}^{N\times n}$
is radially increasing on $\mathbb {R}^N \times \mathbb {R}^{N\times n}$![]() , namely $t\mapsto g(t\eta,\,tP)$
, namely $t\mapsto g(t\eta,\,tP)$![]() is increasing on $(0,\, \infty )$
is increasing on $(0,\, \infty )$![]() for any fixed $(\eta,\,P)\in (\mathbb {R}^N \times \mathbb {R}^{N\times n})\setminus \{(0,\,0)\}$
for any fixed $(\eta,\,P)\in (\mathbb {R}^N \times \mathbb {R}^{N\times n})\setminus \{(0,\,0)\}$![]() .
.
Below is our main result, in which we consider both cases of boundary conditions simultaneously.
Theorem 1.1 Suppose that the assumptions (1.3) and (1.4) hold true. Then:
(A) The problem (1.1) has a solution $u_{\infty }\in W^{2,\infty }_{\mathrm B}(\Omega ;\mathbb {R}^N).$

(B) There exist Radon measures
\[ {\mathrm M}_\infty \in \mathcal{M}\big(\overline{\Omega}; \mathbb{R}_s^{N \times n^2}\big), \quad \nu_{\infty}\in \mathcal{M}(\overline{\Omega}), \]such that (1.5)\begin{align} \int_{\overline{\Omega}} \mathrm{D}^2\phi : \mathrm{d} {\mathrm M}_\infty=\Lambda_{\infty} \int_{\overline{\Omega}} \Big( \partial_\eta g (u_{\infty}, \mathrm{D} u_{\infty})\cdot \phi + \partial_P g (u_{\infty}, \mathrm{D} u_{\infty}) : \mathrm{D} \phi \Big) \, \mathrm{d} \nu_{\infty} \end{align}for all test maps $\phi \in C^2_{\mathrm B}(\overline {\Omega }; \mathbb {R}^N)$
(1.5)\begin{align} \int_{\overline{\Omega}} \mathrm{D}^2\phi : \mathrm{d} {\mathrm M}_\infty=\Lambda_{\infty} \int_{\overline{\Omega}} \Big( \partial_\eta g (u_{\infty}, \mathrm{D} u_{\infty})\cdot \phi + \partial_P g (u_{\infty}, \mathrm{D} u_{\infty}) : \mathrm{D} \phi \Big) \, \mathrm{d} \nu_{\infty} \end{align}for all test maps $\phi \in C^2_{\mathrm B}(\overline {\Omega }; \mathbb {R}^N)$
 , where
(1.6)\begin{equation} \Lambda_{\infty} = \big\|f(\mathrm{D}^2(u_{\infty}) \big\|_{L^{\infty}(\Omega)}>0. \end{equation}Additionally, we have the following a priori lower bound for the eigenvalue
, where
(1.6)\begin{equation} \Lambda_{\infty} = \big\|f(\mathrm{D}^2(u_{\infty}) \big\|_{L^{\infty}(\Omega)}>0. \end{equation}Additionally, we have the following a priori lower bound for the eigenvalue (1.7)\begin{align} \Lambda_{\infty}\geq \Bigg ( \frac{ C_4 } {\mathrm{diam}(\Omega)^\alpha \Big(C(\infty,\Omega) \|\partial_\eta g \|_{L^{\infty}(\{g \leq1\})}+\|\partial_P g \|_{L^{\infty}(\{g \leq1\})}\Big)^\alpha } -C_3 \Bigg)^{\!\!+}, \end{align}where $(\, \cdot \, )^+$
(1.7)\begin{align} \Lambda_{\infty}\geq \Bigg ( \frac{ C_4 } {\mathrm{diam}(\Omega)^\alpha \Big(C(\infty,\Omega) \|\partial_\eta g \|_{L^{\infty}(\{g \leq1\})}+\|\partial_P g \|_{L^{\infty}(\{g \leq1\})}\Big)^\alpha } -C_3 \Bigg)^{\!\!+}, \end{align}where $(\, \cdot \, )^+$
 symbolizes the positive part, and $C(\infty,\,\Omega )$
symbolizes the positive part, and $C(\infty,\,\Omega )$ equals either the constant of the Poincaré inequality (in the case of clamped boundary conditions), or the constant of the Poincaré-Wirtinger inequality (in the case of hinged boundary conditions), both taken for $p=\infty$
equals either the constant of the Poincaré inequality (in the case of clamped boundary conditions), or the constant of the Poincaré-Wirtinger inequality (in the case of hinged boundary conditions), both taken for $p=\infty$ .
.
If additionally the boundary $\partial \Omega$
 is $C^2$
is $C^2$ , we have the a priori upper bound
(1.8)\begin{align} \Lambda_\infty \, & \leq \ C_6 + C_5\frac{2^{5\alpha}}{(c \omega(n))^\alpha} \bigg( \! 1 + \underset{0\leq t \leq 1}{\sup}R(t) \! \bigg)^{\!\!\alpha} \Big(2^{3n} + \underset{i=1,...,n-1}{\max}\big(\|\kappa_i\|_{C^0(\partial\Omega)}\big)^n \Big)^{\!\alpha} \centerdot \nonumber\\ & \quad \centerdot \Bigg\{ 1 + \bigg( \! 1+\frac{C}{\varepsilon_0^{n+1}} \! \bigg) \mathcal{H}^{n-1}(\partial\Omega) + \sum_{i=1}^{n-1} \left\| \frac{ \kappa_i \circ \mathrm{P}_{\Omega} }{ 1 - ( \kappa_i \circ \mathrm{P}_{\Omega})d_\Omega } \right\|_{L^\infty(\{d_\Omega< \varepsilon_0\} \cap \Omega)} \!\!\Bigg\}^{\!\alpha} , \end{align}
, we have the a priori upper bound
(1.8)\begin{align} \Lambda_\infty \, & \leq \ C_6 + C_5\frac{2^{5\alpha}}{(c \omega(n))^\alpha} \bigg( \! 1 + \underset{0\leq t \leq 1}{\sup}R(t) \! \bigg)^{\!\!\alpha} \Big(2^{3n} + \underset{i=1,...,n-1}{\max}\big(\|\kappa_i\|_{C^0(\partial\Omega)}\big)^n \Big)^{\!\alpha} \centerdot \nonumber\\ & \quad \centerdot \Bigg\{ 1 + \bigg( \! 1+\frac{C}{\varepsilon_0^{n+1}} \! \bigg) \mathcal{H}^{n-1}(\partial\Omega) + \sum_{i=1}^{n-1} \left\| \frac{ \kappa_i \circ \mathrm{P}_{\Omega} }{ 1 - ( \kappa_i \circ \mathrm{P}_{\Omega})d_\Omega } \right\|_{L^\infty(\{d_\Omega< \varepsilon_0\} \cap \Omega)} \!\!\Bigg\}^{\!\alpha} , \end{align}
where $c,\,C>0$
 are dimensionless universal constants, $\omega (n)$
are dimensionless universal constants, $\omega (n)$ is the volume of the unit ball in $\mathbb {R}^n$
is the volume of the unit ball in $\mathbb {R}^n$ , $\mathcal {H}^{n-1}(\partial \Omega )$
, $\mathcal {H}^{n-1}(\partial \Omega )$ is the perimeter of $\Omega$
is the perimeter of $\Omega$ , $\{\kappa _1,\,...,\,\kappa _{n-1}\}$
, $\{\kappa _1,\,...,\,\kappa _{n-1}\}$ are the principal curvatures of $\partial \Omega$
are the principal curvatures of $\partial \Omega$ , $\mathrm {P}_{\Omega }$
, $\mathrm {P}_{\Omega }$ is the orthogonal projection on $\partial \Omega$
is the orthogonal projection on $\partial \Omega$ , $d_\Omega$
, $d_\Omega$ the distance function of $\partial \Omega$
the distance function of $\partial \Omega$ , $\varepsilon _0$
, $\varepsilon _0$ is the largest
\[ \varepsilon \in \left(0 , \min\left\{1,\, \underset{i=1,...,n-1}{\min}\frac{1}{ \|\kappa_i\|_{C^0(\partial\Omega)}} \right\}\right), \]for which we have that $d_\Omega \in C^2(\{d_\Omega \leq \varepsilon \} \cap \overline {\Omega })$
is the largest
\[ \varepsilon \in \left(0 , \min\left\{1,\, \underset{i=1,...,n-1}{\min}\frac{1}{ \|\kappa_i\|_{C^0(\partial\Omega)}} \right\}\right), \]for which we have that $d_\Omega \in C^2(\{d_\Omega \leq \varepsilon \} \cap \overline {\Omega })$
 and $R(t)$
and $R(t)$ is the smallest radius of the $N$
is the smallest radius of the $N$ -dimensional ball, for which the sublevel set $\{g\leq t\}$
-dimensional ball, for which the sublevel set $\{g\leq t\}$ is contained into the cylinder $\bar {\mathbb {B}}^N_{R(t)}(0) \times \mathbb {R}^{N\times n}$
is contained into the cylinder $\bar {\mathbb {B}}^N_{R(t)}(0) \times \mathbb {R}^{N\times n}$ , namely
\[ R(t) \,:=\, \inf \Big\{ R>0 \, : \, \{g\leq t\} \subseteq \mathbb{B}^N_R(0) \times \mathbb{R}^{N\times n}\Big\}. \]
, namely
\[ R(t) \,:=\, \inf \Big\{ R>0 \, : \, \{g\leq t\} \subseteq \mathbb{B}^N_R(0) \times \mathbb{R}^{N\times n}\Big\}. \]
(C) The quadruple $(u_{\infty },\, \Lambda _{\infty },\, {\mathrm M}_\infty,\, \nu _{\infty })$
 satisfies the following approximation properties: there exists a sequence of exponents $(p_j)_1^{\infty } \subseteq (n/ \alpha )$
satisfies the following approximation properties: there exists a sequence of exponents $(p_j)_1^{\infty } \subseteq (n/ \alpha )$ where $p_j\to \infty$
where $p_j\to \infty$ as $j\to \infty$
as $j\to \infty$ , and for any $p$
, and for any $p$ , a quadruple
\[ (u_p,\Lambda_p, {\mathrm M}_p, \nu_p)\ \in\ W^{2,\alpha p}_{\mathrm B}(\Omega;\mathbb{R}^N)\times [0, \infty) \times\mathcal{M}\big(\overline{\Omega}; \mathbb{R}_s^{N \times n^2}\big) \times \mathcal{M}(\overline{\Omega}), \]
, a quadruple
\[ (u_p,\Lambda_p, {\mathrm M}_p, \nu_p)\ \in\ W^{2,\alpha p}_{\mathrm B}(\Omega;\mathbb{R}^N)\times [0, \infty) \times\mathcal{M}\big(\overline{\Omega}; \mathbb{R}_s^{N \times n^2}\big) \times \mathcal{M}(\overline{\Omega}), \]
such that

as $p \to \infty$![]() along $(p_j)_1^{\infty }$
along $(p_j)_1^{\infty }$![]() . Further, $u_p$
. Further, $u_p$![]() solves the constrained minimization problem
solves the constrained minimization problem
and $(u_p,\, \Lambda _p)$![]() satisfies
satisfies

for all test maps $\phi \in W^{2,\alpha p}_{\mathrm B}(\Omega ;\mathbb {R}^N)$![]() . Finally, the measures ${\mathrm M}_p,\, \nu _p$
. Finally, the measures ${\mathrm M}_p,\, \nu _p$![]() are given by
are given by

We note that one could pursue optimality in theorem 1.1(A) by using $L^\infty$![]() versions of quasiconvexity, as developed by Barron–Jensen–Wang [Reference Barron, Jensen and Wang5] but adapted to this higher order case, in regards to the existence of $L^\infty$
versions of quasiconvexity, as developed by Barron–Jensen–Wang [Reference Barron, Jensen and Wang5] but adapted to this higher order case, in regards to the existence of $L^\infty$![]() minimizers. However, for parts (B) and (C) of theorem 1.1 regarding the necessary PDE conditions, we do need Morrey $2$
minimizers. However, for parts (B) and (C) of theorem 1.1 regarding the necessary PDE conditions, we do need Morrey $2$![]() -quasiconvexity, as we rely essentially on the existence of solutions to the corresponding Euler–Lagrange equations and the theory of Lagrange multipliers in the finite $p$
-quasiconvexity, as we rely essentially on the existence of solutions to the corresponding Euler–Lagrange equations and the theory of Lagrange multipliers in the finite $p$![]() case. Further, the measures ${\mathrm M}_\infty,\, \nu _{\infty }$
case. Further, the measures ${\mathrm M}_\infty,\, \nu _{\infty }$![]() depend on the minimizer $u_{\infty }$
depend on the minimizer $u_{\infty }$![]() in a non-linear fashion, hence one more could perhaps symbolize them more concisely as ${\mathrm M}_\infty (u_\infty ),\, \nu _{\infty }(u_\infty )$
in a non-linear fashion, hence one more could perhaps symbolize them more concisely as ${\mathrm M}_\infty (u_\infty ),\, \nu _{\infty }(u_\infty )$![]() . Consequently, the significance of these equations is currently understood to be mostly of conceptual value, rather than of computational nature. However, it is possible to obtain further information about the underlying structure of these parametric measure coefficients. This requires techniques such as measure function pairs and mollifications up to the boundary as in [Reference Clark and Katzourakis10, Reference Hutchinson17, Reference Katzourakis23], but to keep the presentation as simple as possible, we refrain from pursuing this -considerably more technical- endeavour, which also requires stronger assumptions.
. Consequently, the significance of these equations is currently understood to be mostly of conceptual value, rather than of computational nature. However, it is possible to obtain further information about the underlying structure of these parametric measure coefficients. This requires techniques such as measure function pairs and mollifications up to the boundary as in [Reference Clark and Katzourakis10, Reference Hutchinson17, Reference Katzourakis23], but to keep the presentation as simple as possible, we refrain from pursuing this -considerably more technical- endeavour, which also requires stronger assumptions.
2. Proofs
In this section we establish theorem 1.1. Its proof is not labelled explicitly, but will be completed by proving a combination of smaller subsidiary results, including a selection of lemmas and propositions.
Before introducing the approximating problem (the $L^p$![]() case for finite $p$
case for finite $p$![]() ), we need to establish a convergence result, which shows that the admissible classes of the $p$
), we need to establish a convergence result, which shows that the admissible classes of the $p$![]() -problems are non-empty. It is required because the function $g$
-problems are non-empty. It is required because the function $g$![]() appearing in the constraint is not assumed to be homogeneous, therefore a standard scaling argument does not suffice.
appearing in the constraint is not assumed to be homogeneous, therefore a standard scaling argument does not suffice.
Lemma 2.1 For any $v\in W^{2,\infty }_{\mathrm B}(\Omega ;\mathbb {R}^N)\setminus \{0\}$![]() , there exists $(t_p)_{p\in (n/\alpha, \infty ]}$
, there exists $(t_p)_{p\in (n/\alpha, \infty ]}$![]() with $t_p\to t_{\infty }$
with $t_p\to t_{\infty }$![]() as $p\to \infty$
as $p\to \infty$![]() , such that
, such that
for all $p\in (n/\alpha,\, \infty ]$![]() . Further, if $\|g(v,\, \mathrm {D} v) \|_{L^{\infty }(\Omega )}=1$
. Further, if $\|g(v,\, \mathrm {D} v) \|_{L^{\infty }(\Omega )}=1$![]() , then $t_{\infty }=1$
, then $t_{\infty }=1$![]() .
.
Proof Proof of lemma 2.1
Fix $v\in W^{2,\infty }_{\mathrm B}(\Omega ;\mathbb {R}^N)\setminus \{0\}$![]() and define
and define
It follows that $\rho _{\infty }(0)=0$![]() and $\rho _{\infty }$
and $\rho _{\infty }$![]() is continuous on $[0,\, \infty )$
is continuous on $[0,\, \infty )$![]() . We will now show that $\rho _{\infty }$
. We will now show that $\rho _{\infty }$![]() is strictly increasing. We first show it is non-decreasing. For any $s>0$
is strictly increasing. We first show it is non-decreasing. For any $s>0$![]() and $(\eta,\,P) \in \mathbb {R}^N \times \mathbb {R}^{N\times n} \setminus \{(0,\,0)\}$
and $(\eta,\,P) \in \mathbb {R}^N \times \mathbb {R}^{N\times n} \setminus \{(0,\,0)\}$![]() , our assumption (1.4)(c) implies
, our assumption (1.4)(c) implies

thus $s\mapsto g(s\eta,\, sP)$![]() is increasing on $(0,\, \infty )$
is increasing on $(0,\, \infty )$![]() . Hence, for any $x\in \overline {\Omega }$
. Hence, for any $x\in \overline {\Omega }$![]() and $t>s\geq 0$
and $t>s\geq 0$![]() we have $g(tv(x),\, t \mathrm {D} v(x)) \geq g(sv(x),\, s\mathrm {D} v(x))$
we have $g(tv(x),\, t \mathrm {D} v(x)) \geq g(sv(x),\, s\mathrm {D} v(x))$![]() , which yields,
, which yields,
We proceed to demonstrate that $t\mapsto \rho _{\infty }(t)$![]() is actually strictly monotonic over $(0,\,\infty )$
is actually strictly monotonic over $(0,\,\infty )$![]() . Fix $t_0>0$
. Fix $t_0>0$![]() . By Danskin's theorem [Reference Danskin13], the derivative from the right $\rho '(t_0^+)$
. By Danskin's theorem [Reference Danskin13], the derivative from the right $\rho '(t_0^+)$![]() exists, and is given by the formula
exists, and is given by the formula
where
Hence, by (1.4)(c) we estimate

This implies that $\rho _{\infty }$![]() is strictly increasing on $(0,\,\infty )$
is strictly increasing on $(0,\,\infty )$![]() . Next, recall that $g$
. Next, recall that $g$![]() is coercive by assumption (1.4)(b), namely $g(s\eta,\, sP)\to \infty$
is coercive by assumption (1.4)(b), namely $g(s\eta,\, sP)\to \infty$![]() as $s\to \infty$
as $s\to \infty$![]() , for fixed $(\eta,\,P)\neq (0,\,0)$
, for fixed $(\eta,\,P)\neq (0,\,0)$![]() . Thus, for any fixed point $\overline {x}\in \Omega$
. Thus, for any fixed point $\overline {x}\in \Omega$![]() with $(v(\overline {x}),\,\mathrm {D} v(\overline {x}))\ne (0,\,0)$
with $(v(\overline {x}),\,\mathrm {D} v(\overline {x}))\ne (0,\,0)$![]() , which exists because by assumption $v\not \equiv 0$
, which exists because by assumption $v\not \equiv 0$![]() , we have
, we have
Since $\rho _\infty (0)=0$![]() and $\rho _{\infty }(t) \to \infty$
and $\rho _{\infty }(t) \to \infty$![]() as $t\to \infty$
as $t\to \infty$![]() , by continuity and the intermediate value theorem, there exists a number $t_\infty >0$
, by continuity and the intermediate value theorem, there exists a number $t_\infty >0$![]() such that $\rho _{\infty }(t_{\infty })=1$
such that $\rho _{\infty }(t_{\infty })=1$![]() , that is
, that is
If $\|g(v,\, \mathrm {D} v)\|_{L^{\infty }(\Omega )}=1$![]() , then $t_{\infty }=1$
, then $t_{\infty }=1$![]() , as a result of the strict monotonicity of $\rho _{\infty }$
, as a result of the strict monotonicity of $\rho _{\infty }$![]() . Now let us fix $p\in (n/\alpha,\, \infty )$
. Now let us fix $p\in (n/\alpha,\, \infty )$![]() and define the continuous function
and define the continuous function
Since $g(0,\,0)=0$![]() , it follows that $\rho _p(0)=0$
, it follows that $\rho _p(0)=0$![]() and that
and that
By Morrey's theorem and our assumptions, we have that $v\in C^1(\overline {\Omega };\mathbb {R}^N)\setminus \{0\}$![]() , therefore $\mathcal {L}^n( \{(v,\,\mathrm {D} v)\ne (0,\,0)\} )>0$
, therefore $\mathcal {L}^n( \{(v,\,\mathrm {D} v)\ne (0,\,0)\} )>0$![]() . Consider the family of functions $\{g(tv,\, t\mathrm {D} v)^p \}_{t>0}$
. Consider the family of functions $\{g(tv,\, t\mathrm {D} v)^p \}_{t>0}$![]() , defined on $\{(v,\,\mathrm {D} v)\ne (0,\,0)\}\subseteq \Omega$
, defined on $\{(v,\,\mathrm {D} v)\ne (0,\,0)\}\subseteq \Omega$![]() . By the monotonicity of $s\mapsto g(s\eta,\, sP)$
. By the monotonicity of $s\mapsto g(s\eta,\, sP)$![]() on $(0,\,\infty )$
on $(0,\,\infty )$![]() for $(\eta,\,P)\neq (0,\,0)$
for $(\eta,\,P)\neq (0,\,0)$![]() , for $s< t$
, for $s< t$![]() we have
we have
Since $g(tv,\, t\mathrm {D} v)^p \to \infty$![]() pointwise on $\{(v,\,\mathrm {D} v)\ne (0,\,0)\}$
pointwise on $\{(v,\,\mathrm {D} v)\ne (0,\,0)\}$![]() as $t \to \infty$
as $t \to \infty$![]() , by the monotone convergence theorem, we infer that
, by the monotone convergence theorem, we infer that
as $t\to \infty$![]() . As a consequence, $\rho _p(t)\to \infty$
. As a consequence, $\rho _p(t)\to \infty$![]() as $t\to \infty$
as $t\to \infty$![]() . Since $\rho _p(0)=0$
. Since $\rho _p(0)=0$![]() , by the intermediate value theorem there exists $t_p>0$
, by the intermediate value theorem there exists $t_p>0$![]() such that $\rho _p(t_p)=1$
such that $\rho _p(t_p)=1$![]() , namely
, namely
For the sake of contradiction, suppose that $t_p \not \to t_{\infty }$![]() , as $p\to \infty$
, as $p\to \infty$![]() . In this case, there exists a subsequence $(t_{p_j})_1^{\infty }\subseteq (n/\alpha,\, \infty )$
. In this case, there exists a subsequence $(t_{p_j})_1^{\infty }\subseteq (n/\alpha,\, \infty )$![]() and $t_0\in [0,\, t_{\infty }) \cup (t_{\infty },\, \infty ]$
and $t_0\in [0,\, t_{\infty }) \cup (t_{\infty },\, \infty ]$![]() such that $t_{p_j}\to t_0$
such that $t_{p_j}\to t_0$![]() as $j\to \infty$
as $j\to \infty$![]() . Further, $(t_{p_j})_1^{\infty }$
. Further, $(t_{p_j})_1^{\infty }$![]() can assumed to be either monotonically increasing or decreasing. We first prove that $t_0$
can assumed to be either monotonically increasing or decreasing. We first prove that $t_0$![]() is finite. If $t_0=\infty$
is finite. If $t_0=\infty$![]() , then the sequence $(t_{p_j})_1^{\infty }$
, then the sequence $(t_{p_j})_1^{\infty }$![]() can be selected to be monotonically increasing. Therefore, by arguing as before, $g(t_{p_j}v,\, t_{p_j} \mathrm {D} v)\nearrow \infty$
can be selected to be monotonically increasing. Therefore, by arguing as before, $g(t_{p_j}v,\, t_{p_j} \mathrm {D} v)\nearrow \infty$![]() as $j\to \infty$
as $j\to \infty$![]() , pointwise on $\{(v,\,\mathrm {D} v)\ne (0,\,0)\}$
, pointwise on $\{(v,\,\mathrm {D} v)\ne (0,\,0)\}$![]() , and the monotone convergence theorem provides the contradiction
, and the monotone convergence theorem provides the contradiction
Consequently, we have that $t_0\in [0,\, t_{\infty }) \cup (t_{\infty },\, \infty )$![]() . Since $(t_{p_j}v,\, t_{p_j}\mathrm {D} v)\to (t_0 v,\, t_0 \mathrm {D} v)$
. Since $(t_{p_j}v,\, t_{p_j}\mathrm {D} v)\to (t_0 v,\, t_0 \mathrm {D} v)$![]() uniformly on $\overline {\Omega }$
uniformly on $\overline {\Omega }$![]() as $j\to \infty$
as $j\to \infty$![]() , we calculate
, we calculate

By passing to the limit as $j\to \infty$![]() , we obtain a contradiction if $t_\infty \ne t_0$
, we obtain a contradiction if $t_\infty \ne t_0$![]() , because $\rho _{\infty }$
, because $\rho _{\infty }$![]() is a strictly increasing function and $\rho _{\infty }(t_\infty )=1$
is a strictly increasing function and $\rho _{\infty }(t_\infty )=1$![]() . In conclusion, $t_p\to t_{\infty }$
. In conclusion, $t_p\to t_{\infty }$![]() as $p\to \infty$
as $p\to \infty$![]() .
.
Utilizing the above result we can now show existence for the approximating minimization problem for $p<\infty$![]() .
.
Lemma 2.2 For any $p>n/ \alpha$![]() , the minimization problem (1.10) has a solution $u_p \in W^{2,\alpha p}_{\mathrm B}(\Omega ;\mathbb {R}^N)$
, the minimization problem (1.10) has a solution $u_p \in W^{2,\alpha p}_{\mathrm B}(\Omega ;\mathbb {R}^N)$![]() .
.
Proof Proof of lemma 2.2
Let us fix $p\in (n/ \alpha,\, \infty )$![]() and $v_0 \in W^{2,\infty }_{\mathrm B}(\Omega ;\mathbb {R}^N)$
and $v_0 \in W^{2,\infty }_{\mathrm B}(\Omega ;\mathbb {R}^N)$![]() where $v_0\, \not \equiv \, 0$
where $v_0\, \not \equiv \, 0$![]() . By application of lemma 2.1, there exists $t_p>0$
. By application of lemma 2.1, there exists $t_p>0$![]() such that $\|g(t_p v_0,\, t_p\mathrm {D} v_0)\|_{L^p(\Omega )}=1$
such that $\|g(t_p v_0,\, t_p\mathrm {D} v_0)\|_{L^p(\Omega )}=1$![]() implying that $t_p v_0$
implying that $t_p v_0$![]() is indeed an element of the admissible class of (1.10). Hence, we deduce that the admissible class is non empty. Further, by assumption (1.3)(b), $f$
is indeed an element of the admissible class of (1.10). Hence, we deduce that the admissible class is non empty. Further, by assumption (1.3)(b), $f$![]() is (Morrey) $2$
is (Morrey) $2$![]() -quasiconvex. We now confirm that $f^p$
-quasiconvex. We now confirm that $f^p$![]() is also (Morrey) $2$
is also (Morrey) $2$![]() -quasiconvex function, as a consequence of Jensen's inequality: for any fixed $X\in \smash {\mathbb {R}^{N \times n^2}_s}$
-quasiconvex function, as a consequence of Jensen's inequality: for any fixed $X\in \smash {\mathbb {R}^{N \times n^2}_s}$![]() and any $\phi \in W^{2,\infty }_0(\Omega ;\mathbb {R}^N)$
and any $\phi \in W^{2,\infty }_0(\Omega ;\mathbb {R}^N)$![]() , we have
, we have
By assumption by assumption (1.3)(d), we have for some new $C_5(p),\,C_6(p)>0$![]() that
that
for any $X\in \smash {\mathbb {R}^{N \times n^2}_s}$![]() . Moreover, by [Reference Zhou33, Theorem 3.6] we have that the functional $v \mapsto \|f(\mathrm {D}^2v)\|_{L^{p}(\Omega )}$
. Moreover, by [Reference Zhou33, Theorem 3.6] we have that the functional $v \mapsto \|f(\mathrm {D}^2v)\|_{L^{p}(\Omega )}$![]() is weakly lower semi-continuous on $W^{2,\alpha p}(\Omega ;\mathbb {R}^N)$
is weakly lower semi-continuous on $W^{2,\alpha p}(\Omega ;\mathbb {R}^N)$![]() and therefore the same is true over the closed subspace $W^{2,\alpha p}_{\mathrm B}(\Omega ;\mathbb {R}^N)$
and therefore the same is true over the closed subspace $W^{2,\alpha p}_{\mathrm B}(\Omega ;\mathbb {R}^N)$![]() . Let $(u_i)_{1}^{\infty }$
. Let $(u_i)_{1}^{\infty }$![]() be a minimizing sequence for (1.10). As $f\geq 0$
be a minimizing sequence for (1.10). As $f\geq 0$![]() , it is clear that $\inf _{i\in \mathbb {N}} \|f(\mathrm {D}^2u_i)\|_{L^{p}(\Omega )}\geq 0$
, it is clear that $\inf _{i\in \mathbb {N}} \|f(\mathrm {D}^2u_i)\|_{L^{p}(\Omega )}\geq 0$![]() . Since the admissible class is non-empty, the infimum is finite. Additionally, by (1.3)(d), we have the bound
. Since the admissible class is non-empty, the infimum is finite. Additionally, by (1.3)(d), we have the bound

Now we show that the functional is coercive in $W^{2,\alpha p}_{\mathrm B}(\Omega ;\mathbb {R}^N)$![]() , arguing separately for either case of boundary conditions. By assumption (1.3)(d) and the Poincaré inequality, for any $u\in W^{2,\alpha p}_{\mathrm C}(\Omega ;\mathbb {R}^N)$
, arguing separately for either case of boundary conditions. By assumption (1.3)(d) and the Poincaré inequality, for any $u\in W^{2,\alpha p}_{\mathrm C}(\Omega ;\mathbb {R}^N)$![]() (satisfying $|u|=|\mathrm {D} u|=0$
(satisfying $|u|=|\mathrm {D} u|=0$![]() on $\partial \Omega$
on $\partial \Omega$![]() ), we have
), we have

for a new constant $C_4'=C_4(p)>0$![]() . Hence, for any $u\in W^{2,\alpha p}_{\mathrm C}(\Omega ;\mathbb {R}^N)$
. Hence, for any $u\in W^{2,\alpha p}_{\mathrm C}(\Omega ;\mathbb {R}^N)$![]() ,
,
The above estimate is also true when $u\in W^{2,\alpha p}_{\mathrm H}(\Omega ;\mathbb {R}^N)$![]() , but since in this case we have only $|u|=0$
, but since in this case we have only $|u|=0$![]() on $\partial \Omega$
on $\partial \Omega$![]() , it requires an additional justification. By the Poincaré-Wirtinger inequality involving averages, for any $u\in W^{2,\alpha p}_{\mathrm H}(\Omega ;\mathbb {R}^N)$
, it requires an additional justification. By the Poincaré-Wirtinger inequality involving averages, for any $u\in W^{2,\alpha p}_{\mathrm H}(\Omega ;\mathbb {R}^N)$![]() we have
we have

where $C=C(\alpha,\,p,\,\Omega )>0$![]() is a constant. Since $|u|=0$
is a constant. Since $|u|=0$![]() on $\partial \Omega$
on $\partial \Omega$![]() , by the Gauss-Green theorem we have
, by the Gauss-Green theorem we have
where $\mathcal {H}^{n-1}$![]() denotes the $(n-1)$
denotes the $(n-1)$![]() -dimensional Hausdorff measure. In conclusion,
-dimensional Hausdorff measure. In conclusion,
for any $u\in W^{2,\alpha p}_{\mathrm H}(\Omega ;\mathbb {R}^N)$![]() . The above estimate together with the standard Poincaré inequality applied to $u$
. The above estimate together with the standard Poincaré inequality applied to $u$![]() itself allow to infer that (2.1) holds for any $u\in W^{2,\alpha p}_{\mathrm B}(\Omega ;\mathbb {R}^N)$
itself allow to infer that (2.1) holds for any $u\in W^{2,\alpha p}_{\mathrm B}(\Omega ;\mathbb {R}^N)$![]() in both cases of boundary conditions. Returning to our minimizing sequence, by standard compactness results, exists $u_p \in W^{2,\alpha p}_{\mathrm H}(\Omega ;\mathbb {R}^N)$
in both cases of boundary conditions. Returning to our minimizing sequence, by standard compactness results, exists $u_p \in W^{2,\alpha p}_{\mathrm H}(\Omega ;\mathbb {R}^N)$![]() such that $u_i \, -\!\!\!\!\!-\!\!\!\!\rightharpoonup u _p$
such that $u_i \, -\!\!\!\!\!-\!\!\!\!\rightharpoonup u _p$![]() in $W^{2,\alpha p}_{\mathrm B}(\Omega ;\mathbb {R}^N)$
in $W^{2,\alpha p}_{\mathrm B}(\Omega ;\mathbb {R}^N)$![]() , as $i\to \infty$
, as $i\to \infty$![]() along a subsequence of indices. Additionally, by the Morrey estimate we have that $u_i\longrightarrow u_p$
along a subsequence of indices. Additionally, by the Morrey estimate we have that $u_i\longrightarrow u_p$![]() in $C^1(\overline {\Omega }; \mathbb {R}^N)$
in $C^1(\overline {\Omega }; \mathbb {R}^N)$![]() as $i\to \infty$
as $i\to \infty$![]() , along perhaps a further subsequence. Since $u\mapsto \|g(u,\, \mathrm {D} u)\|_{L^p(\Omega )}$
, along perhaps a further subsequence. Since $u\mapsto \|g(u,\, \mathrm {D} u)\|_{L^p(\Omega )}$![]() is weakly continuous on $W^{2,\alpha p}_{\mathrm B}(\Omega ;\mathbb {R}^N)$
is weakly continuous on $W^{2,\alpha p}_{\mathrm B}(\Omega ;\mathbb {R}^N)$![]() , the admissible class is weakly closed in $W^{2,\alpha p}(\Omega ;\mathbb {R}^N)$
, the admissible class is weakly closed in $W^{2,\alpha p}(\Omega ;\mathbb {R}^N)$![]() and hence we may pass to the limit in the constraint. By weak lower semicontinuity of the functional, it follows that a minimizer $u_p$
and hence we may pass to the limit in the constraint. By weak lower semicontinuity of the functional, it follows that a minimizer $u_p$![]() which satisfies (1.10) does indeed exist.
which satisfies (1.10) does indeed exist.
Now we describe the necessary conditions (Euler–Lagrange equations) that approximating minimizer $u_p$![]() must satisfy. These equations will involve a Lagrange multiplier, emerging from the constraint $\|g(\cdot,\, \mathrm {D} (\cdot ))\|_{L^p(\Omega )}=1$
must satisfy. These equations will involve a Lagrange multiplier, emerging from the constraint $\|g(\cdot,\, \mathrm {D} (\cdot ))\|_{L^p(\Omega )}=1$![]() .
.
Lemma 2.3 For any $p>n/ \alpha$![]() , let $u_p$
, let $u_p$![]() be the minimizer of (1.10) procured by lemma 2.2. Then, there exists $\lambda _p \in \mathbb {R}$
be the minimizer of (1.10) procured by lemma 2.2. Then, there exists $\lambda _p \in \mathbb {R}$![]() such that the pair $(u_p,\, \lambda _p)$
such that the pair $(u_p,\, \lambda _p)$![]() satisfies the following PDE system
satisfies the following PDE system

for all test maps $\phi \in W^{2,\alpha p}_{\mathrm B}(\Omega ;\mathbb {R}^N).$![]()
In particular, it follows that in both cases $u_p$![]() is a weak solution in $W^{2,\alpha p}(\Omega ;\mathbb {R}^N)$
is a weak solution in $W^{2,\alpha p}(\Omega ;\mathbb {R}^N)$![]() to
to

where we have used the notation $\mathrm {D}^2 : F = \sum _{i,j=1}^n \mathrm {D}^2_{ij} F_{ij}$![]() , when $F \in C^2(\Omega ;\mathbb {R}^{n \times n})$
, when $F \in C^2(\Omega ;\mathbb {R}^{n \times n})$![]() , which is equivalent to the double divergence (applied once column-wise and once row-wise). Note that in the case of hinged boundary data, we have an additional natural boundary condition arising (since $\mathrm {D} u$
, which is equivalent to the double divergence (applied once column-wise and once row-wise). Note that in the case of hinged boundary data, we have an additional natural boundary condition arising (since $\mathrm {D} u$![]() is free on $\partial \Omega$
is free on $\partial \Omega$![]() ), we we will not make an particular use of this extra information in the sequel, therefore we refrain from discussing it explicitly.
), we we will not make an particular use of this extra information in the sequel, therefore we refrain from discussing it explicitly.
Proof Proof of lemma 2.3
The result follows by standard results on Lagrange multipliers in Banach spaces (see e.g. [Reference Zeidler32, p. 278]), by utilizing assumption (1.3)(d), which guarantees that the functional is Gateaux differentiable.
Now we establish some further results regarding the family of eigenvalues.
Lemma 2.4 Consider the family of pairs of eigenvectors-eigenvalues $\{(u_p,\,\lambda _p)\}_{p > n/ \alpha }$![]() , given by lemma 2.3. Then, for any $p>n/\alpha$
, given by lemma 2.3. Then, for any $p>n/\alpha$![]() , there exists $\Lambda _p>0$
, there exists $\Lambda _p>0$![]() such that
such that
Further, by setting
we have the bounds

Proof Proof of lemma 2.4
We begin by showing that $L_p>0$![]() , namely the infimum over the admissible class of the $p$
, namely the infimum over the admissible class of the $p$![]() -approximating minimization problem is strictly positive, owing to the constraint and our assumptions (1.3)-(1.4). Indeed, there is only one map $u\in W^{2,\alpha p}_{\mathrm B}(\Omega ;\mathbb {R}^N)$
-approximating minimization problem is strictly positive, owing to the constraint and our assumptions (1.3)-(1.4). Indeed, there is only one map $u\in W^{2,\alpha p}_{\mathrm B}(\Omega ;\mathbb {R}^N)$![]() for which $\|f(\mathrm {D}^2u)\|_{L^p(\Omega )}=0$
for which $\|f(\mathrm {D}^2u)\|_{L^p(\Omega )}=0$![]() , namely $u_0\equiv 0$
, namely $u_0\equiv 0$![]() , but this is not an element of the admissible class since $\|g(u_0,\, \mathrm {D} u_0)\|_{L^p(\Omega )}=0$
, but this is not an element of the admissible class since $\|g(u_0,\, \mathrm {D} u_0)\|_{L^p(\Omega )}=0$![]() . Now consider the Euler–Lagrange equations in lemma 2.3 and select $\phi :=u_p$
. Now consider the Euler–Lagrange equations in lemma 2.3 and select $\phi :=u_p$![]() , to obtain
, to obtain

As $f,\,g\geq 0$![]() we can manipulate the respective assumptions (1.3)(c) and (1.4)(c) to produce the following bounds:
we can manipulate the respective assumptions (1.3)(c) and (1.4)(c) to produce the following bounds:

The above two estimates, combined with the Euler–Lagrange equations, imply that $\lambda _p>0$![]() . Hence, we may therefore define $\Lambda _p:=(\lambda _p)^{\frac {1}{p}}>0$
. Hence, we may therefore define $\Lambda _p:=(\lambda _p)^{\frac {1}{p}}>0$![]() . We will now obtain the upper and lower bounds. We determine the lower bound as follows:
. We will now obtain the upper and lower bounds. We determine the lower bound as follows:

Hence,

The upper bound is determined analogously, by reversing the direction of the inequalities. Combining both bounds, we obtain the desired estimate.
Proposition 2.5 There exists $(u_{\infty },\, \Lambda _{\infty })\in W^{2,\infty }_{\mathrm B}(\Omega ;\mathbb {R}^N)\times (0,\, \infty )$![]() such that, along a sequence $(p_j)_1^{\infty }$
such that, along a sequence $(p_j)_1^{\infty }$![]() of exponents, we have
of exponents, we have

as $p_j\to \infty$![]() . Additionally, $u_{\infty }$
. Additionally, $u_{\infty }$![]() solves the minimization problem (1.1) and $\Lambda _{\infty }$
solves the minimization problem (1.1) and $\Lambda _{\infty }$![]() is given by (1.6). Finally $\Lambda _{\infty }$
is given by (1.6). Finally $\Lambda _{\infty }$![]() satisfies the uniform bounds (1.7).
satisfies the uniform bounds (1.7).
Proof Proof of proposition 2.5
Fix $p>n/\alpha,\, q\leq p$![]() and a map $v_0\in W^{2,\infty }_{\mathrm B}(\Omega ;\mathbb {R}^N)\setminus \{0\}$
and a map $v_0\in W^{2,\infty }_{\mathrm B}(\Omega ;\mathbb {R}^N)\setminus \{0\}$![]() . Then, by lemma 2.1 there exists $(t_p)_{p\in (n/\alpha, \infty ]} \subseteq (0,\, \infty )$
. Then, by lemma 2.1 there exists $(t_p)_{p\in (n/\alpha, \infty ]} \subseteq (0,\, \infty )$![]() such that $t_p \to t_{\infty }$
such that $t_p \to t_{\infty }$![]() as $p\to \infty$
as $p\to \infty$![]() and satisfying $\|g(t_p v_0,\, t_p \mathrm {D} v_0)\|_{L^p(\Omega )}=1$
and satisfying $\|g(t_p v_0,\, t_p \mathrm {D} v_0)\|_{L^p(\Omega )}=1$![]() for all $p\in (n/\alpha,\, \infty ]$
for all $p\in (n/\alpha,\, \infty ]$![]() . By Hölder's inequality and minimality, we have the following estimate
. By Hölder's inequality and minimality, we have the following estimate

for some $K>0$![]() . By (1.3)(d), we have the bound $f^q(X)\geq C_4(q)|X|^{\alpha q}- C_3(q)$
. By (1.3)(d), we have the bound $f^q(X)\geq C_4(q)|X|^{\alpha q}- C_3(q)$![]() for some constants $C_3(q),\, C_4(q)>0$
for some constants $C_3(q),\, C_4(q)>0$![]() and all $X\in \mathbb {R}^{N \times n^2}_s.$
and all $X\in \mathbb {R}^{N \times n^2}_s.$![]() By the previous bound, we conclude that
By the previous bound, we conclude that
for some $q$![]() -dependent constant. By arguing as in the proof of lemma 2.2 through the use of Poincaré inequalities, we can conclude in both cases of boundary conditions with the bound
-dependent constant. By arguing as in the proof of lemma 2.2 through the use of Poincaré inequalities, we can conclude in both cases of boundary conditions with the bound
for a new $q$![]() -dependent constant $C'(q)>0$
-dependent constant $C'(q)>0$![]() . Standard compactness in Sobolev spaces and a diagonal sequence argument imply the existence of a mapping
. Standard compactness in Sobolev spaces and a diagonal sequence argument imply the existence of a mapping
and a subsequence $(p_j)_1^\infty$![]() such that the desired modes of convergence hold true as $p_j\to \infty$
such that the desired modes of convergence hold true as $p_j\to \infty$![]() along this subsequence of indices. Fix a map $v\in W^{2, \infty }_{\mathrm B}(\Omega ; \mathbb {R}^N)$
along this subsequence of indices. Fix a map $v\in W^{2, \infty }_{\mathrm B}(\Omega ; \mathbb {R}^N)$![]() satisfying the required constraint, namely $\|g(v,\, \mathrm {D} v) \|_{L^{\infty }(\Omega )}=1$
satisfying the required constraint, namely $\|g(v,\, \mathrm {D} v) \|_{L^{\infty }(\Omega )}=1$![]() . In view of lemma 2.1, there exists $(t_p)_{p\in (n/\alpha, \infty )}\subseteq (0,\, \infty )$
. In view of lemma 2.1, there exists $(t_p)_{p\in (n/\alpha, \infty )}\subseteq (0,\, \infty )$![]() satisfying that $t_p\to 1$
satisfying that $t_p\to 1$![]() as $p\to \infty$
as $p\to \infty$![]() , and additionally $\|g(t_p v,\, t_p \mathrm {D} v)\|_{L^p(\Omega )}=1$
, and additionally $\|g(t_p v,\, t_p \mathrm {D} v)\|_{L^p(\Omega )}=1$![]() for all $p>n/\alpha$
for all $p>n/\alpha$![]() . By Hölder's inequality, the definition of $L_p$
. By Hölder's inequality, the definition of $L_p$![]() and minimality, we have
and minimality, we have
for any such $v$![]() . By the weak lower semi-continuity of the functional on $W^{2, \alpha q}_{\mathrm B}(\Omega ; \mathbb {R}^N)$
. By the weak lower semi-continuity of the functional on $W^{2, \alpha q}_{\mathrm B}(\Omega ; \mathbb {R}^N)$![]() , we may let $p_j \to \infty$
, we may let $p_j \to \infty$![]() to obtain
to obtain

Now we may let $q\to \infty$![]() in the above bound, hence producing
in the above bound, hence producing
for all mappings $v\in W^{2, \infty }_{\mathrm B}(\Omega ; \mathbb {R}^N)$![]() satisfying the constraint $\|g(v,\, \mathrm {D} v)\|_{L^{\infty }(\Omega )}=1$
satisfying the constraint $\|g(v,\, \mathrm {D} v)\|_{L^{\infty }(\Omega )}=1$![]() . If we additionally show that in fact $u_{\infty }$
. If we additionally show that in fact $u_{\infty }$![]() satisfies the constraint in (1.1), then the above estimate shows both that it is the desired minimizers (by choosing $v:=u_\infty$
satisfies the constraint in (1.1), then the above estimate shows both that it is the desired minimizers (by choosing $v:=u_\infty$![]() ), and also that the sequence $(L_{p_j})_1^\infty$
), and also that the sequence $(L_{p_j})_1^\infty$![]() converges to the infimum. Now we show that this is indeed the case. In view of assumption (1.3)(d), the previous estimate implies also that $\mathrm {D}^2u_{\infty }\in \smash {L^{\infty }(\Omega ; \mathbb {R}_s^{N \times n^2})}$
converges to the infimum. Now we show that this is indeed the case. In view of assumption (1.3)(d), the previous estimate implies also that $\mathrm {D}^2u_{\infty }\in \smash {L^{\infty }(\Omega ; \mathbb {R}_s^{N \times n^2})}$![]() , which together with Poincaré inequalities (as in the proof of lemma 2.2) shows that in fact $u_{\infty } \in W^{2, \infty }_{\mathrm B}(\Omega ; \mathbb {R}^N)$
, which together with Poincaré inequalities (as in the proof of lemma 2.2) shows that in fact $u_{\infty } \in W^{2, \infty }_{\mathrm B}(\Omega ; \mathbb {R}^N)$![]() . By the continuity of the function $g$
. By the continuity of the function $g$![]() and the fact that $u_{p} \longrightarrow u_\infty$
and the fact that $u_{p} \longrightarrow u_\infty$![]() in $C^1 (\overline {\Omega };\mathbb {R}^N )$
in $C^1 (\overline {\Omega };\mathbb {R}^N )$![]() , we have
, we have

as $p_j\to \infty$![]() . Consequently, $u_{\infty }$
. Consequently, $u_{\infty }$![]() satisfies the constraint, and therefore lies in the admissible class of (1.1). Since $v$
satisfies the constraint, and therefore lies in the admissible class of (1.1). Since $v$![]() was arbitrary in the energy bound, we conclude that $u_{\infty }$
was arbitrary in the energy bound, we conclude that $u_{\infty }$![]() in fact solves (1.1). let us now define
in fact solves (1.1). let us now define
We now show that $\Lambda _{\infty }>0$![]() . Indeed, by our assumptions (1.3)–(1.4), there is only one map in $W^{2,\infty }(\Omega ;\mathbb {R}^N)$
. Indeed, by our assumptions (1.3)–(1.4), there is only one map in $W^{2,\infty }(\Omega ;\mathbb {R}^N)$![]() satisfying $\|f(\mathrm {D}^2u_0)\|_{L^{\infty }(\Omega )}=0$
satisfying $\|f(\mathrm {D}^2u_0)\|_{L^{\infty }(\Omega )}=0$![]() and $|u_0|\equiv 0$
and $|u_0|\equiv 0$![]() on $\partial \Omega$
on $\partial \Omega$![]() , namely the trivial map $u_0\equiv 0$
, namely the trivial map $u_0\equiv 0$![]() , but $u_0$
, but $u_0$![]() is not contained in the admissible class of (1.1) because $\|g(u_0,\, \mathrm {D} u_0)\|_{L^{\infty }(\Omega )}=0$
is not contained in the admissible class of (1.1) because $\|g(u_0,\, \mathrm {D} u_0)\|_{L^{\infty }(\Omega )}=0$![]() . We now show that $\Lambda _p \longrightarrow \Lambda _{\infty }$
. We now show that $\Lambda _p \longrightarrow \Lambda _{\infty }$![]() as $p_j \to \infty$
as $p_j \to \infty$![]() . By our earlier energy estimate, we have $L_p\longrightarrow \Lambda _{\infty }$
. By our earlier energy estimate, we have $L_p\longrightarrow \Lambda _{\infty }$![]() as $p_j \to \infty$
as $p_j \to \infty$![]() . By lemma 2.4, we have
. By lemma 2.4, we have

and therefore $\Lambda _p \longrightarrow \Lambda _{\infty }$![]() as $p_j \to \infty$
as $p_j \to \infty$![]() . To complete the proof we must deduce the claimed bounds for $\Lambda _{\infty }$
. To complete the proof we must deduce the claimed bounds for $\Lambda _{\infty }$![]() . We first establish the lower bound. By utilizing the Poincaré and Poincaré-Wirtinger inequalities (recall the proof of lemma 2.2) and that $g(0,\,0)=0$
. We first establish the lower bound. By utilizing the Poincaré and Poincaré-Wirtinger inequalities (recall the proof of lemma 2.2) and that $g(0,\,0)=0$![]() , we estimate
, we estimate

where $C(\infty,\,\Omega )>0$![]() is the maximum of the Poincaré and the Poincaré-Wirtinger inequality constants on $\Omega$
is the maximum of the Poincaré and the Poincaré-Wirtinger inequality constants on $\Omega$![]() for $p=\infty$
for $p=\infty$![]() (with the former being equal to $\mathrm {diam}(\Omega )$
(with the former being equal to $\mathrm {diam}(\Omega )$![]() ). As $g\geq 0$
). As $g\geq 0$![]() and $\|g(u_{\infty },\, \mathrm {D} u_{\infty })\|_{L^{\infty }(\Omega )}=1$
and $\|g(u_{\infty },\, \mathrm {D} u_{\infty })\|_{L^{\infty }(\Omega )}=1$![]() , we conclude that $0\leq g(u_{\infty },\, \mathrm {D} u_{\infty })\leq 1$
, we conclude that $0\leq g(u_{\infty },\, \mathrm {D} u_{\infty })\leq 1$![]() on $\overline {\Omega }$
on $\overline {\Omega }$![]() . Hence $(u_{\infty },\, \mathrm {D} u_{\infty })(\overline {\Omega }) \subseteq \{0\leq g \leq 1\}=\{g \leq 1\}$
. Hence $(u_{\infty },\, \mathrm {D} u_{\infty })(\overline {\Omega }) \subseteq \{0\leq g \leq 1\}=\{g \leq 1\}$![]() . Thus
. Thus
Rearranging assumption (1.3)(d), we may write $|X|\leq C_4^{-\frac {1}{\alpha }}(f(X)+C_3)^{\frac {1}{\alpha }}$![]() , for any $X \in \mathbb {R}^{N \times n^2}_s$
, for any $X \in \mathbb {R}^{N \times n^2}_s$![]() . Combining this inequality with the previous bound, we deduce
. Combining this inequality with the previous bound, we deduce

which leads directly to the claimed lower bound for the eigenvalue.
Now we establish the upper bound for $\Lambda _\infty$![]() . Since $\Omega$
. Since $\Omega$![]() is by assumption a bounded domain with $C^2$
is by assumption a bounded domain with $C^2$![]() boundary, by standard results (see e.g. [Reference Gilbarg and Trudinger16, Sec. 14.6]), the distance function
boundary, by standard results (see e.g. [Reference Gilbarg and Trudinger16, Sec. 14.6]), the distance function
which is in $W^{1,\infty }_{\mathrm {loc}}(\mathbb {R}^n)$![]() , is also $C^2$
, is also $C^2$![]() on an inner tubular neighbourhood of $\partial \Omega$
on an inner tubular neighbourhood of $\partial \Omega$![]() , namely there exists $\varepsilon _0 \in (0,\,1)$
, namely there exists $\varepsilon _0 \in (0,\,1)$![]() such that
such that
Let us also for convenience symbolize $\Omega _\varepsilon := \{d_\Omega >\varepsilon \} \cap \hspace {1pt} \Omega$![]() . Let us also fix $k\in \{1,\,2\}$
. Let us also fix $k\in \{1,\,2\}$![]() , a unit vector $e\in \mathbb {R}^N$
, a unit vector $e\in \mathbb {R}^N$![]() and $\zeta \in C^2(\mathbb {R}^n)$
and $\zeta \in C^2(\mathbb {R}^n)$![]() with $\zeta \equiv 0$
with $\zeta \equiv 0$![]() on $\Omega _{\varepsilon _0}$
on $\Omega _{\varepsilon _0}$![]() . Then, for any $t_0>0$
. Then, for any $t_0>0$![]() , the map $\xi _0 := t_0 (d_\Omega )^k\zeta e$
, the map $\xi _0 := t_0 (d_\Omega )^k\zeta e$![]() satisfies
satisfies
Since $\mathrm {d}_\Omega =0$![]() on $\partial \Omega$
on $\partial \Omega$![]() and also $\mathrm {D}(\mathrm {d}^2_\Omega )=0$
and also $\mathrm {D}(\mathrm {d}^2_\Omega )=0$![]() on $\partial \Omega$
on $\partial \Omega$![]() , it follows that $\xi _0 \in W^{2,\infty }_{\mathrm H}(\Omega ;\mathbb {R}^N)$
, it follows that $\xi _0 \in W^{2,\infty }_{\mathrm H}(\Omega ;\mathbb {R}^N)$![]() if $k=1$
if $k=1$![]() , whilst $\xi _0 \in W^{2,\infty }_{\mathrm C}(\Omega ;\mathbb {R}^N)$
, whilst $\xi _0 \in W^{2,\infty }_{\mathrm C}(\Omega ;\mathbb {R}^N)$![]() if $k=2$
if $k=2$![]() . We will consider both cases simultaneously and declare this as
. We will consider both cases simultaneously and declare this as
By lemma 2.1, we can adjust the constant $t_0>0$![]() to arrange
to arrange
Hence, $\xi _0$![]() is in the admissible class of the minimization problem (1.1). By minimality and assumption (1.3), we have the estimate
is in the admissible class of the minimization problem (1.1). By minimality and assumption (1.3), we have the estimate
By a direct computation, we have
on $\overline {\Omega }$![]() . For any $x\in \overline {\Omega ^{\varepsilon _0}}$
. For any $x\in \overline {\Omega ^{\varepsilon _0}}$![]() , let us set $\mathrm {P}_{\Omega }(x) := \mathrm {Proj}_{\partial \Omega }(x)$
, let us set $\mathrm {P}_{\Omega }(x) := \mathrm {Proj}_{\partial \Omega }(x)$![]() . Then, by [Reference Gilbarg and Trudinger16, Sec. 14.6, L. 14.17], it follows that $|x- \mathrm {P}_{\Omega }(x)|=d_\Omega (x)$
. Then, by [Reference Gilbarg and Trudinger16, Sec. 14.6, L. 14.17], it follows that $|x- \mathrm {P}_{\Omega }(x)|=d_\Omega (x)$![]() , and we also have the next estimates
, and we also have the next estimates

where $\{\kappa _1,\,...,\,\kappa _{n-1}\}$![]() are the principal curvatures of $\partial \Omega$
are the principal curvatures of $\partial \Omega$![]() . By (2.3)-(2.5) we have the estimate
. By (2.3)-(2.5) we have the estimate

It remains to select an appropriate function $\zeta$![]() in order to estimate its derivatives in terms of the geometry of $\Omega$
in order to estimate its derivatives in terms of the geometry of $\Omega$![]() , and to obtain an estimate for $t_0$
, and to obtain an estimate for $t_0$![]() . For the former, we argue as follows. Let $(\eta ^\delta )_{\delta >0}$
. For the former, we argue as follows. Let $(\eta ^\delta )_{\delta >0}$![]() be the family of standard mollifying kernels, as e.g. in [Reference Katzourakis and Varvaruca27]. We select
be the family of standard mollifying kernels, as e.g. in [Reference Katzourakis and Varvaruca27]. We select
which is the regularization of the characteristic of the complement of $\Omega$![]() . It follows that this function satisfies the initial requirements, and additionally
. It follows that this function satisfies the initial requirements, and additionally

by standard properties of convolutions and the differentiation of BV functions (see e.g. [Reference Folland15] and [Reference Evans and Gariepy14, Ch. 5, p. 198]). Then, by Young's inequality for convolutions, we have the estimates

for some universal constant $C>0$![]() . Now we work towards an estimate for $t_0$
. Now we work towards an estimate for $t_0$![]() appearing in (2.3). By assumption (1.4), we have that the sublevel sets $\{g\leq t\}$
appearing in (2.3). By assumption (1.4), we have that the sublevel sets $\{g\leq t\}$![]() are compact in $\mathbb {R}^N \times \mathbb {R}^{N\times n}$
are compact in $\mathbb {R}^N \times \mathbb {R}^{N\times n}$![]() for any $t\geq 0$
for any $t\geq 0$![]() . Let us define $R(t)$
. Let us define $R(t)$![]() as the smallest radius of the $N$
as the smallest radius of the $N$![]() -dimensional ball, for which $\{g\leq t\}$
-dimensional ball, for which $\{g\leq t\}$![]() is contained into the cylinder $\bar{\mathbb {B}}^N_{R(t)}(0) \times \mathbb {R}^{N\times n}$
is contained into the cylinder $\bar{\mathbb {B}}^N_{R(t)}(0) \times \mathbb {R}^{N\times n}$![]() :
:
Then, we define a strictly increasing function $\rho : [0,\,\infty ) \longrightarrow [0,\,\infty )$![]() by setting
by setting
Then, $\rho$![]() satisfies $\rho (0)=0$
satisfies $\rho (0)=0$![]() , and also that
, and also that
for any $t\geq 0$![]() . Further, by construction,
. Further, by construction,
The above imply
Next, since $d_\Omega ^k\zeta$![]() vanishes on $\partial \Omega \cup \overline {\Omega _{\varepsilon _0}}$
vanishes on $\partial \Omega \cup \overline {\Omega _{\varepsilon _0}}$![]() and $g(0,\,0)=0$
and $g(0,\,0)=0$![]() , we have
, we have

Since $d_\Omega \equiv \varepsilon _0/4$![]() on $\partial \Omega ^{\varepsilon _0/4}$
on $\partial \Omega ^{\varepsilon _0/4}$![]() , and $\rho ^{-1}$
, and $\rho ^{-1}$![]() is strictly increasing, the above implies
is strictly increasing, the above implies

Now we estimate $\max _{\partial \Omega ^{\varepsilon _0/4}}\zeta$![]() from below. Fix $x\in \partial \Omega ^{\varepsilon _0/4}$
from below. Fix $x\in \partial \Omega ^{\varepsilon _0/4}$![]() . Then, since the standard mollifying kernel $\eta$
. Then, since the standard mollifying kernel $\eta$![]() is a radial function (see e.g. [Reference Katzourakis and Varvaruca27]), there exists a universal $c>0$
is a radial function (see e.g. [Reference Katzourakis and Varvaruca27]), there exists a universal $c>0$![]() such that $\eta \geq c$
such that $\eta \geq c$![]() on $\mathbb {B}_{1/2}(0)$
on $\mathbb {B}_{1/2}(0)$![]() . Therefore,
. Therefore,

for any $x\in \partial \Omega ^{\varepsilon _0/4}$![]() . Finally, since $\partial \Omega$
. Finally, since $\partial \Omega$![]() satisfies the exterior sphere condition, the set $\mathbb {B}_{\varepsilon _0/2}(x) \setminus \Omega$
satisfies the exterior sphere condition, the set $\mathbb {B}_{\varepsilon _0/2}(x) \setminus \Omega$![]() contains a ball $\mathbb {B}_r(\bar x)$
contains a ball $\mathbb {B}_r(\bar x)$![]() centred at some point $\bar x$
centred at some point $\bar x$![]() , where the maximum possible radius $\bar r$
, where the maximum possible radius $\bar r$![]() is given by
is given by
Therefore, if $\omega (n)$![]() is the volume of the unit ball in $\mathbb {R}^n$
is the volume of the unit ball in $\mathbb {R}^n$![]() ,
,

for any $x\in \partial \Omega ^{\varepsilon _0/4}$![]() . Hence, we have established the lower bound
. Hence, we have established the lower bound
By (2.10) and (2.11), we infer (since $\varepsilon _0<1$![]() and $k\in \{1,\,2\}$
and $k\in \{1,\,2\}$![]() ) that
) that

By (2.6), (2.7), and (2.12), we conclude with the following upper bound for the eigenvalue:

The claimed estimate (1.8) follows from (2.13) above, by recalling that in view of (2.8)–(2.9), we have
and also that the last term of (2.13) is finite at least when

The result ensues.
Lemma 2.6 For any $p>(n/\alpha ) +2$![]() , there exist measures $\nu _{\infty }\in \mathcal {M}(\overline {\Omega })$
, there exist measures $\nu _{\infty }\in \mathcal {M}(\overline {\Omega })$![]() and ${\mathrm M}_\infty \in \mathcal {M}(\overline {\Omega }; \mathbb {R}^{N \times n^2}_s)$
and ${\mathrm M}_\infty \in \mathcal {M}(\overline {\Omega }; \mathbb {R}^{N \times n^2}_s)$![]() such that, along perhaps a further sequence $(p_j)_1^{\infty }$
such that, along perhaps a further sequence $(p_j)_1^{\infty }$![]() of exponents, we have
of exponents, we have
as $j\to \infty$![]() , where the approximating measures $\nu _p,\,\mathrm M_p$
, where the approximating measures $\nu _p,\,\mathrm M_p$![]() are given by (1.12).
are given by (1.12).
Proof Proof of lemma 2.6
We begin by noting that since $g\,{\geq}\, 0$![]() and ${\|g(u_p,\, \mathrm {D} u_p)\|_{L^p(\Omega )}\,{=}\,1}$
and ${\|g(u_p,\, \mathrm {D} u_p)\|_{L^p(\Omega )}\,{=}\,1}$![]() , in view of (1.12) we have the bound
, in view of (1.12) we have the bound

By the sequential weak$^*$![]() compactness of the space of Radon measures we can conclude that $\nu _{p} \overset{\, *_{\phantom{|}}}{{\smash{\, -\!\!\!\!-\!\!\!\!\rightharpoonup}}\, } \nu _\infty,\, \text {in } \mathcal {M}(\overline {\Omega })$
compactness of the space of Radon measures we can conclude that $\nu _{p} \overset{\, *_{\phantom{|}}}{{\smash{\, -\!\!\!\!-\!\!\!\!\rightharpoonup}}\, } \nu _\infty,\, \text {in } \mathcal {M}(\overline {\Omega })$![]() up to the passage to a further subsequence. Now we establish appropriate total variation bounds for the measure $\mathrm M_p$
up to the passage to a further subsequence. Now we establish appropriate total variation bounds for the measure $\mathrm M_p$![]() . Since $f\geq 0$
. Since $f\geq 0$![]() , by the bounds of lemma 2.4 and assumption (1.3), we estimate (for sufficiently large $p$
, by the bounds of lemma 2.4 and assumption (1.3), we estimate (for sufficiently large $p$![]() )
)

Hence,

The above bound allows to conclude that $\mathrm M_{p} \overset{\, *_{\phantom{|}}}{{\smash{\, -\!\!\!\!-\!\!\!\!\rightharpoonup}}\, } {\mathrm M}_\infty \text {in} \ \mathcal {M}(\overline {\Omega }; \mathbb {R}^{N \times n^2}_s)$![]() , along perhaps a further subsequence of indices $(p_j)_1^\infty$
, along perhaps a further subsequence of indices $(p_j)_1^\infty$![]() as $j\to \infty$
as $j\to \infty$![]() .
.
To conclude the proof of theorem 1.1 we must ensure the PDE system (1.5) is indeed satisfied by the quadruple $(u_{\infty },\, \Lambda _{\infty },\, {\mathrm M}_\infty,\, \nu _{\infty })$![]() .
.
Lemma 2.7 If ${\mathrm M}_\infty \in \mathcal {M}(\overline {\Omega }; \mathbb {R}^{N \times n^2}_s)$![]() and $\nu _{\infty }\in \mathcal {M}(\overline {\Omega })$
and $\nu _{\infty }\in \mathcal {M}(\overline {\Omega })$![]() are the measures obtained in lemma 2.6, then the pair $(u_{\infty },\, \Lambda _{\infty })$
are the measures obtained in lemma 2.6, then the pair $(u_{\infty },\, \Lambda _{\infty })$![]() satisfies (1.5) for all $\phi \in C^2_{\mathrm B}(\overline {\Omega };\mathbb {R}^N)$
satisfies (1.5) for all $\phi \in C^2_{\mathrm B}(\overline {\Omega };\mathbb {R}^N)$![]() .
.
Proof Proof of lemma 2.7
Fix a test function $\phi \in C^2_{\mathrm B}(\overline {\Omega };\mathbb {R}^N)$![]() and $p>n/\alpha +2$
and $p>n/\alpha +2$![]() by (1.12) we may rewrite the PDE system in (1.11) as follows
by (1.12) we may rewrite the PDE system in (1.11) as follows
Recall that, by proposition 2.5, we have $\Lambda _p\longrightarrow \Lambda _{\infty }$![]() and also $(u_p,\,\mathrm {D} u_p)\longrightarrow (u_{\infty },\,\mathrm {D} u_{\infty })$
and also $(u_p,\,\mathrm {D} u_p)\longrightarrow (u_{\infty },\,\mathrm {D} u_{\infty })$![]() uniformly on $\overline {\Omega }$
uniformly on $\overline {\Omega }$![]() , as $p_j\to \infty$
, as $p_j\to \infty$![]() . By assumption (1.4)(a), we have that $\partial _\eta g (u_p,\,\mathrm {D} u_p)\longrightarrow \partial _\eta g (u_{\infty },\, \mathrm {D} u_{\infty })$
. By assumption (1.4)(a), we have that $\partial _\eta g (u_p,\,\mathrm {D} u_p)\longrightarrow \partial _\eta g (u_{\infty },\, \mathrm {D} u_{\infty })$![]() and also $\partial _P g (u_p,\,\mathrm {D} u_p)\longrightarrow \partial _P g (u_{\infty },\, \mathrm {D} u_{\infty })$
and also $\partial _P g (u_p,\,\mathrm {D} u_p)\longrightarrow \partial _P g (u_{\infty },\, \mathrm {D} u_{\infty })$![]() , both uniformly on $\overline {\Omega }$
, both uniformly on $\overline {\Omega }$![]() , as $p_j\to \infty$
, as $p_j\to \infty$![]() . The result ensues by invoking lemma 2.6, in conjunction with weak$^*$
. The result ensues by invoking lemma 2.6, in conjunction with weak$^*$![]() -strong continuity of the duality pairing $\mathcal {M}(\overline {\Omega })\times C(\overline {\Omega }) \longrightarrow \mathbb {R}$
-strong continuity of the duality pairing $\mathcal {M}(\overline {\Omega })\times C(\overline {\Omega }) \longrightarrow \mathbb {R}$![]() .
.
Acknowledgements
The authors would like to thank the referee of this paper for their careful reading of the manuscript, as well as their constructive suggestions.
E.C. has been financially supported through the UK EPSRC scholarship GS19-055