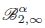In this article, our aim is to estimate the successive derivatives of the stationarydensity f of a strictly stationary and β-mixing process (Xt)t≥0. This process is observed at discrete timest = 0,Δ,...,nΔ. Thesampling interval Δ can be fixed or small. We use a penalizedleast-square approach to compute adaptive estimators. If the derivativef(j) belongs to the Besov space \hbox{$\rond{B}_{2,\infty}^{\alpha}$}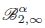$B_{\mathrm{2}\mathit{,}\mathrm{\infty }}^{\mathit{\alpha }}$, then our estimator converges at rate (nΔ)−α/(2α+2j+1). Then we consider a diffusion with known diffusioncoefficient. We use the particular form of the stationary density to compute an adaptiveestimator of its first derivative f′. When the sampling intervalΔ tends to 0, and when the diffusion coefficient is known, theconvergence rate of our estimator is (nΔ)−α/(2α+1). When the diffusion coefficient is known, we alsoconstruct a quotient estimator of the drift for low-frequency data.

In this paper, we study the problem of non parametric estimationof the stationary marginal density f of an α or aβ-mixing process, observed either in continuous time or indiscrete time. We present an unified framework allowing to dealwith many different cases. We consider a collection of finitedimensional linear regular spaces. We estimate f using aprojection estimator built on a data driven selected linear spaceamong the collection. This data driven choice is performed via theminimization of a penalized contrast. We state non asymptotic riskbounds, regarding to the integrated quadratic risk, for ourestimators, in both cases of mixing. We show that they areadaptive in the minimax sense over a large class of Besov balls.In discrete time, we also provide a result for model selectionamong an exponentially large collection of models (non regularcase).

We present a scenario for the evolution of massive stars in which a new mixing mechanism (named global diffusion) is taken into account. This type of mixing stands on the critical Reynolds number and radiative viscosity (Schatzman 1977) and allows mixing of material to take place between the core and the surface during the whole evolution on a very slow time scale. The physical processes triggering global diffusion deserve further study. We find that stellar models of massive stars calculated with global diffusion offer interesting clues to understanding the properties of Wolf-Rayet stars and their location in the HRD.

In this paper we prove that the limiting distribution of the general bulk queue exists and is independent of the initial conditions if and only if the traffic intensity is less than one. We further generalize the following heavy traffic results of the GI/G/1 model to the general bulk queue model. When ρ > 1 or ρ = 1 the waiting time is distributed approximately as a Gaussian variable and the absolute value of a Gaussian variable, respectively. The exponential approximation is derived from the Wiener–Hopf matrix equations established in a previous paper while the unstable case ρ ≧ 1 is treated by means of functional central limit theorems for mixing processes.