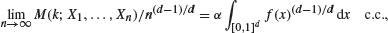Consider the basic location problem in which k locations from among n given points X1,…,Xn are to be chosen so as to minimize the sum M(k; X1,…,Xn) of the distances of each point to the nearest location. It is assumed that no location can serve more than a fixed finite number D of points. When the Xi, i ≥ 1, are i.i.d. random variables with values in [0,1]d and when k = ⌈n/(D+1)⌉ we show that
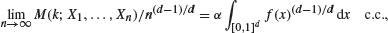
where α := α(D,d) is a positive constant, f is the density of the absolutely continuous part of the law of X1, and c.c. denotes complete convergence.