A generalized correlated random walk is a process of partial sums 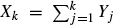 such that (X, Y) forms a Markov chain. For a sequence (Xn) of such processes in which each
such that (X, Y) forms a Markov chain. For a sequence (Xn) of such processes in which each 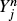 takes only two values, we prove weak convergence to a diffusion process whose generator is explicitly described in terms of the limiting behaviour of the transition probabilities for the Yn. Applications include asymptotics of option replication under transaction costs and approximation of a given diffusion by regular recombining binomial trees.
takes only two values, we prove weak convergence to a diffusion process whose generator is explicitly described in terms of the limiting behaviour of the transition probabilities for the Yn. Applications include asymptotics of option replication under transaction costs and approximation of a given diffusion by regular recombining binomial trees.

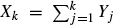 such that (
such that (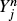 takes only two values, we prove weak convergence to a diffusion process whose generator is explicitly described in terms of the limiting behaviour of the transition probabilities for the
takes only two values, we prove weak convergence to a diffusion process whose generator is explicitly described in terms of the limiting behaviour of the transition probabilities for the 