Various weighted 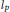 ${{l}_{p}}$-norm inequalities in convolutions are derived by a simple and general principle whose
${{l}_{p}}$-norm inequalities in convolutions are derived by a simple and general principle whose 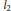 ${{l}_{2}}$ version was obtained by using the theory of reproducing kernels. Applications to the Riemann zeta function and a difference equation are also considered.
${{l}_{2}}$ version was obtained by using the theory of reproducing kernels. Applications to the Riemann zeta function and a difference equation are also considered.