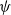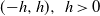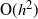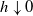We study the quasi-stationary behavior of the birth–death process with an entrance boundary at infinity. We give by the h-transform an alternative and simpler proof for the exponential convergence of conditioned distributions to a unique quasi-stationary distribution in the total variation norm. In addition, we also show that starting from any initial distribution the conditional probability converges to the unique quasi-stationary distribution exponentially fast in the $\psi$ -norm.

For a Brownian bridge from 0 to y, we prove that the mean of the first exit time from the interval $\left( -h,h \right),h>0$ , behaves as ${\mathrm{O}}(h^2)$ when $h \downarrow 0$ . Similar behaviour is also seen to hold for the three-dimensional Bessel bridge. For the Brownian bridge and three-dimensional Bessel bridge, this mean of the first exit time has a puzzling representation in terms of the Kolmogorov distribution. The result regarding the Brownian bridge is applied to provide a detailed proof of an estimate needed by Walsh to determine the convergence of the binomial tree scheme for European options.

This paper examines a problem of importance to the telecommunications industry. In the design of modern ATM switches, it is necessary to use simulation to estimate the probability that a queue within the switch exceeds a given large value. Since these are extremely small probabilities, importance sampling methods must be used. Here we obtain a change of measure for a broad class of models with direct applicability to ATM switches.

We consider a model with A independent sources of cells where each source is modeled by a Markov renewal point process with batch arrivals. We do not assume the sources are necessarily identically distributed, nor that batch sizes are independent of the state of the Markov process. These arrivals join a queue served by multiple independent servers, each with service times also modeled as a Markov renewal process. We only discuss a time-slotted system. The queue is viewed as the additive component of a Markov additive chain subject to the constraint that the additive component remains non-negative. We apply the theory in McDonald (1999) to obtain the asymptotics of the tail of the distribution of the queue size in steady state plus the asymptotics of the mean time between large deviations of the queue size.