Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-29T01:15:40.806Z Has data issue: false hasContentIssue false
  • English
  • Français

On first exit times and their means for Brownian bridges

Part of: Markov processes Mathematical finance

Published online by Cambridge University Press:  01 October 2019

Christel Geiss ,
Antti Luoto  and
Paavo Salminen
Christel Geiss*
Affiliation:
University of Jyväskylä
Antti Luoto*
Affiliation:
University of Jyväskylä
Paavo Salminen*
Affiliation:
Åbo Akademi University
*
* Postal address: Department of Mathematics and Statistics, University of Jyväskylä, PO Box 35 (MaD), FI-40014, Finland.
* Postal address: Department of Mathematics and Statistics, University of Jyväskylä, PO Box 35 (MaD), FI-40014, Finland.
**** Postal address: Faculty of Science and Engineering, Åbo Akademi University, Domkyrkotorget 3, 20500 Åbo, Finland. Email address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a Brownian bridge from 0 to y, we prove that the mean of the first exit time from the interval 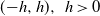$\left( -h,h \right),h>0$ , behaves as 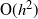${\mathrm{O}}(h^2)$ when 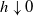$h \downarrow 0$ . Similar behaviour is also seen to hold for the three-dimensional Bessel bridge. For the Brownian bridge and three-dimensional Bessel bridge, this mean of the first exit time has a puzzling representation in terms of the Kolmogorov distribution. The result regarding the Brownian bridge is applied to provide a detailed proof of an estimate needed by Walsh to determine the convergence of the binomial tree scheme for European options.

Keywords

Bessel processBlack–Scholes modelBrownian motiondiffusion processh-transformlast exit timePoisson summation formula

MSC classification

Primary: 60J65: Brownian motion 60J60: Diffusion processes
Secondary: 91G60: Numerical methods (including Monte Carlo methods)
Type
Research Papers
Information
Journal of Applied Probability , Volume 56 , Issue 3 , September 2019 , pp. 701 - 722
Copyright
© Applied Probability Trust 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Biane, P., Pitman, J. and Yor, M. (2001). Probability laws related to the Jacobi theta and Riemann zeta functions, and Brownian excursions. Bull. Amer. Math. Soc. (N.S.) 38, 435–465.CrossRefGoogle Scholar
Borodin, A. N. and Salminen, P. (2015). Handbook of Brownian Motion: Facts and Formulae, 2nd edn (Probability and Its Applications). Birkhäuser, Basel.Google Scholar
Christensen, S. and Lindensjö, K. (2018). On time-inconsistent stopping problems and mixed strategy stopping times. Available at arXiv:1804.07018.Google Scholar
Chung, K. L. and Walsh, J. B. (2005). Markov Processes, Brownian Motion, and Time Symmetry, 2nd edn (Grundlehren der Mathematischen Wissenschaften 249). Springer, New York.CrossRefGoogle Scholar
Doob, J. L. (1949). Heuristic approach to the Kolmogorov–Smirnov theorems. Ann. Math. Stat. 20, 393–403.CrossRefGoogle Scholar
Fitzsimmons, P., Pitman, J. and Yor, M. (1993). Markovian bridges: construction, Palm interpretation, and splicing. In Seminar on Stochastic Processes (Progress in Probability 32), pp. 101–134. Springer.Google Scholar
Gradshteyn, I. S. and Ryzhik, I. M. (2014). Table of Integrals, Series, and Products, 8th edn. Elsevier/Academic Press, Amsterdam.Google Scholar
Itô, K. and McKean, H. P. (1974). Diffusion Processes and their Sample Paths (Grundlehren der Mathematischen Wissenschaften 125). Springer, Berlin and New York.Google Scholar
Knight, F. B. (1969). Brownian local times and taboo processes. Trans. Amer. Math. Soc. 143, 173–185.CrossRefGoogle Scholar
Kolmogorov, A. N. (1933). Sulla determinazione empirica delle leggi di probabilità. Giorn. Ist. Ital. Attuari 4, 1–11.Google Scholar
Kroese, D., Taimre, T. and Botev, Z. (2011). Handbook of Monte Carlo Methods (Wiley Series in Probability and Statistics). Wiley, New York.Google Scholar
Luoto, A. (2017). Time-dependent weak rate of convergence for functions of generalized bounded variation. Available at arXiv:1609.05768v3.Google Scholar
Pitman, J. and Yor, M. (1999). The law of the maximum of a Bessel bridge. Electron. J. Prob. 4, 1–15.CrossRefGoogle Scholar
Salminen, P. (1997). On last exit decomposition of linear diffusions. Studia Sci. Math. Hungar. 33, 251–262.Google Scholar
Salminen, P. and Yor, M. (2011). On hitting times of affine boundaries by reflecting Brownian motion and Bessel processes. Period. Math. Hungar. 62, 75–101.CrossRefGoogle Scholar
Smirnov, N. V. (1939). On the estimation of the discrepancy between empirical curves of distribution for two independent samples. Bul. Math. de l’Univ. de Moscou 2, 3–14 (in Russian).Google Scholar
Walsh, J. B. (2003). The rate of convergence of the binomial tree scheme. Finance Stoch . 7, 337–361.CrossRefGoogle Scholar