We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
It is known that a bi-orderable group has no generalized torsion element, but the converse does not hold in general. We conjecture that the converse holds for the fundamental groups of 3-manifolds and verify the conjecture for non-hyperbolic, geometric 3-manifolds. We also confirm the conjecture for some infinite families of closed hyperbolic 3-manifolds. In the course of the proof, we prove that each standard generator of the Fibonacci group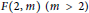 
$F(2,m)\,(m>2)$ is a generalized torsion element.
