Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Teragaito, Masakazu
2020.
Generalized torsion elements and hyperbolic links.
Journal of Knot Theory and Its Ramifications,
Vol. 29,
Issue. 11,
p.
2050079.
Ito, Tetsuya
Motegi, Kimihiko
and
Teragaito, Masakazu
2021.
Generalized torsion and Dehn filling.
Topology and its Applications,
Vol. 301,
Issue. ,
p.
107515.
Motegi, Kimihiko
and
Teragaito, Masakazu
2022.
Generalized torsion for knots with arbitrarily high genus.
Canadian Mathematical Bulletin,
Vol. 65,
Issue. 4,
p.
867.
Himeno, Keisuke
Motegi, Kimihiko
and
Teragaito, Masakazu
2023.
Generalized torsion, unique root property and Baumslag–Solitar relation for knot groups.
Hiroshima Mathematical Journal,
Vol. 53,
Issue. 3,
Himeno, Keisuke
2023.
Complicated generalized torsion elements in Seifert fibered spaces with boundary.
Journal of Knot Theory and Its Ramifications,
Vol. 32,
Issue. 12,
Ito, Tetsuya
Motegi, Kimihiko
and
Teragaito, Masakazu
2023.
Generalized torsion for hyperbolic 3‐manifold groups with arbitrary large rank.
Bulletin of the London Mathematical Society,
Vol. 55,
Issue. 3,
p.
1203.
Bastos, Raimundo
Schneider, Csaba
and
Silveira, Danilo
2024.
Generalized torsion elements in groups.
Archiv der Mathematik,
Vol. 122,
Issue. 2,
p.
121.
Sekino, Nozomu
2024.
Generalized torsion elements in the fundamental groups of once punctured torus bundles.
Topology and its Applications,
Vol. 345,
Issue. ,
p.
108840.
Sekino, Nozomu
2024.
Generalized torsion elements in the fundamental groups of 3-manifolds obtained by 0-surgeries along some double twist knots.
Topology and its Applications,
Vol. 343,
Issue. ,
p.
108798.
Ito, Tetsuya
2025.
Generalized torsion orders and Alexander polynomials.
Canadian Mathematical Bulletin,
p.
1.
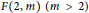 $F(2,m)\,(m>2)$ is a generalized torsion element.
$F(2,m)\,(m>2)$ is a generalized torsion element.

