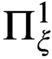1 results
A REFINEMENT OF THE RAMSEY HIERARCHY VIA INDESCRIBABILITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 22 June 2020, pp. 773-808
- Print publication:
- June 2020
-
- Article
- Export citation