 $\mathcal {L}$-invariants and Fontaine–Mazur
$\mathcal {L}$-invariants and Fontaine–Mazur  $\mathcal {L}$-invariants
$\mathcal {L}$-invariants
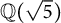 $\mathbb {Q}(\sqrt {\text{5}})$ and
$\mathbb {Q}(\sqrt {\text{5}})$ and 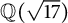 $\mathbb {Q}(\sqrt {\text{17}})$
$\mathbb {Q}(\sqrt {\text{17}})$
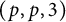 $(p,p,\text{3})$ over number fields
$(p,p,\text{3})$ over number fields
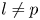 $l \neq p$
$l \neq p$
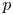 $p$-adic families and
$p$-adic families and 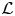 $\mathcal {L}$-invariants
$\mathcal {L}$-invariants
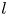 $l$-adic Galois representations, II
$l$-adic Galois representations, II
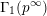 $\unicode[STIX]{x1D6E4}_{1}(p^{\infty })$ and Galois representations
$\unicode[STIX]{x1D6E4}_{1}(p^{\infty })$ and Galois representations