Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T17:01:26.796Z Has data issue: false hasContentIssue false
  • English
  • Français

PATCHING AND THE COMPLETED HOMOLOGY OF LOCALLY SYMMETRIC SPACES

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  27 May 2020

Toby Gee  and
James Newton Open the ORCID record for James Newton [Opens in a new window]
Toby Gee
Affiliation:
Department of Mathematics, Imperial College London, LondonSW7 2AZ, UK ([email protected])
James Newton
Affiliation:
Department of Mathematics, King’s College London, LondonWC2R 2LS, UK ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Under an assumption on the existence of 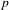$p$-adic Galois representations, we carry out Taylor–Wiles patching (in the derived category) for the completed homology of the locally symmetric spaces associated with 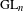$\operatorname{GL}_{n}$ over a number field. We use our construction, and some new results in non-commutative algebra, to show that standard conjectures on completed homology imply ‘big 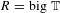$R=\text{big}~\mathbb{T}$’ theorems in situations where one cannot hope to appeal to the Zariski density of classical points (in contrast to all previous results of this kind). In the case where 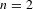$n=2$ and 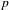$p$ splits completely in the number field, we relate our construction to the 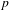$p$-adic local Langlands correspondence for 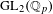$\operatorname{GL}_{2}(\mathbb{Q}_{p})$.

Keywords

Galois representationslocally symmetric spacesp-adic local Langlands

MSC classification

Primary: 11F75: Cohomology of arithmetic groups 11F80: Galois representations
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 2 , March 2022 , pp. 395 - 458
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was supported in part by a Leverhulme Prize, EPSRC grant EP/L025485/1, Marie Curie Career Integration Grant 303605, and by ERC Starting Grant 306326. The second author was supported by ERC Starting Grant 306326.

References

Allen, P. B., On automorphic points in polarized deformation rings, Amer. J. Math. 141(1) (2019), 119–167.CrossRefGoogle Scholar
Allen, P. B., Calegari, F., Caraiani, A., Gee, T., Helm, D., Le Hung, B. V., Newton, J., Scholze, P., Taylor, R. and Thorne, J. A., Potential automorphy over CM fields, Preprint, 2018, arXiv:1812.09999 [math.NT].Google Scholar
Ardakov, K. and Brown, K. A., Ring-theoretic properties of Iwasawa algebras: a survey, Doc. Math. (2006), 7–33; Extra Volume: John H. Coates’ Sixtieth Birthday (special issue).Google Scholar
Ardakov, K. and Brown, K. A., Primeness, semiprimeness and localisation in Iwasawa algebras, Trans. Amer. Math. Soc. 359(4) (2007), 1499–1515.CrossRefGoogle Scholar
Barnet-Lamb, T., Gee, T. and Geraghty, D., Serre weights for rank two unitary groups, Math. Ann. 356(4) (2013), 1551–1598.Google Scholar
Barnet-Lamb, T., Gee, T., Geraghty, D. and Taylor, R., Potential automorphy and change of weight, Ann. of Math. (2) 179(2) (2014), 501–609.CrossRefGoogle Scholar
Barnet-Lamb, T., Geraghty, D., Harris, M. and Taylor, R., A family of Calabi–Yau varieties and potential automorphy II, Publ. Res. Inst. Math. Sci. 47(1) (2011), 29–98.CrossRefGoogle Scholar
Barthel, L. and Livné, R., Irreducible modular representations of GL2 of a local field, Duke Math. J. 75(2) (1994), 261–292.CrossRefGoogle Scholar
Böckle, G., On the density of modular points in universal deformation spaces, Amer. J. Math. 123(5) (2001), 985–1007.CrossRefGoogle Scholar
Bökstedt, M. and Neeman, A., Homotopy limits in triangulated categories, Compos. Math. 86(2) (1993), 209–234.Google Scholar
Borel, A. and Serre, J.-P., Corners and arithmetic groups, Comment. Math. Helv. 48 (1973), 436–491. Avec un appendice: Arrondissement des variétés à coins, par A. Douady et L. Hérault.CrossRefGoogle Scholar
Borel, A. and Wallach, N., Continuous Cohomology, Discrete Subgroups, and Representations of Reductive Groups, 2nd ed., Mathematical Surveys and Monographs, Volume 67, pp. xviii+260 (American Mathematical Society, Providence, RI, 2000).CrossRefGoogle Scholar
Bourbaki, N., Commutative algebra. Chapters 1–7, in Elements of Mathematics (Berlin), pp. xxiv+625 (Springer, Berlin, 1998). Translated from the French, Reprint of the 1989 English translation.Google Scholar
Breuil, C., Sur quelques représentations modulaires et p-adiques de GL2(Q p). I, Compos. Math. 138(2) (2003), 165–188.CrossRefGoogle Scholar
Breuil, C. and Mézard, A., Multiplicités modulaires et représentations de GL2(Z p) et de Gal( Q p/Q p) en l = p , Duke Math. J. 115(2) (2002), 205–310. With an appendix by G. Henniart.Google Scholar
Brumer, A., Pseudocompact algebras, profinite groups and class formations, J. Algebra 4 (1966), 442–470.CrossRefGoogle Scholar
Calegari, F. and Emerton, M., Completed cohomology—a survey, in Non-abelian Fundamental Groups and Iwasawa Theory,London Mathematical Society Lecture Note Series, Volume 393, pp. 239–257 (Cambridge University Press, Cambridge, 2012).Google Scholar
Caraiani, A., Emerton, M., Gee, T., Geraghty, D., Paškūnas, V. and Shin, S. W., Patching and the p-adic local Langlands correspondence, Camb. J. Maths 4(2) (2016), 197–287.CrossRefGoogle Scholar
Caraiani, A., Emerton, M., Gee, T., Geraghty, D., Paškūnas, V. and Shin, S. W., Patching and the p-adic Langlands program for GL2(ℚp), Compos. Math. 154(3) (2018), 503–548.CrossRefGoogle Scholar
Calegari, F. and Geraghty, D., Modularity lifting beyond the Taylor–Wiles method, Invent. Math. 211(1) (2018), 297–433.10.1007/s00222-017-0749-xCrossRefGoogle Scholar
Calegari, F. and Mazur, B., Nearly ordinary Galois deformations over arbitrary number fields, J. Inst. Math. Jussieu 8(1) (2009), 99–177.CrossRefGoogle Scholar
Caraiani, A., Gulotta, D. R., Hsu, C.-Y., Johansson, C., Mocz, L., Reinecke, E. and Shih, S.-C., Shimura varieties at level $\unicode[STIX]{x1D6E4}_{1}(p^{\infty })$ and Galois representations, Compos. Math. (2018), to appear, Preprint, 2018, arXiv:1804.00136 [math.NT].Google Scholar
Caraiani, A. and Le Hung, B. V., On the image of complex conjugation in certain Galois representations, Compos. Math. 152(7) (2016), 1476–1488.CrossRefGoogle Scholar
Caraiani, A. and Scholze, P., On the generic part of the cohomology of compact unitary Shimura varieties, Ann. of Math. (2) 186(3) (2017), 649–766.CrossRefGoogle Scholar
Chenevier, G., On the infinite fern of Galois representations of unitary type, Ann. Sci. Éc. Norm. Supér. (4) 44(6) (2011), 963–1019.CrossRefGoogle Scholar
Clozel, L., Harris, M. and Taylor, R., Automorphy for some l-adic lifts of automorphic mod l Galois representations, Publ. Math. Inst. Haute Études Sci. 108 (2008), 1–181.CrossRefGoogle Scholar
Colmez, P., Représentations de GL2(Q p) et (𝜙, 𝛤)-modules, Astérisque 330 (2010), 281–509.Google Scholar
Colmez, P., Dospinescu, G. and Paškūnas, V., The p-adic local Langlands correspondence for GL2(ℚp), Camb. J. Math. 2(1) (2014), 1–47.CrossRefGoogle Scholar
Diamond, F., An extension of Wiles’ results, in Modular Forms and Fermat’s Last Theorem (Boston, MA, 1995), pp. 475–489 (Springer, New York, 1997).10.1007/978-1-4612-1974-3_17CrossRefGoogle Scholar
Emerton, M., Ordinary parts of admissible representations of p-adic reductive groups I. Definition and first properties, Astérisque 331 (2010), 355–402.Google Scholar
Emerton, M., Ordinary parts of admissible representations of p-adic reductive groups II. Derived functors, Astérisque 331 (2010), 403–459.Google Scholar
Emerton, M., Completed cohomology and the p-adic Langlands program, in Proceedings of the International Congress of Mathematicians, 2014, Volume II, pp. 319–342 (Kyung Moon Sa, Seoul, 2014).Google Scholar
Emerton, M., Local-global compatibility in the $p$ -adic Langlands programme for $\text{GL}_{2}/\mathbb{Q}$ (2010), available at http://www.math.uchicago.edu/∼emerton/pdffiles/lg.pdf.Google Scholar
Emerton, M. and Paskunas, V., On the density of supercuspidal points of fixed weight in local deformation rings and global Hecke algebras, Journal de l’École polytechnique Mathématiques 7 (2020), 337–371.CrossRefGoogle Scholar
Foxby, H.-B. and Iyengar, S., Depth and amplitude for unbounded complexes, in Commutative Algebra (Grenoble/Lyon, 2001), Volume 331, pp. 119–137 (Contemporary Mathematics American Mathematical Society, Providence, RI, 2003).CrossRefGoogle Scholar
Galatius, S. and Venkatesh, A., Derived Galois deformation rings, Adv. Maths 327 (2018), 470–623.CrossRefGoogle Scholar
Gouvêa, F. Q. and Mazur, B., On the density of modular representations, in Computational Perspectives on Number Theory (Chicago, IL, 1995), Volume 7, pp. 127–142 (American Mathematical Society/IP Stud. Adv. Math. American Mathematical Society, Providence, RI, 1998).CrossRefGoogle Scholar
Grothendieck, A., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. I, Publ. Math. Inst. Hautes Études Sci. 20 (1964), 5-259.10.1007/BF02684747CrossRefGoogle Scholar
Hansen, D., Minimal modularity lifting for $\text{GL}_{2}$ over an arbitrary number field, ArXiv e-prints (Sept. 2012), Math. Res. Lett. (2012), to appear, arXiv:1209.5309 [math.NT].Google Scholar
Iyengar, S., Depth for complexes, and intersection theorems, Math. Z. 230(3) (1999), 545–567.10.1007/PL00004705CrossRefGoogle Scholar
Khare, C. B. and Thorne, J. A., Potential automorphy and the Leopoldt conjecture, Amer. J. Maths 139(5) (2017), 1205–1273.10.1353/ajm.2017.0030CrossRefGoogle Scholar
Kisin, M., Potentially semi-stable deformation rings, J. Amer. Math. Soc. 21(2) (2008), 513–546.CrossRefGoogle Scholar
Lazard, M., Groupes analytiques p-adiques, Publ. Math. Inst. Hautes Études Sci. 26 (1965), 389–603.Google Scholar
Levasseur, T., Some properties of noncommutative regular graded rings, Glasg. Math. J. 34(3) (1992), 277–300.CrossRefGoogle Scholar
Li, H. and van Oystaeyen, F., Zariskian Filtrations, K-Monographs in Mathematics, Volume 2, pp. x+252 (Kluwer Academic Publishers, Dordrecht, 1996).Google Scholar
Matsumura, H., Commutative Ring Theory, 2nd ed., Cambridge Studies in Advanced Mathematics, Volume 8, pp. xiv+320 (Cambridge University Press, Cambridge, 1989). Translated from the Japanese by M. Reid.Google Scholar
Mumford, D., Abelian Varieties, Tata Institute of Fundamental Research Studies in Mathematics, Volume 5, pp. xii+263 (Hindustan Book Agency, New Delhi, 2008). With appendices by C. P. Ramanujam and Y. Manin, Corrected reprint of the 2nd ed. (1974).Google Scholar
Newton, J. and Thorne, J. A., Torsion Galois representations over CM fields and Hecke algebras in the derived category, Forum Math. Sigma 4 (2016), e21, 88.CrossRefGoogle Scholar
Paškūnas, V., The image of Colmez’s Montreal functor, Publ. Math. Inst. Hautes Études Sci. 118 (2013), 1–191.CrossRefGoogle Scholar
Paškūnas, V., On the Breuil–Mézard conjecture, Duke Math. J. 164(2) (2015), 297–359.CrossRefGoogle Scholar
Persiflage, The thick diagonal, Blog post at http://galoisrepresentations.wordpress.com/2014/03/14/the-thick-diagonal/.Google Scholar
Raghunathan, M. S., A note on quotients of real algebraic groups by arithmetic subgroups, Invent. Math. 4 (1967/1968), 318–335.CrossRefGoogle Scholar
Roberts, P., Homological Invariants of Modules Over Commutative Rings, Séminaire de Mathématiques Supérieures [Seminar on Higher Mathematics], Volume 72, p. 110 (Presses de l’Université de Montréal, Montreal, Quebec, 1980).Google Scholar
Scholze, P., On torsion in the cohomology of locally symmetric varieties, Ann. of Math. (2) 182(3) (2015), 945–1066.CrossRefGoogle Scholar
Scholze, P., On the p-adic cohomology of the Lubin–Tate tower, Ann. Sci. Éc. Norm. Supér. (4) 51(4) (2018), 811–863. With an appendix by M. Rapoport.CrossRefGoogle Scholar
Schmidt, T. and Strauch, M., Dimensions of some locally analytic representations, Represent. Theory 20 (2016), 14–38.10.1090/ert/475CrossRefGoogle Scholar
Serre, J.-P., Sur la dimension cohomologique des groupes profinis, Topology 3 (1965), 413–420.CrossRefGoogle Scholar
Shotton, J., The Breuil–Mézard conjecture when l≠p , Duke Math. J. 167(4) (2018), 603–678.CrossRefGoogle Scholar
The Stacks Project Authors, Stacks Project. http://stacks.math.columbia.edu. 2013.Google Scholar
Sweedler, M. E., Preservation of flatness for the product of modules over the product of rings, J. Algebra 74(1) (1982), 159–205.CrossRefGoogle Scholar
Taylor, R., Automorphy for some l-adic lifts of automorphic mod l Galois representations. II, Publ. Math. Inst. Hautes Études Sci. 108 (2008), 183–239.CrossRefGoogle Scholar
Thorne, J., On the automorphy of l-adic Galois representations with small residual image, J. Inst. Math. Jussieu 11(4) (2012), 855–920. With an appendix by R. Guralnick, F. Herzig, R. Taylor and Thorne.CrossRefGoogle Scholar
Venjakob, O., On the structure theory of the Iwasawa algebra of a p-adic Lie group, J. Eur. Math. Soc. (JEMS) 4(3) (2002), 271–311.CrossRefGoogle Scholar
Wadsley, S., A Bernstein-type inequality for localizations of Iwasawa algebras of Heisenberg pro-p groups, Q. J. Math. 58(2) (2007), 265–277.CrossRefGoogle Scholar
Weibel, C. A., An Introduction to Homological Algebra, Cambridge Studies in Advanced Mathematics, Volume 38, pp. xiv+450 (Cambridge University Press, Cambridge, 1994).CrossRefGoogle Scholar