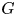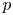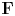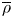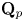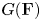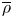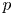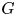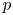1. Introduction
1.1 Crystalline deformation rings
Let ![]() $p$ be a prime, and let
$p$ be a prime, and let ![]() $\Lambda$ be the ring of integers in a
$\Lambda$ be the ring of integers in a ![]() $p$-adic field
$p$-adic field ![]() $L$ with residue field
$L$ with residue field ![]() $\mathbf {F}$. We fix a split reductive group
$\mathbf {F}$. We fix a split reductive group ![]() $G$ over
$G$ over ![]() $\Lambda$. Then let
$\Lambda$. Then let ![]() $K$ be a
$K$ be a ![]() $p$-adic field unramified over
$p$-adic field unramified over ![]() $\mathbf {Q}_{p}$ with residue field
$\mathbf {Q}_{p}$ with residue field ![]() $k$ and ring of integers
$k$ and ring of integers ![]() $W(k)$, and denote the absolute Galois group of
$W(k)$, and denote the absolute Galois group of ![]() $K$ by
$K$ by ![]() $\Gamma _K$.
$\Gamma _K$.
For a fixed continuous homomorphism ![]() ${\overline {\rho }}: \Gamma _K \to G(\mathbf {F})$, there has been considerable interest in studying lifts of
${\overline {\rho }}: \Gamma _K \to G(\mathbf {F})$, there has been considerable interest in studying lifts of ![]() ${\overline {\rho }}$ with ‘nice’ properties, in particular lifts closely connected to
${\overline {\rho }}$ with ‘nice’ properties, in particular lifts closely connected to ![]() $p$-adic Hodge theory. This began with Ramakrishna's results on flat deformations [Reference RamakrishnaRam93], which played an important role in the Taylor–Wiles proof of modularity of semistable elliptic curves over
$p$-adic Hodge theory. This began with Ramakrishna's results on flat deformations [Reference RamakrishnaRam93], which played an important role in the Taylor–Wiles proof of modularity of semistable elliptic curves over ![]() $\mathbf {Q}$. Most automorphy lifting theorems for
$\mathbf {Q}$. Most automorphy lifting theorems for ![]() $\operatorname {GL}_n$ use either an ordinary or Fontaine–Laffaille condition at
$\operatorname {GL}_n$ use either an ordinary or Fontaine–Laffaille condition at ![]() $p$ to ensure that the local deformation ring is nice. Fontaine–Laffaille theory [Reference Fontaine and LaffailleFL82] lets one study special cases of the crystalline deformation rings for
$p$ to ensure that the local deformation ring is nice. Fontaine–Laffaille theory [Reference Fontaine and LaffailleFL82] lets one study special cases of the crystalline deformation rings for ![]() $G = \operatorname {GL}_n$ constructed by Kisin [Reference KisinKis08] when
$G = \operatorname {GL}_n$ constructed by Kisin [Reference KisinKis08] when ![]() $p$ is unramified in
$p$ is unramified in ![]() $K$ and the Hodge–Tate weights lie in a small interval relative to
$K$ and the Hodge–Tate weights lie in a small interval relative to ![]() $p$. In this paper, we address the natural question of finding an analogue of the Fontaine–Laffaille condition for
$p$. In this paper, we address the natural question of finding an analogue of the Fontaine–Laffaille condition for ![]() $G$-valued crystalline deformations. More precisely, we give a root theoretic condition on the Hodge–Tate cocharacter which ensures that the crystalline deformation ring is formally smooth. Up to technical conditions on the isogeny class of the group
$G$-valued crystalline deformations. More precisely, we give a root theoretic condition on the Hodge–Tate cocharacter which ensures that the crystalline deformation ring is formally smooth. Up to technical conditions on the isogeny class of the group ![]() $G$, we believe this result is close to optimal when the cocharacter is regular. As discussed in the following, our result improves on all known results for classical groups not of type A and provides the first such results for exceptional groups.
$G$, we believe this result is close to optimal when the cocharacter is regular. As discussed in the following, our result improves on all known results for classical groups not of type A and provides the first such results for exceptional groups.
We begin by stating our result more precisely. If ![]() $B$ is an
$B$ is an ![]() $L$-algebra, a continuous representation of
$L$-algebra, a continuous representation of ![]() $\Gamma _K$ valued in
$\Gamma _K$ valued in ![]() $G(B)$ is crystalline if the composition with any representation of
$G(B)$ is crystalline if the composition with any representation of ![]() $G$ is crystalline. Assuming that
$G$ is crystalline. Assuming that ![]() $\Lambda$ contains a copy of
$\Lambda$ contains a copy of ![]() $W(k)$, to such a representation we may associate a
$W(k)$, to such a representation we may associate a ![]() $p$-adic Hodge type, which is a collection of geometric conjugacy classes of cocharacters of
$p$-adic Hodge type, which is a collection of geometric conjugacy classes of cocharacters of ![]() $G$ indexed by the set
$G$ indexed by the set ![]() $\mathcal {J}$ of embeddings of
$\mathcal {J}$ of embeddings of ![]() $W(k)$ into
$W(k)$ into ![]() $\Lambda$. This generalizes the notation of (labeled) Hodge–Tate weights of a representation of
$\Lambda$. This generalizes the notation of (labeled) Hodge–Tate weights of a representation of ![]() $\Gamma _K$ valued in
$\Gamma _K$ valued in ![]() $\operatorname {GL}_n(B)$.
$\operatorname {GL}_n(B)$.
Let ![]() $\mu = (\mu _{\sigma }) _{\sigma \in \mathcal {J}}$ be a collection of dominant cocharacters of
$\mu = (\mu _{\sigma }) _{\sigma \in \mathcal {J}}$ be a collection of dominant cocharacters of ![]() $G$. Our primary goal is to study the framed crystalline deformation ring with
$G$. Our primary goal is to study the framed crystalline deformation ring with ![]() $p$-adic Hodge type
$p$-adic Hodge type ![]() $\mu$, whose
$\mu$, whose ![]() $L$-points are crystalline representations with
$L$-points are crystalline representations with ![]() $p$-adic Hodge type given by
$p$-adic Hodge type given by ![]() $\mu$. We denote this
$\mu$. We denote this ![]() $\Lambda$-algebra by
$\Lambda$-algebra by ![]() $R_{{\overline {\rho }}}^{\mu,\square }$.
$R_{{\overline {\rho }}}^{\mu,\square }$.
Definition 1.1.1 We say that ![]() $\mu$ is Fontaine–Laffaille, or lies in the Fontaine–Laffaille range, provided that
$\mu$ is Fontaine–Laffaille, or lies in the Fontaine–Laffaille range, provided that ![]() $\langle \mu _\sigma,\alpha \rangle < p-1$ for every root
$\langle \mu _\sigma,\alpha \rangle < p-1$ for every root ![]() $\alpha \in \Phi _{G}$ and every embedding
$\alpha \in \Phi _{G}$ and every embedding ![]() $\sigma$ of
$\sigma$ of ![]() $W(k)$ into
$W(k)$ into ![]() $L$. We say
$L$. We say ![]() $\mu$ is strongly Fontaine–Laffaille provided that
$\mu$ is strongly Fontaine–Laffaille provided that ![]() $\langle \mu _\sigma,\alpha \rangle < ({p-1})/{2}$ for every root
$\langle \mu _\sigma,\alpha \rangle < ({p-1})/{2}$ for every root ![]() $\alpha \in \Phi _{G}$ and every embedding.
$\alpha \in \Phi _{G}$ and every embedding.
There is a natural way to associate potential ![]() $p$-adic Hodge types
$p$-adic Hodge types ![]() $\mu$ to
$\mu$ to ![]() ${\overline {\rho }}$.
${\overline {\rho }}$.
Theorem A Suppose ![]() $p$ is unramified in
$p$ is unramified in ![]() $K$ and that
$K$ and that ![]() $p \nmid \# \pi _1(G^{\mathrm {ad}})$, where
$p \nmid \# \pi _1(G^{\mathrm {ad}})$, where ![]() $G^{\mathrm {ad}}$ is the adjoint group of
$G^{\mathrm {ad}}$ is the adjoint group of ![]() $G$. Fix a Galois representation
$G$. Fix a Galois representation ![]() ${\overline {\rho }} : \Gamma _K \to G(\mathbf {F})$ and a potential
${\overline {\rho }} : \Gamma _K \to G(\mathbf {F})$ and a potential ![]() $p$-adic Hodge type
$p$-adic Hodge type ![]() $\mu$ for the representation.Footnote 1 If
$\mu$ for the representation.Footnote 1 If ![]() $\operatorname {Spf} R_{{\overline {\rho }}}^{\mu,\square }$ is non-empty and either:
$\operatorname {Spf} R_{{\overline {\rho }}}^{\mu,\square }$ is non-empty and either:
(i)
 $\mu$ is Fontaine–Laffaille and the derived group
$\mu$ is Fontaine–Laffaille and the derived group  $G^{\operatorname {der}}$ is simply connected; or
$G^{\operatorname {der}}$ is simply connected; or(ii)
 $\mu$ is strongly Fontaine–Laffaille;
$\mu$ is strongly Fontaine–Laffaille;
then ![]() $\operatorname {Spf} R_{{\overline {\rho }}}^{\mu,\square }$ is formally smooth over
$\operatorname {Spf} R_{{\overline {\rho }}}^{\mu,\square }$ is formally smooth over ![]() $\operatorname {Spf}(\Lambda )$.
$\operatorname {Spf}(\Lambda )$.
Remark 1.1.2 If ![]() $\operatorname {Spf} R_{{\overline {\rho }}}^{\mu,\square }$ is non-empty, its dimension is
$\operatorname {Spf} R_{{\overline {\rho }}}^{\mu,\square }$ is non-empty, its dimension is ![]() $\dim G_\mathbf {F} + \sum _{\sigma \in \mathcal {J}} \dim P_{\mu _{\sigma },\mathbf {F}} \backslash G_\mathbf {F}$ where
$\dim G_\mathbf {F} + \sum _{\sigma \in \mathcal {J}} \dim P_{\mu _{\sigma },\mathbf {F}} \backslash G_\mathbf {F}$ where ![]() $P_{\mu _{\sigma },\mathbf {F}}$ is the parabolic associated to
$P_{\mu _{\sigma },\mathbf {F}}$ is the parabolic associated to ![]() $\mu _{\sigma }$; this follows from studying the generic fiber [Reference BalajiBal12, Theorem 5.1.5]. The assumption that
$\mu _{\sigma }$; this follows from studying the generic fiber [Reference BalajiBal12, Theorem 5.1.5]. The assumption that ![]() $\operatorname {Spf} R_{{\overline {\rho }}}^{\mu,\square }$ is non-empty is harmless in many applications, for example to modularity lifting theorems. Furthermore, when
$\operatorname {Spf} R_{{\overline {\rho }}}^{\mu,\square }$ is non-empty is harmless in many applications, for example to modularity lifting theorems. Furthermore, when ![]() $\mu$ is regular, one does not need the assumption that
$\mu$ is regular, one does not need the assumption that ![]() $\mu$ is a potential
$\mu$ is a potential ![]() $p$-adic Hodge type; the assumption that
$p$-adic Hodge type; the assumption that ![]() $\operatorname {Spf} R_{{\overline {\rho }}}^{\mu,\square }$ is non-empty suffices (see Remark 6.4.5).
$\operatorname {Spf} R_{{\overline {\rho }}}^{\mu,\square }$ is non-empty suffices (see Remark 6.4.5).
Theorem A generalizes previous results about crystalline deformation rings obtained using Fontaine–Laffaille theory for the general linear, symplectic, and orthogonal groups. Beyond these cases, for example for spin and exceptional groups, it provides completely new information.
Example 1.1.3 When ![]() $G = \operatorname {GL}_n$, the condition that
$G = \operatorname {GL}_n$, the condition that ![]() $\mu$ is Fontaine–Laffaille is equivalent to the Hodge–Tate weights of the
$\mu$ is Fontaine–Laffaille is equivalent to the Hodge–Tate weights of the ![]() $p$-adic Hodge type (using the standard representation) lying in an interval of length less than
$p$-adic Hodge type (using the standard representation) lying in an interval of length less than ![]() $p-1$ for each embedding of
$p-1$ for each embedding of ![]() $L$ into
$L$ into ![]() $K$. In this situation, Clozel, Harris, and Taylor applied Fontaine–Laffaille theory to show formal smoothness of the Fontaine–Laffaille deformation ring [Reference Clozel, Harris and TaylorCHT08, § 2.4]. This deformation ring is none other than the crystalline deformation ring we consider. Our proof uses the theory of Kisin modules and so is independent of Fontaine–Laffaille theory. Theorem A has an extra hypothesis, that
$K$. In this situation, Clozel, Harris, and Taylor applied Fontaine–Laffaille theory to show formal smoothness of the Fontaine–Laffaille deformation ring [Reference Clozel, Harris and TaylorCHT08, § 2.4]. This deformation ring is none other than the crystalline deformation ring we consider. Our proof uses the theory of Kisin modules and so is independent of Fontaine–Laffaille theory. Theorem A has an extra hypothesis, that ![]() $p \nmid n = \# \pi _1(\operatorname {PGL}_n)$. This hypothesis is needed to apply Proposition 5.1.1, where it is used to reduce to the adjoint case. For the special case of
$p \nmid n = \# \pi _1(\operatorname {PGL}_n)$. This hypothesis is needed to apply Proposition 5.1.1, where it is used to reduce to the adjoint case. For the special case of ![]() $G=\operatorname {GL}_n$, it is not hard to do a direct analysis and remove this hypothesis (see Remark 5.1.3).
$G=\operatorname {GL}_n$, it is not hard to do a direct analysis and remove this hypothesis (see Remark 5.1.3).
Example 1.1.4 When ![]() $p \neq 2$, we can apply Theorem A to symplectic and orthogonal groups. Now
$p \neq 2$, we can apply Theorem A to symplectic and orthogonal groups. Now ![]() $\operatorname {Sp}_{2n}$ is simply connected while
$\operatorname {Sp}_{2n}$ is simply connected while ![]() $\operatorname {SO}_n$ is not, and the highest roots (using the standard descriptions of the root system) are
$\operatorname {SO}_n$ is not, and the highest roots (using the standard descriptions of the root system) are ![]() $2e_1$ and
$2e_1$ and ![]() $e_1+e_2$, respectively. Using the standard representation, we can relate
$e_1+e_2$, respectively. Using the standard representation, we can relate ![]() $p$-adic Hodge types to Hodge–Tate weights. We see that our result applies to
$p$-adic Hodge types to Hodge–Tate weights. We see that our result applies to ![]() $\operatorname {Sp}_{2n}$ for Fontaine–Laffaille
$\operatorname {Sp}_{2n}$ for Fontaine–Laffaille ![]() $\mu$, when the Hodge–Tate weights of the
$\mu$, when the Hodge–Tate weights of the ![]() $p$-adic Hodge type lie in the open interval
$p$-adic Hodge type lie in the open interval ![]() $(- ({p-1})/{2}, ({p-1})/{2})$ for each embedding of
$(- ({p-1})/{2}, ({p-1})/{2})$ for each embedding of ![]() $L$ into
$L$ into ![]() $K$. There is an obvious extension to
$K$. There is an obvious extension to ![]() $\operatorname {GSp}_{2n}$ with Hodge–Tate weights lying in an interval of length less than
$\operatorname {GSp}_{2n}$ with Hodge–Tate weights lying in an interval of length less than ![]() $p-1$.
$p-1$.
Similarly, our results apply to ![]() $\operatorname {SO}_n$ for strongly Fontaine–Laffaille
$\operatorname {SO}_n$ for strongly Fontaine–Laffaille ![]() $\mu$, when the sum of the two largest Hodge–Tate weights is less than
$\mu$, when the sum of the two largest Hodge–Tate weights is less than ![]() $ ({p-1})/{4}$ for each embedding of
$ ({p-1})/{4}$ for each embedding of ![]() $L$ into
$L$ into ![]() $K$. This is the case, for example, if the Hodge–Tate weights lie in
$K$. This is the case, for example, if the Hodge–Tate weights lie in ![]() $(- ({p-1})/{4}, ({p-1})/{4})$.
$(- ({p-1})/{4}, ({p-1})/{4})$.
This generalizes results of Patrikis and the first author (see [Reference PatrikisPat06] and [Reference BooherBoo19, Theorem 5.2]) which use Fontaine–Laffaille modules with pairings to show formal smoothness under the additional assumption that the Hodge–Tate weights with respect to the standard embedding lie in an interval of length less than ![]() $(p-1)/2$ (for each embedding of
$(p-1)/2$ (for each embedding of ![]() $L$ into
$L$ into ![]() $K$) and that the
$K$) and that the ![]() $p$-adic Hodge type is regular (i.e. for each embedding the Hodge–Tate weights are distinct). In the symplectic case, our method gives roughly double the range of Hodge–Tate weights, while we obtain a similar range for special orthogonal groups but with some added flexibility involving the second-largest Hodge–Tate weight.
$p$-adic Hodge type is regular (i.e. for each embedding the Hodge–Tate weights are distinct). In the symplectic case, our method gives roughly double the range of Hodge–Tate weights, while we obtain a similar range for special orthogonal groups but with some added flexibility involving the second-largest Hodge–Tate weight.
Example 1.1.5 As spin groups are simply connected, Theorem A applies to Fontaine–Laffaille ![]() $p$-adic Hodge types. Under the quotient map
$p$-adic Hodge types. Under the quotient map ![]() $\operatorname {Spin}_n \to \operatorname {SO}_n$ and embedding
$\operatorname {Spin}_n \to \operatorname {SO}_n$ and embedding ![]() $\operatorname {SO}_n \hookrightarrow \operatorname {GL}_n$, this implies the sum of the two largest Hodge–Tate weights would be less than
$\operatorname {SO}_n \hookrightarrow \operatorname {GL}_n$, this implies the sum of the two largest Hodge–Tate weights would be less than ![]() $p-1$.
$p-1$.
If we attempted to deduce things about the crystalline deformation ring for ![]() $\operatorname {Spin}_n$-valued representations via the quotient map
$\operatorname {Spin}_n$-valued representations via the quotient map ![]() $\operatorname {Spin}_n \to \operatorname {SO}_n$ and applying Fontaine–Laffaille theory with pairings to study
$\operatorname {Spin}_n \to \operatorname {SO}_n$ and applying Fontaine–Laffaille theory with pairings to study ![]() $\operatorname {SO}_n$-valued representations, we would need a much stronger condition, that the largest Hodge–Tate weight is less than
$\operatorname {SO}_n$-valued representations, we would need a much stronger condition, that the largest Hodge–Tate weight is less than ![]() $ ({p-1})/{4}$.
$ ({p-1})/{4}$.
Remark 1.1.6 When ![]() $G^{\operatorname {der}}$ is not simply connected, the hypothesis that
$G^{\operatorname {der}}$ is not simply connected, the hypothesis that ![]() $\mu$ is strongly Fontaine–Laffaille and not just Fontaine–Laffaille is necessary, even though it might not be initially expected. Example 6.2.4 gives an example of a representations
$\mu$ is strongly Fontaine–Laffaille and not just Fontaine–Laffaille is necessary, even though it might not be initially expected. Example 6.2.4 gives an example of a representations ![]() $\rho$ valued in
$\rho$ valued in ![]() $\operatorname {GL}_2$ with quotient
$\operatorname {GL}_2$ with quotient ![]() $\rho '$ valued in
$\rho '$ valued in ![]() $\operatorname {PGL}_2$ with associated Hodge–Tate weights
$\operatorname {PGL}_2$ with associated Hodge–Tate weights ![]() $0$ and
$0$ and ![]() $ ({p-1})/{2}$. This is Fontaine–Laffaille but not strongly Fontaine–Laffaille. Our result shows the crystalline deformation ring for
$ ({p-1})/{2}$. This is Fontaine–Laffaille but not strongly Fontaine–Laffaille. Our result shows the crystalline deformation ring for ![]() $\rho$ is formally smooth, but does not apply for
$\rho$ is formally smooth, but does not apply for ![]() $\rho '$. We do not expect the deformation ring for
$\rho '$. We do not expect the deformation ring for ![]() $\rho '$ to be smooth.
$\rho '$ to be smooth.
The group ![]() $G^{\operatorname {der}}$ being simply connected or
$G^{\operatorname {der}}$ being simply connected or ![]() $\mu$ being strongly Fontaine–Laffaille is actually a proxy for a more technical condition (the Kisin variety being trivial, see Theorem 6.4.4) which we expect to hold for most
$\mu$ being strongly Fontaine–Laffaille is actually a proxy for a more technical condition (the Kisin variety being trivial, see Theorem 6.4.4) which we expect to hold for most ![]() ${\overline {\rho }}$ when
${\overline {\rho }}$ when ![]() $\mu$ is Fontaine–Laffaille even if
$\mu$ is Fontaine–Laffaille even if ![]() $G^{\operatorname {der}}$ is not simply connected.
$G^{\operatorname {der}}$ is not simply connected.
Remark 1.1.7 The condition that ![]() $p \nmid \# \pi _1(G^{\mathrm {ad}})$ in Theorem A is actually two conditions: the center of
$p \nmid \# \pi _1(G^{\mathrm {ad}})$ in Theorem A is actually two conditions: the center of ![]() $G^{\operatorname {der}}$ is prime to
$G^{\operatorname {der}}$ is prime to ![]() $p$ order and
$p$ order and ![]() $p \nmid \# \pi _1(G^{\operatorname {der}})$ where
$p \nmid \# \pi _1(G^{\operatorname {der}})$ where ![]() $G^{\operatorname {der}}$ is the derived group of
$G^{\operatorname {der}}$ is the derived group of ![]() $G$. The former only appears in a tangent space estimate (Proposition 5.1.1) and can likely be removed. The latter condition arises out of serious technical issues with the theory of mixed characteristic affine Schubert varieties for these groups. We do not know if this condition can be removed.
$G$. The former only appears in a tangent space estimate (Proposition 5.1.1) and can likely be removed. The latter condition arises out of serious technical issues with the theory of mixed characteristic affine Schubert varieties for these groups. We do not know if this condition can be removed.
Finally, we discuss the condition that ![]() $R_{\overline {\rho }}^{\mu,\square }$ is non-empty, or equivalently that
$R_{\overline {\rho }}^{\mu,\square }$ is non-empty, or equivalently that ![]() ${\overline {\rho }}$ admits a crystalline lift with
${\overline {\rho }}$ admits a crystalline lift with ![]() $p$-adic Hodge type
$p$-adic Hodge type ![]() $\mu$. As discussed in § 1.2, our primary analysis is in characteristic
$\mu$. As discussed in § 1.2, our primary analysis is in characteristic ![]() $p$. We expect proving the existence of crystalline lifts with particular
$p$. We expect proving the existence of crystalline lifts with particular ![]() $p$-adic Hodge type to require unrelated techniques, and so are content to assume the existence of a lift in Theorem A. This is not an issue for applications to automorphy lifting where a lift is often given. However, it is a manner in which our methods are weaker than usual Fontaine–Laffaille theory. Given that
$p$-adic Hodge type to require unrelated techniques, and so are content to assume the existence of a lift in Theorem A. This is not an issue for applications to automorphy lifting where a lift is often given. However, it is a manner in which our methods are weaker than usual Fontaine–Laffaille theory. Given that ![]() ${\overline {\rho }}$ admits a lift of type
${\overline {\rho }}$ admits a lift of type ![]() $\mu$ (i.e.
$\mu$ (i.e. ![]() $\operatorname {Spf} R^{\mu, \square }_{{\overline {\rho }}}$ is non-empty), Levin [Reference LevinLev15] showed that there is a
$\operatorname {Spf} R^{\mu, \square }_{{\overline {\rho }}}$ is non-empty), Levin [Reference LevinLev15] showed that there is a ![]() $G$-Kisin module
$G$-Kisin module ![]() $(\mathfrak {P}, \phi _{\mathfrak {P}})$ with coefficients in
$(\mathfrak {P}, \phi _{\mathfrak {P}})$ with coefficients in ![]() $\mathbf {F}$ giving rise to
$\mathbf {F}$ giving rise to ![]() ${\overline {\rho }}|_{\Gamma _\infty }$, and the conditions in the theorem ensure that
${\overline {\rho }}|_{\Gamma _\infty }$, and the conditions in the theorem ensure that ![]() $\mathfrak {P}$ is unique. Furthermore, the elementary divisors of
$\mathfrak {P}$ is unique. Furthermore, the elementary divisors of ![]() $\phi _{\mathfrak {P}}$ (with respect to variable
$\phi _{\mathfrak {P}}$ (with respect to variable ![]() $u$ and decomposed over embeddings of
$u$ and decomposed over embeddings of ![]() $W(k)$ into
$W(k)$ into ![]() $\Lambda$) are given by dominant cocharacters
$\Lambda$) are given by dominant cocharacters ![]() $\mu ' = (\mu '_\sigma )_{\sigma \in \mathcal {J}}$ such that
$\mu ' = (\mu '_\sigma )_{\sigma \in \mathcal {J}}$ such that ![]() $\mu '_\sigma \leqslant \mu _\sigma$ in the Bruhat order. We call
$\mu '_\sigma \leqslant \mu _\sigma$ in the Bruhat order. We call ![]() $\mu '$ the shape of
$\mu '$ the shape of ![]() $\mathfrak {P}$. The condition that
$\mathfrak {P}$. The condition that ![]() $\mu$ is a potential
$\mu$ is a potential ![]() $p$-adic Hodge type in Theorem A is that
$p$-adic Hodge type in Theorem A is that ![]() $\mu ' = \mu$. The theorem we prove in § 6 is more general than this, for example, if we assume that
$\mu ' = \mu$. The theorem we prove in § 6 is more general than this, for example, if we assume that ![]() $\mu$ is regular then the assumption that
$\mu$ is regular then the assumption that ![]() $\mu ' = \mu$ is not necessary as long as we assume existence of a lift (see Remark 6.4.5).
$\mu ' = \mu$ is not necessary as long as we assume existence of a lift (see Remark 6.4.5).
If ![]() ${\overline {\rho }}$ is tamely ramified such that the image of
${\overline {\rho }}$ is tamely ramified such that the image of ![]() ${\overline {\rho }}$ lies in the normalizer of a maximal torus
${\overline {\rho }}$ lies in the normalizer of a maximal torus ![]() $T \subset G$, it is often possible in a combinatorial way to construct crystalline lifts of specified
$T \subset G$, it is often possible in a combinatorial way to construct crystalline lifts of specified ![]() $\mu$ which are also similarly valued in the normalizer of
$\mu$ which are also similarly valued in the normalizer of ![]() $T$. These are often referred to as obvious or explicit crystalline lifts and give a class of
$T$. These are often referred to as obvious or explicit crystalline lifts and give a class of ![]() ${\overline {\rho }}$ to which our theorem applies. The combinatorics of these lifts for a general group
${\overline {\rho }}$ to which our theorem applies. The combinatorics of these lifts for a general group ![]() $G$ is explored to some extent in Gee, Herzig, and Savitt [Reference Gee, Herzig and SavittGHS18] in the context of the weight part of Serre's conjecture.
$G$ is explored to some extent in Gee, Herzig, and Savitt [Reference Gee, Herzig and SavittGHS18] in the context of the weight part of Serre's conjecture.
Lin has also recently investigated the existence of crystalline lifts [Reference LinLin21, Reference LinLin22].
Remark 1.1.8 Although we have not attempted to prove it here, our expectation is that if ![]() ${\overline {\rho }}$ admits a lift of type
${\overline {\rho }}$ admits a lift of type ![]() $\mu$, then the shape of
$\mu$, then the shape of ![]() $\mathfrak {P}$ must be exactly
$\mathfrak {P}$ must be exactly ![]() $\mu$ rather than strictly smaller. This is consistent with the fact that Fontaine–Laffaille modules only deform in fixed weight for
$\mu$ rather than strictly smaller. This is consistent with the fact that Fontaine–Laffaille modules only deform in fixed weight for ![]() $\operatorname {GL}_n$.
$\operatorname {GL}_n$.
Remark 1.1.9 It is not clear whether an alternate approach using a theory of Fontaine–Laffaille modules with ![]() $G$-structure could be used to prove Theorem A. The advantage of this approach would be that it would also produce a crystalline lift, showing that the crystalline deformation ring is non-empty. While the category of Fontaine–Laffaille modules is a tensor category, the functor relating Galois representations and Fontaine–Laffaille modules has limited compatibility with tensor products. In particular, for Fontaine–Laffaille modules
$G$-structure could be used to prove Theorem A. The advantage of this approach would be that it would also produce a crystalline lift, showing that the crystalline deformation ring is non-empty. While the category of Fontaine–Laffaille modules is a tensor category, the functor relating Galois representations and Fontaine–Laffaille modules has limited compatibility with tensor products. In particular, for Fontaine–Laffaille modules ![]() $M_1$ and
$M_1$ and ![]() $M_2$ the Galois representation associated to
$M_2$ the Galois representation associated to ![]() $M_1 \otimes M_2$ can be shown to be the tensor product of the Galois representations associated to
$M_1 \otimes M_2$ can be shown to be the tensor product of the Galois representations associated to ![]() $M_1$ and
$M_1$ and ![]() $M_2$ only if the ‘weights’ of all three Fontaine–Laffaille modules are in an interval of length
$M_2$ only if the ‘weights’ of all three Fontaine–Laffaille modules are in an interval of length ![]() $p-2$. See [Reference BooherBoo19, Fact 4.12], and for more details see the appendix of the arXiv version of [Reference BooherBoo19]. This causes substantial technical problems relating
$p-2$. See [Reference BooherBoo19, Fact 4.12], and for more details see the appendix of the arXiv version of [Reference BooherBoo19]. This causes substantial technical problems relating ![]() $G$-valued Galois representations to Fontaine–Laffaille modules with
$G$-valued Galois representations to Fontaine–Laffaille modules with ![]() $G$-structure, which we do not know how to resolve. This limitation explains why in [Reference PatrikisPat06, Reference BooherBoo19] the Hodge–Tate weights must lie in an interval of length less than
$G$-structure, which we do not know how to resolve. This limitation explains why in [Reference PatrikisPat06, Reference BooherBoo19] the Hodge–Tate weights must lie in an interval of length less than ![]() $(p-1)/2$ instead of
$(p-1)/2$ instead of ![]() $p-1$: one tensor product is needed to study the duality pairing.
$p-1$: one tensor product is needed to study the duality pairing.
1.2 Overview of the proof
We prove Theorem A by relating ![]() $G$-valued Galois representations to
$G$-valued Galois representations to ![]() $G$-Kisin modules. Many of the techniques are inspired by [Reference LevinLev15], which dealt with the very special case when the
$G$-Kisin modules. Many of the techniques are inspired by [Reference LevinLev15], which dealt with the very special case when the ![]() $p$-adic Hodge type is minuscule, and by [Reference Le, Le Hung, Levin and MorraLLHLM18, Reference Le, Le Hung, Levin and MorraLLHLM23] which introduce a
$p$-adic Hodge type is minuscule, and by [Reference Le, Le Hung, Levin and MorraLLHLM18, Reference Le, Le Hung, Levin and MorraLLHLM23] which introduce a ![]() $p$-adic approximation to the monodromy condition in
$p$-adic approximation to the monodromy condition in ![]() $p$-adic Hodge theory and connect this approximation to the geometry of affine Schubert varieties in the case of tamely potentially crystalline representation of small weight.
$p$-adic Hodge theory and connect this approximation to the geometry of affine Schubert varieties in the case of tamely potentially crystalline representation of small weight.
In § 2, we review some basics about ![]() $G$-bundles, affine Grassmanians, the Tannakian formalism for dealing with
$G$-bundles, affine Grassmanians, the Tannakian formalism for dealing with ![]() $G$-valued representations, and
$G$-valued representations, and ![]() $p$-adic Hodge theory for
$p$-adic Hodge theory for ![]() $G$-valued representations, in preparation for introducing
$G$-valued representations, in preparation for introducing ![]() $G$-Kisin modules in § 3. We define a variety of deformation problems for
$G$-Kisin modules in § 3. We define a variety of deformation problems for ![]() $G$-Kisin modules and
$G$-Kisin modules and ![]() $G$-valued Galois representations in § 3.3, and make precise the notion of ‘potential
$G$-valued Galois representations in § 3.3, and make precise the notion of ‘potential ![]() $p$-adic Hodge type for
$p$-adic Hodge type for ![]() ${\overline {\rho }}$’ that appears in Theorem A. The Kisin resolution
${\overline {\rho }}$’ that appears in Theorem A. The Kisin resolution ![]() $X_{{\overline {\rho }}}^{\mu } \rightarrow \operatorname {Spec} R^{\mu, \square }_{{\overline {\rho }}}$ is our main tool for relating Galois representations and Kisin modules. We ultimately show the resolution is an isomorphism and that
$X_{{\overline {\rho }}}^{\mu } \rightarrow \operatorname {Spec} R^{\mu, \square }_{{\overline {\rho }}}$ is our main tool for relating Galois representations and Kisin modules. We ultimately show the resolution is an isomorphism and that ![]() $X^{\mu }_{{\overline {\rho }}}$ is formally smooth.
$X^{\mu }_{{\overline {\rho }}}$ is formally smooth.
The analysis of the Kisin resolution occurs in §§ 6.1 and 6.2, and uses that ![]() $p$ is unramified in
$p$ is unramified in ![]() $K$ and that
$K$ and that ![]() $\mu$ is strongly Fontaine–Laffaille or that
$\mu$ is strongly Fontaine–Laffaille or that ![]() $G^{\operatorname {der}}$ is simply connected and
$G^{\operatorname {der}}$ is simply connected and ![]() $\mu$ is Fontaine–Laffaille. (This is the only step of the argument where
$\mu$ is Fontaine–Laffaille. (This is the only step of the argument where ![]() $\mu$ being Fontaine–Laffaille does not suffice.) An argument using the Bruhat order on affine Schubert varieties shows the Kisin variety is trivial, and hence
$\mu$ being Fontaine–Laffaille does not suffice.) An argument using the Bruhat order on affine Schubert varieties shows the Kisin variety is trivial, and hence ![]() $X_{{\overline {\rho }}}^{\mu }$ is local. We then make a delicate tangent space argument to show the Kisin resolution is an isomorphism.
$X_{{\overline {\rho }}}^{\mu }$ is local. We then make a delicate tangent space argument to show the Kisin resolution is an isomorphism.
Next, we embed ![]() $X_{{\overline {\rho }}}^{\mu }$ (up to formal variables) into rigidified deformations of
$X_{{\overline {\rho }}}^{\mu }$ (up to formal variables) into rigidified deformations of ![]() $G$-Kisin modules of type
$G$-Kisin modules of type ![]() $\leqslant \mu$, which in this introduction we denote by
$\leqslant \mu$, which in this introduction we denote by ![]() $\widetilde {D}_{\overline {\mathfrak {P}}}^{\leqslant \mu }$. We show it is an embedding in § 6.3 using the theory of
$\widetilde {D}_{\overline {\mathfrak {P}}}^{\leqslant \mu }$. We show it is an embedding in § 6.3 using the theory of ![]() $(\varphi,\widehat {\Gamma })$-modules with
$(\varphi,\widehat {\Gamma })$-modules with ![]() $G$-structure developed in [Reference LevinLev15]. We have to show that
$G$-structure developed in [Reference LevinLev15]. We have to show that ![]() $G$-Kisin modules of type
$G$-Kisin modules of type ![]() $\leqslant \mu$ admit at most one crystalline
$\leqslant \mu$ admit at most one crystalline ![]() $\widehat {\Gamma }$-structure; this requires that
$\widehat {\Gamma }$-structure; this requires that ![]() $\mu$ is Fontaine–Laffaille and
$\mu$ is Fontaine–Laffaille and ![]() $p$ is unramified in
$p$ is unramified in ![]() $K$.
$K$.
Given that the generic fiber of ![]() $X_{{\overline {\rho }}}^{\mu }$ consists of crystalline representation, it factors through the flat locus
$X_{{\overline {\rho }}}^{\mu }$ consists of crystalline representation, it factors through the flat locus ![]() $\widetilde {D}_{\overline {\mathfrak {P}}}^{\leqslant \mu, \nabla _{\infty }} \subset \widetilde {D}_{\overline {\mathfrak {P}}}^{\leqslant \mu }$ which satisfies the monodromy condition characterizing
$\widetilde {D}_{\overline {\mathfrak {P}}}^{\leqslant \mu, \nabla _{\infty }} \subset \widetilde {D}_{\overline {\mathfrak {P}}}^{\leqslant \mu }$ which satisfies the monodromy condition characterizing ![]() $G$-Kisin modules corresponding to crystalline representations. Let
$G$-Kisin modules corresponding to crystalline representations. Let ![]() $R^{\nabla _{\infty }}$ (respectively,
$R^{\nabla _{\infty }}$ (respectively, ![]() $R$) represent
$R$) represent ![]() $\widetilde {D}_{\overline {\mathfrak {P}}}^{\leqslant \mu, \nabla _{\infty }}$ (respectively,
$\widetilde {D}_{\overline {\mathfrak {P}}}^{\leqslant \mu, \nabla _{\infty }}$ (respectively, ![]() $\widetilde {D}_{\overline {\mathfrak {P}}}^{\leqslant \mu }$). We let
$\widetilde {D}_{\overline {\mathfrak {P}}}^{\leqslant \mu }$). We let ![]() $C \in G((W(k) \otimes R/pR)[\![u]\!] [1/u])$ represent the Frobenius on the universal
$C \in G((W(k) \otimes R/pR)[\![u]\!] [1/u])$ represent the Frobenius on the universal ![]() $G$-Kisin module over
$G$-Kisin module over ![]() $R/p R$. Via Tannakian formalism, we define an element
$R/p R$. Via Tannakian formalism, we define an element ![]() $u ({dC}/{du}) C^{-1}$ in
$u ({dC}/{du}) C^{-1}$ in ![]() $\operatorname {Lie} G \otimes (k \otimes R/pR)(\!(u)\!)$. The condition that
$\operatorname {Lie} G \otimes (k \otimes R/pR)(\!(u)\!)$. The condition that
i.e. that ![]() $u ({dC}/{du}) C^{-1}$ has no poles, is a closed condition on
$u ({dC}/{du}) C^{-1}$ has no poles, is a closed condition on ![]() $R/pR$ which we refer to as the mod
$R/pR$ which we refer to as the mod ![]() $p$ monodromy condition and denote by
$p$ monodromy condition and denote by ![]() $(R/pR)^{\nabla _1}$. By
$(R/pR)^{\nabla _1}$. By ![]() $p$-adically approximating the true monodromy condition, we prove the following theorem.
$p$-adically approximating the true monodromy condition, we prove the following theorem.
Theorem 1.2.1 (Theorem 4.2.6)
The special fiber of ![]() $\widetilde {D}_{\overline {\mathfrak {P}}}^{\leqslant \mu, \nabla _\infty }$ is contained in the locus of the special fiber of
$\widetilde {D}_{\overline {\mathfrak {P}}}^{\leqslant \mu, \nabla _\infty }$ is contained in the locus of the special fiber of ![]() $\widetilde {D}_{\overline {\mathfrak {P}}}^{\leqslant \mu }$ where the mod-
$\widetilde {D}_{\overline {\mathfrak {P}}}^{\leqslant \mu }$ where the mod-![]() $p$ monodromy condition holds; equivalently,
$p$ monodromy condition holds; equivalently,
The singularities of ![]() $\widetilde {D}_{\overline {\mathfrak {P}}}^{\leqslant \mu }$ are related to the singularities of a (mixed characteristic) affine Schubert variety
$\widetilde {D}_{\overline {\mathfrak {P}}}^{\leqslant \mu }$ are related to the singularities of a (mixed characteristic) affine Schubert variety ![]() $\prod _{\sigma \in \mathcal {J}} \operatorname {Gr}^{\leqslant \mu _{\sigma }}_G$, and the mod-
$\prod _{\sigma \in \mathcal {J}} \operatorname {Gr}^{\leqslant \mu _{\sigma }}_G$, and the mod-![]() $p$ monodromy condition can be descended to a condition on
$p$ monodromy condition can be descended to a condition on ![]() $\prod _{\sigma \in \mathcal {J}} \operatorname {Gr}^{\leqslant \mu _{\sigma }}_{G_{\mathbf {F}}}$, an affine Schubert variety. The ultimate source of smoothness then is that the differential equation (1.2.1) cuts out a smooth subvariety of the affine Schubert variety (Theorem 5.2.1).
$\prod _{\sigma \in \mathcal {J}} \operatorname {Gr}^{\leqslant \mu _{\sigma }}_{G_{\mathbf {F}}}$, an affine Schubert variety. The ultimate source of smoothness then is that the differential equation (1.2.1) cuts out a smooth subvariety of the affine Schubert variety (Theorem 5.2.1).
To complete the proof of Theorem A, we collect the relationships between all the deformation problems in Theorem 6.4.2 and compare dimensions. Theorem 6.4.4 provides a more technical version of Theorem A. It also offers some information for free about the non-existence of crystalline lifts with particular ![]() $p$-adic Hodge types (Corollary 6.4.6).
$p$-adic Hodge types (Corollary 6.4.6).
1.3 Notation
We collect some standard notation that will repeatedly arise for easy reference.
Fix a prime ![]() $p$. Our standard convention is for
$p$. Our standard convention is for ![]() $\Lambda$ to be the ring of integers in a
$\Lambda$ to be the ring of integers in a ![]() $p$-adic field
$p$-adic field ![]() $L$ with residue field
$L$ with residue field ![]() $\mathbf {F}$, and for
$\mathbf {F}$, and for ![]() $G$ to be a split reductive group over
$G$ to be a split reductive group over ![]() $\Lambda$. We denote the derived group (respectively, adjoint group) of
$\Lambda$. We denote the derived group (respectively, adjoint group) of ![]() $G$ by
$G$ by ![]() $G^{\operatorname {der}}$ (respectively,
$G^{\operatorname {der}}$ (respectively, ![]() $G^{\mathrm {ad}}$) and often use
$G^{\mathrm {ad}}$) and often use ![]() $Z$ and
$Z$ and ![]() $Z^{\operatorname {der}}$ to denote the centers of
$Z^{\operatorname {der}}$ to denote the centers of ![]() $G$ and
$G$ and ![]() $G^{\operatorname {der}}$. In many places, we assume that
$G^{\operatorname {der}}$. In many places, we assume that ![]() $p \nmid \pi _1(G^{\operatorname {der}})$.
$p \nmid \pi _1(G^{\operatorname {der}})$.
We often fix a finite field ![]() $k$ and a
$k$ and a ![]() $p$-adic field
$p$-adic field ![]() $K$ with ring of integers
$K$ with ring of integers ![]() $W(k)$. We let
$W(k)$. We let ![]() $G' := \operatorname {Res}_{(W(k) \otimes \Lambda )/ \Lambda } G$. When
$G' := \operatorname {Res}_{(W(k) \otimes \Lambda )/ \Lambda } G$. When ![]() $\Lambda$ contains a copy of
$\Lambda$ contains a copy of ![]() $W(k)$, we have that
$W(k)$, we have that ![]() $G' = \prod _{\sigma \in \operatorname {Hom}(K, L)} G$.
$G' = \prod _{\sigma \in \operatorname {Hom}(K, L)} G$.
1.3.1 Root systems
We fix a split maximal torus ![]() $T \subset G$ and a Borel subgroup
$T \subset G$ and a Borel subgroup ![]() $B$ of
$B$ of ![]() $G$ containing
$G$ containing ![]() $T$. Let
$T$. Let ![]() $X^*(T)$ and
$X^*(T)$ and ![]() $X_*(T)$ denote the character and cocharacter lattices of
$X_*(T)$ denote the character and cocharacter lattices of ![]() $T$. We let
$T$. We let ![]() $\Phi _G \subset X^*(T)$ and
$\Phi _G \subset X^*(T)$ and ![]() $\Phi _G^\vee \subset X_*(T)$ denote the roots and coroots for
$\Phi _G^\vee \subset X_*(T)$ denote the roots and coroots for ![]() $(G,T)$. We let
$(G,T)$. We let ![]() $\langle \mu, \chi \rangle$ denote the standard pairing between a cocharacter
$\langle \mu, \chi \rangle$ denote the standard pairing between a cocharacter ![]() $\mu$ and a character
$\mu$ and a character ![]() $\lambda$.
$\lambda$.
Let ![]() $\Phi _G^+$ denote the set of positive roots with respect to
$\Phi _G^+$ denote the set of positive roots with respect to ![]() $B$, and
$B$, and ![]() $X_*(T)_+$ the set of dominant cocharacters. For a cocharacter
$X_*(T)_+$ the set of dominant cocharacters. For a cocharacter ![]() $\mu$, let
$\mu$, let ![]() $\mu ^{\operatorname {dom}}$ be the unique dominant cocharacter in the same Weyl orbit as
$\mu ^{\operatorname {dom}}$ be the unique dominant cocharacter in the same Weyl orbit as ![]() $\mu$. There is a partial ordering on
$\mu$. There is a partial ordering on ![]() $X_*(T)_+$ where
$X_*(T)_+$ where ![]() $\lambda \leqslant \mu$ if
$\lambda \leqslant \mu$ if ![]() $\mu - \lambda$ is a non-negative combination of simple coroots.
$\mu - \lambda$ is a non-negative combination of simple coroots.
For a cocharacter ![]() $\mu$ of
$\mu$ of ![]() $G$, we define
$G$, we define
1.3.2 Lie algebras
We let ![]() $\mathfrak {g}$ denote the Lie algebra of
$\mathfrak {g}$ denote the Lie algebra of ![]() $G$,
$G$, ![]() $\mathfrak {t}$ the Lie algebra of a split maximal torus
$\mathfrak {t}$ the Lie algebra of a split maximal torus ![]() $T$, and denote the root space for
$T$, and denote the root space for ![]() $\alpha \in \Phi _G$ by
$\alpha \in \Phi _G$ by ![]() $\mathfrak {g}_\alpha$. For a
$\mathfrak {g}_\alpha$. For a ![]() $\Lambda$-algebra
$\Lambda$-algebra ![]() $A$, we let
$A$, we let ![]() $\mathfrak {g}_A$ denote
$\mathfrak {g}_A$ denote ![]() $\mathfrak {g} \otimes _{\Lambda } A$, or equivalently the Lie algebra of
$\mathfrak {g} \otimes _{\Lambda } A$, or equivalently the Lie algebra of ![]() $G_A$. We use
$G_A$. We use ![]() $\mathfrak {g}'$ (respectively,
$\mathfrak {g}'$ (respectively, ![]() $\mathfrak {t}'$,…) for the Lie algebra of the Weil restriction
$\mathfrak {t}'$,…) for the Lie algebra of the Weil restriction ![]() $G'$ (respectively, the Lie algebra of a split maximal torus
$G'$ (respectively, the Lie algebra of a split maximal torus ![]() $T'$,…).
$T'$,…).
1.3.3 Affine Grassmanians
Almost all of our work with affine Grassmanians will involve the group ![]() $G'$. We use
$G'$. We use ![]() $\operatorname {LG}'$,
$\operatorname {LG}'$, ![]() $\textrm {L}^+G'$, and
$\textrm {L}^+G'$, and ![]() $\operatorname {Gr}_{G'}$ to denote the loop group, positive loop groups, and affine Grassmanian for
$\operatorname {Gr}_{G'}$ to denote the loop group, positive loop groups, and affine Grassmanian for ![]() $G'$ over
$G'$ over ![]() $\Lambda$. When
$\Lambda$. When ![]() $p \nmid \pi _1(G^{\operatorname {der}})$ (or, equivalently,
$p \nmid \pi _1(G^{\operatorname {der}})$ (or, equivalently, ![]() $p \nmid \pi _1((G')^{\operatorname {der}})$), we also use
$p \nmid \pi _1((G')^{\operatorname {der}})$), we also use ![]() $\operatorname {Gr}_{G'}^{\leqslant \mu }$ over
$\operatorname {Gr}_{G'}^{\leqslant \mu }$ over ![]() $\Lambda$; see § 2.3.
$\Lambda$; see § 2.3.
Over the residue field ![]() $\mathbf {F}$, we let
$\mathbf {F}$, we let ![]() $\operatorname {Gr}^{\leqslant \mu }_{G'_{\mathbf {F}}}$ and
$\operatorname {Gr}^{\leqslant \mu }_{G'_{\mathbf {F}}}$ and ![]() $\operatorname {Gr}^{\circ, \mu }_{G'_{\mathbf {F}}}$ denote the Schubert variety and open Schubert cell for a cocharacter
$\operatorname {Gr}^{\circ, \mu }_{G'_{\mathbf {F}}}$ denote the Schubert variety and open Schubert cell for a cocharacter ![]() $\mu$ of
$\mu$ of ![]() $G'$.
$G'$.
1.3.4 Galois representations
Let ![]() $K$ be a
$K$ be a ![]() $p$-adic field unramified over
$p$-adic field unramified over ![]() $\mathbf {Q}_p$ with fixed algebraic closure
$\mathbf {Q}_p$ with fixed algebraic closure ![]() $\overline {K}$. Let
$\overline {K}$. Let ![]() $k$ be its residue field and
$k$ be its residue field and ![]() $W(k)$ the ring of integers in
$W(k)$ the ring of integers in ![]() $K$. Let
$K$. Let ![]() $\Gamma _K = \operatorname {Gal}(\overline {K}/ K)$ be its absolute Galois group. We usually fix a continuous homomorphism
$\Gamma _K = \operatorname {Gal}(\overline {K}/ K)$ be its absolute Galois group. We usually fix a continuous homomorphism ![]() ${\overline {\rho }} : \Gamma _K \to G(\mathbf {F})$.
${\overline {\rho }} : \Gamma _K \to G(\mathbf {F})$.
Fix a compatible system ![]() $\{p^{1/p}, p^{1/p^2}, \ldots \}$ of
$\{p^{1/p}, p^{1/p^2}, \ldots \}$ of ![]() $p$-power roots of
$p$-power roots of ![]() $p$, and let
$p$, and let ![]() $K_\infty = K(p^{1/p},p^{1/p^2},\ldots )$. We let
$K_\infty = K(p^{1/p},p^{1/p^2},\ldots )$. We let ![]() $\Gamma _\infty$ be the absolute Galois group of
$\Gamma _\infty$ be the absolute Galois group of ![]() $K_\infty$ (with respect to
$K_\infty$ (with respect to ![]() $\overline {K}$).
$\overline {K}$).
1.3.5 Big rings
Let ![]() $\mathfrak {S} := W(k)[\![u ] \!]$ and
$\mathfrak {S} := W(k)[\![u ] \!]$ and ![]() $E(u) = u -p$. We set
$E(u) = u -p$. We set ![]() $\mathcal {O}_{\mathcal {E}}$ to be the
$\mathcal {O}_{\mathcal {E}}$ to be the ![]() $p$-adic completion of
$p$-adic completion of ![]() $\mathfrak {S}[ {1}/{u}]$. The rings
$\mathfrak {S}[ {1}/{u}]$. The rings ![]() $\mathfrak {S}$ and
$\mathfrak {S}$ and ![]() $\mathcal {O}_{\mathcal {E}}$ are equipped with a Frobenius
$\mathcal {O}_{\mathcal {E}}$ are equipped with a Frobenius ![]() $\varphi$ by extending the standard Frobenius on
$\varphi$ by extending the standard Frobenius on ![]() $W(k)$ by sending
$W(k)$ by sending ![]() $u$ to
$u$ to ![]() $u^p$.
$u^p$.
For any ![]() $p$-adically complete
$p$-adically complete ![]() $\mathbf {Z}_p$-algebra
$\mathbf {Z}_p$-algebra ![]() $A$, we set
$A$, we set ![]() $\mathfrak {S}_A := (W(k) \otimes _{\mathbf {Z}_p} A)[\![u]\!]$ and
$\mathfrak {S}_A := (W(k) \otimes _{\mathbf {Z}_p} A)[\![u]\!]$ and ![]() $\mathcal {O}_{\mathcal {E},A}$ is the
$\mathcal {O}_{\mathcal {E},A}$ is the ![]() $p$-adic completion of
$p$-adic completion of ![]() $\mathfrak {S}_A[1/u]$. We extend Frobenius to both by having it act trivially on
$\mathfrak {S}_A[1/u]$. We extend Frobenius to both by having it act trivially on ![]() $A$. Note that if
$A$. Note that if ![]() $A$ is finite over
$A$ is finite over ![]() $\mathbf {Z}_p$ (for example, Artinian), then
$\mathbf {Z}_p$ (for example, Artinian), then ![]() $\mathfrak {S}_A = \mathfrak {S} \otimes _{\mathbf {Z}_p} A$.
$\mathfrak {S}_A = \mathfrak {S} \otimes _{\mathbf {Z}_p} A$.
1.3.6 Kisin modules
A type for ![]() $G$ is a cocharacter
$G$ is a cocharacter ![]() $\mu$ for the group
$\mu$ for the group ![]() $G'$. We usually use
$G'$. We usually use ![]() $\mathfrak {P}$ to denote a
$\mathfrak {P}$ to denote a ![]() $G$-Kisin module (Definition 3.1.1), and denote the category of
$G$-Kisin module (Definition 3.1.1), and denote the category of ![]() $G$-Kisin modules of type
$G$-Kisin modules of type ![]() $\leqslant \mu$ with coefficients in a
$\leqslant \mu$ with coefficients in a ![]() $\Lambda$-algebra
$\Lambda$-algebra ![]() $A$ by
$A$ by ![]() $Y^{\leqslant \mu }(A)$ (Definition 3.1.7).
$Y^{\leqslant \mu }(A)$ (Definition 3.1.7).
1.3.7 Deformation functors
Let ![]() $\mathcal {C}_{\Lambda }$ (respectively,
$\mathcal {C}_{\Lambda }$ (respectively, ![]() $\widehat {\mathcal {C}}_{\Lambda }$) denote the categories of coefficient
$\widehat {\mathcal {C}}_{\Lambda }$) denote the categories of coefficient ![]() $\Lambda$-algebras: local Artinian
$\Lambda$-algebras: local Artinian ![]() $\Lambda$-algebras with residue field
$\Lambda$-algebras with residue field ![]() $\mathbf {F}$ (respectively, complete local Noetherian
$\mathbf {F}$ (respectively, complete local Noetherian ![]() $\Lambda$-algebras with residue field
$\Lambda$-algebras with residue field ![]() $\mathbf {F}$). Morphisms are local
$\mathbf {F}$). Morphisms are local ![]() $\Lambda$-algebra maps.
$\Lambda$-algebra maps.
Our deformation problems are functors from ![]() $\mathcal {C}_{\Lambda }$ (or
$\mathcal {C}_{\Lambda }$ (or ![]() $\widehat {\mathcal {C}}_{\Lambda }$) to sets. A variety of deformation problems (
$\widehat {\mathcal {C}}_{\Lambda }$) to sets. A variety of deformation problems (![]() $D_{{\overline {\rho }}}^{\mu,\square }$,
$D_{{\overline {\rho }}}^{\mu,\square }$, ![]() $D_{{\overline {\rho }}, \overline {\mathfrak {P}}}^{\mu,\square }$, etc.) and their associated deformation rings (
$D_{{\overline {\rho }}, \overline {\mathfrak {P}}}^{\mu,\square }$, etc.) and their associated deformation rings (![]() $R_{{\overline {\rho }}}^{\mu,\square }$,
$R_{{\overline {\rho }}}^{\mu,\square }$, ![]() $R_{{\overline {\rho }}, \overline {\mathfrak {P}}}^{\mu,\square }$, etc.) can be found in Fact 2.4.2 and Definitions 3.3.1, 3.3.2, 3.3.5, and 6.4.1. Theorem 6.4.2 shows the relationships between many of them.
$R_{{\overline {\rho }}, \overline {\mathfrak {P}}}^{\mu,\square }$, etc.) can be found in Fact 2.4.2 and Definitions 3.3.1, 3.3.2, 3.3.5, and 6.4.1. Theorem 6.4.2 shows the relationships between many of them.
2. Preliminaries
Let ![]() $G$ be a split reductive group defined the ring of integers
$G$ be a split reductive group defined the ring of integers ![]() $\Lambda$ in a
$\Lambda$ in a ![]() $p$-adic field
$p$-adic field ![]() $L$ with residue field
$L$ with residue field ![]() $\mathbf {F}$. We begin by reviewing some background about
$\mathbf {F}$. We begin by reviewing some background about ![]() $G$-bundles, the Tannakian formalism, affine Grassmanians, and
$G$-bundles, the Tannakian formalism, affine Grassmanians, and ![]() $p$-adic Hodge theory for
$p$-adic Hodge theory for ![]() $G$-valued representations.
$G$-valued representations.
2.1  $G$-bundles
$G$-bundles
In what follows, all ![]() $G$-bundles are with respect to the fppf topology. We begin by recalling a few things about
$G$-bundles are with respect to the fppf topology. We begin by recalling a few things about ![]() $G$-valued representations and trivializations of
$G$-valued representations and trivializations of ![]() $G$-bundles.
$G$-bundles.
Definition 2.1.1 For any profinite group ![]() $\Gamma$ and a finite
$\Gamma$ and a finite ![]() $\Lambda$-algebra
$\Lambda$-algebra ![]() $A$, let
$A$, let ![]() $\operatorname {GRep}_A(\Gamma )$ be the category of pairs
$\operatorname {GRep}_A(\Gamma )$ be the category of pairs ![]() $(P,\rho )$ where
$(P,\rho )$ where ![]() $P$ is a
$P$ is a ![]() $G$-bundle on
$G$-bundle on ![]() $\operatorname {Spec} A$ and
$\operatorname {Spec} A$ and ![]() $\rho : \Gamma \to \operatorname {Aut}_G(P)$ is a continuous homomorphism (giving
$\rho : \Gamma \to \operatorname {Aut}_G(P)$ is a continuous homomorphism (giving ![]() $A$ the
$A$ the ![]() $p$-adic topology).
$p$-adic topology).
Definition 2.1.2 A trivialization of a ![]() $G$-bundle
$G$-bundle ![]() $\mathfrak {P}$ on
$\mathfrak {P}$ on ![]() $X$ is an isomorphism with the trivial
$X$ is an isomorphism with the trivial ![]() $G$-bundle
$G$-bundle ![]() $\mathcal {E}^0_X$ on
$\mathcal {E}^0_X$ on ![]() $X$.
$X$.
We know that if ![]() $A$ is a complete local
$A$ is a complete local ![]() $\Lambda$-algebra with finite residue field, then any
$\Lambda$-algebra with finite residue field, then any ![]() $G$-bundle on
$G$-bundle on ![]() $A$ is trivializable [Reference LevinLev15, Proposition 2.1.4]. Thus, in all cases we consider,
$A$ is trivializable [Reference LevinLev15, Proposition 2.1.4]. Thus, in all cases we consider, ![]() $\operatorname {Aut}_G(P)$ is (non-canonically) isomorphic to
$\operatorname {Aut}_G(P)$ is (non-canonically) isomorphic to ![]() $G(A)$. Identifying
$G(A)$. Identifying ![]() $\operatorname {Aut}_G(P)$ with
$\operatorname {Aut}_G(P)$ with ![]() $G(A)$ is equivalent to choosing a trivialization. A continuous homomorphism
$G(A)$ is equivalent to choosing a trivialization. A continuous homomorphism ![]() $\rho : \Gamma \to G(A)$ is equivalent to
$\rho : \Gamma \to G(A)$ is equivalent to ![]() $(P,\rho ') \in \operatorname {GRep}_A(\Gamma )$ together with a trivialization of
$(P,\rho ') \in \operatorname {GRep}_A(\Gamma )$ together with a trivialization of ![]() $P$.
$P$.
Remark 2.1.3 For ![]() $G = \operatorname {GL}_n$,
$G = \operatorname {GL}_n$, ![]() $G$-bundles are vector bundles in the Zariski topology. If
$G$-bundles are vector bundles in the Zariski topology. If ![]() $A$ is a complete local
$A$ is a complete local ![]() $\Lambda$-algebra with finite residue field then the vector bundle is given by a finitely generated projective (hence, free) module over
$\Lambda$-algebra with finite residue field then the vector bundle is given by a finitely generated projective (hence, free) module over ![]() $A$ and a trivialization is a choice of basis.
$A$ and a trivialization is a choice of basis.
2.2 Tannakian formalism
Now let ![]() ${^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$ denote the category of representations of the algebraic group
${^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$ denote the category of representations of the algebraic group ![]() $G$ on finite free
$G$ on finite free ![]() $\Lambda$-modules, and
$\Lambda$-modules, and ![]() $\operatorname {Proj}_A$ denote the category of projective
$\operatorname {Proj}_A$ denote the category of projective ![]() $A$-modules. For a
$A$-modules. For a ![]() $\Lambda$-algebra
$\Lambda$-algebra ![]() $A$, a
$A$, a ![]() $G$-bundle
$G$-bundle ![]() $\mathfrak {P}$ on
$\mathfrak {P}$ on ![]() $\operatorname {Spec} (A)$ is equivalent to a fiber functor
$\operatorname {Spec} (A)$ is equivalent to a fiber functor ![]() $\eta : {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G) \to \operatorname {Proj}_A$ (a faithful exact tensor functor sending the trivial representation to the trivial
$\eta : {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G) \to \operatorname {Proj}_A$ (a faithful exact tensor functor sending the trivial representation to the trivial ![]() $A$-module of rank
$A$-module of rank ![]() $1$); the fiber functor associated to
$1$); the fiber functor associated to ![]() $\mathfrak {P}$ sends a representation
$\mathfrak {P}$ sends a representation ![]() $G \to GL(V)$ to the pushout
$G \to GL(V)$ to the pushout ![]() $\mathfrak {P}_V$ (see [Reference LevinLev15, Theorem 2.1.1] for this level of generality). This allows us to give ‘additional structure’ on the
$\mathfrak {P}_V$ (see [Reference LevinLev15, Theorem 2.1.1] for this level of generality). This allows us to give ‘additional structure’ on the ![]() $G$-bundle
$G$-bundle ![]() $\mathfrak {P}$ by factoring
$\mathfrak {P}$ by factoring ![]() $\eta$ through a category of projective
$\eta$ through a category of projective ![]() $A$-modules with ‘additional structure’; equivalently, by specifying ‘additional structure’ on the
$A$-modules with ‘additional structure’; equivalently, by specifying ‘additional structure’ on the ![]() $\Lambda$-modules
$\Lambda$-modules ![]() $\eta (V)$ for each
$\eta (V)$ for each ![]() $G \to \operatorname {GL}(V)$ that are compatible in an appropriate sense.
$G \to \operatorname {GL}(V)$ that are compatible in an appropriate sense.
Example 2.2.1 We make this idea precise in a few important examples.
(a) An automorphism of the fiber functor
 $\eta$ corresponds to an automorphism of the
$\eta$ corresponds to an automorphism of the  $G$-bundle (see [Reference LevinLev13, Theorem 2.5.2] for this level of generality). In our situations, the
$G$-bundle (see [Reference LevinLev13, Theorem 2.5.2] for this level of generality). In our situations, the  $G$-bundle can be trivialized, so
$G$-bundle can be trivialized, so  $\eta (V) \simeq V_A$ and a choice of trivialization identifies
$\eta (V) \simeq V_A$ and a choice of trivialization identifies  $\operatorname {Aut}(\eta ) \simeq \operatorname {Aut}_G(\mathfrak {P}) \simeq G$. In particular, we see that
$\operatorname {Aut}(\eta ) \simeq \operatorname {Aut}_G(\mathfrak {P}) \simeq G$. In particular, we see that  $G(A)$ is in bijection with collections of elements
$G(A)$ is in bijection with collections of elements  $g_V \in \operatorname {GL}(V_A)$ for
$g_V \in \operatorname {GL}(V_A)$ for  $V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$ that are compatible with tensor products and exact sequences in the sense that
$V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$ that are compatible with tensor products and exact sequences in the sense that  $g_{V_1 \otimes V_2 } = g_{V_1} \otimes g_{V_2}$ and such that for short exact sequences
$g_{V_1 \otimes V_2 } = g_{V_1} \otimes g_{V_2}$ and such that for short exact sequences  $0 \to V_1 \to V \to V_2 \to 0$ in
$0 \to V_1 \to V \to V_2 \to 0$ in  ${^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$ the following diagram commutes.
Furthermore,
${^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$ the following diagram commutes.
Furthermore,
 $g_{\mathbf {1}} = \operatorname {id}$.
$g_{\mathbf {1}} = \operatorname {id}$.(b) We can extend the previous example to treat a representation of a group
 $\Gamma$ valued in
$\Gamma$ valued in  $G(A)$ as a compatible set of representations of
$G(A)$ as a compatible set of representations of  $\Gamma$ on
$\Gamma$ on  $V_A$ for
$V_A$ for  $V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$.
$V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$.(c) Similarly, an element
 $X \in \mathfrak {g}_A$ is equivalent to endomorphisms
$X \in \mathfrak {g}_A$ is equivalent to endomorphisms  $X_V$ in
$X_V$ in  $\operatorname {End}(V_A)$ for
$\operatorname {End}(V_A)$ for  $V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$ (with
$V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$ (with  $X_{\mathbf {1}} =0$) that are compatible with exact sequences and with tensor products in the sense that
$X_{\mathbf {1}} =0$) that are compatible with exact sequences and with tensor products in the sense that  $X_{V \otimes V'} = X_{V} \otimes 1 + 1 \otimes X_{V'}$. This follows from the dual-number interpretation of the Lie algebra and example (a).
$X_{V \otimes V'} = X_{V} \otimes 1 + 1 \otimes X_{V'}$. This follows from the dual-number interpretation of the Lie algebra and example (a).(d) A
 $G$-grading is a fiber functor which factors through the category of graded vector bundles on
$G$-grading is a fiber functor which factors through the category of graded vector bundles on  $\operatorname {Spec}(A)$. This corresponds to giving a grading on each
$\operatorname {Spec}(A)$. This corresponds to giving a grading on each  $\eta (V) \simeq V_A$ for each
$\eta (V) \simeq V_A$ for each  $V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$. The gradings are compatible with exact sequences, and with tensor products in the sense that (using subscripts to denote graded pieces)
Furthermore,
$V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$. The gradings are compatible with exact sequences, and with tensor products in the sense that (using subscripts to denote graded pieces)
Furthermore, \[ (V \otimes V')_n = \bigoplus_{ i+j=n} V_i \otimes V'_j. \]
\[ (V \otimes V')_n = \bigoplus_{ i+j=n} V_i \otimes V'_j. \]
 $(\mathbf {1})_0 = \mathbf {1}$. This can equivalently be described via a cocharacter
$(\mathbf {1})_0 = \mathbf {1}$. This can equivalently be described via a cocharacter  $\mu : \mathbf {G}_m \to \operatorname {Aut}_G(\mathfrak {P})$, arising by letting
$\mu : \mathbf {G}_m \to \operatorname {Aut}_G(\mathfrak {P})$, arising by letting  $t \in \mathbf {G}_m$ act on
$t \in \mathbf {G}_m$ act on  $V_n$ via multiplication by
$V_n$ via multiplication by  $t^n$.
$t^n$.(e) There is an analogous description of
 $G$-filtrations as fiber functors
$G$-filtrations as fiber functors  $\eta$ factoring through the category
$\eta$ factoring through the category  $\operatorname {Fil}_{A}$ of vector bundles on
$\operatorname {Fil}_{A}$ of vector bundles on  $\operatorname {Spec}(A)$ with decreasing filtration. A splitting is an isomorphism of a
$\operatorname {Spec}(A)$ with decreasing filtration. A splitting is an isomorphism of a  $G$-grading with the composition of
$G$-grading with the composition of  $\eta$ with the associated graded functor. In the setting we are working in, all
$\eta$ with the associated graded functor. In the setting we are working in, all  $G$-gradings are split [Reference RivanoRiv72, Proposition IV.2.2.5]. The type of the filtration is the geometric conjugacy class of cocharacters of
$G$-gradings are split [Reference RivanoRiv72, Proposition IV.2.2.5]. The type of the filtration is the geometric conjugacy class of cocharacters of  $G$ giving the splitting.
$G$ giving the splitting.
2.3 Affine Grassmannians
Let ![]() $G$ be a split reductive group over
$G$ be a split reductive group over ![]() $\Lambda$, and fix a split maximal torus
$\Lambda$, and fix a split maximal torus ![]() $T$ and set of positive roots. We make use of a mixed characteristic affine Grassmannian. In the context where they arise, the affine Grassmannians are centered at
$T$ and set of positive roots. We make use of a mixed characteristic affine Grassmannian. In the context where they arise, the affine Grassmannians are centered at ![]() $u = p$ and involve a Weil restriction. We focus on that setup.
$u = p$ and involve a Weil restriction. We focus on that setup.
We let ![]() $\operatorname {LG}$ and
$\operatorname {LG}$ and ![]() $\textrm {L}^+G$ denote the loop group and the positive loop group for
$\textrm {L}^+G$ denote the loop group and the positive loop group for ![]() $G$ over
$G$ over ![]() $\Lambda$. For a
$\Lambda$. For a ![]() $\Lambda$-algebra
$\Lambda$-algebra ![]() $A$, we have that
$A$, we have that
The affine Grassmanian ![]() $\operatorname {Gr}_{G}$ is the fpqc quotient
$\operatorname {Gr}_{G}$ is the fpqc quotient ![]() $\textrm {L}^+G \backslash \operatorname {LG}$. It is an ind-projective scheme. If
$\textrm {L}^+G \backslash \operatorname {LG}$. It is an ind-projective scheme. If ![]() $\rho :G \rightarrow H$ is any homomorphism of algebraic groups, then there is natural induced map
$\rho :G \rightarrow H$ is any homomorphism of algebraic groups, then there is natural induced map ![]() $\rho _*:\operatorname {Gr}_G \rightarrow \operatorname {Gr}_H$. Given
$\rho _*:\operatorname {Gr}_G \rightarrow \operatorname {Gr}_H$. Given ![]() $C \in \operatorname {LG}(A)$, we let
$C \in \operatorname {LG}(A)$, we let ![]() $[C]$ denote the equivalence class in the quotient
$[C]$ denote the equivalence class in the quotient ![]() $\operatorname {Gr}_G(A)$.
$\operatorname {Gr}_G(A)$.
The special fiber ![]() $\operatorname {Gr}_{G_{\mathbf {F}}}$ is just the usual affine Grassmannian for
$\operatorname {Gr}_{G_{\mathbf {F}}}$ is just the usual affine Grassmannian for ![]() $G$ centered at
$G$ centered at ![]() $u = 0$. For any cocharacter
$u = 0$. For any cocharacter ![]() $\mu$ of
$\mu$ of ![]() $T$, we use
$T$, we use ![]() $(u-p)^{\mu }$ to denote the element
$(u-p)^{\mu }$ to denote the element ![]() $\mu (u-p) \in L T(\Lambda ) \subset LG(\Lambda )$ and
$\mu (u-p) \in L T(\Lambda ) \subset LG(\Lambda )$ and ![]() $[(u-p)^{\mu }]$ denote the corresponding
$[(u-p)^{\mu }]$ denote the corresponding ![]() $\Lambda$-point of
$\Lambda$-point of ![]() $\operatorname {Gr}_{G}$. When working in special fiber, we use
$\operatorname {Gr}_{G}$. When working in special fiber, we use ![]() $u^{\mu }$ and
$u^{\mu }$ and ![]() $[u^{\mu }]$ with the obvious meaning.
$[u^{\mu }]$ with the obvious meaning.
Given dominant cocharacters ![]() $\mu '$ and
$\mu '$ and ![]() $\mu$ of
$\mu$ of ![]() $G$, recall that
$G$, recall that ![]() $\mu ' \leqslant \mu$ if
$\mu ' \leqslant \mu$ if ![]() $\mu -\mu '$ is a non-negative linear combination of simple coroots. Let
$\mu -\mu '$ is a non-negative linear combination of simple coroots. Let ![]() $\operatorname {Gr}^{\leqslant \mu }_{G_{\mathbf {F}}}$ and
$\operatorname {Gr}^{\leqslant \mu }_{G_{\mathbf {F}}}$ and ![]() $\operatorname {Gr}^{\circ, \mu }_{G_{\mathbf {F}}}$ denote the affine Schubert variety and open affine Schubert cell for the cocharacter
$\operatorname {Gr}^{\circ, \mu }_{G_{\mathbf {F}}}$ denote the affine Schubert variety and open affine Schubert cell for the cocharacter ![]() $\mu$, which are the orbit closure and orbit respectively of
$\mu$, which are the orbit closure and orbit respectively of ![]() $\textrm {L}^+G$ on
$\textrm {L}^+G$ on ![]() $u^{\mu }$. These only depend on the conjugacy class of
$u^{\mu }$. These only depend on the conjugacy class of ![]() $\mu$, so it is convenient to work with dominant representative.
$\mu$, so it is convenient to work with dominant representative.
Theorem 2.3.1 Assume that ![]() $p \nmid \# \pi _1(G^{\mathrm {der}})$ then there is a projective flat
$p \nmid \# \pi _1(G^{\mathrm {der}})$ then there is a projective flat ![]() $\Lambda$-scheme
$\Lambda$-scheme ![]() $\operatorname {Gr}_G^{\leqslant \mu }$ such that
$\operatorname {Gr}_G^{\leqslant \mu }$ such that
and the generic fiber ![]() $(\operatorname {Gr}_G^{\leqslant \mu })_{L}$ is the reduced closure of the
$(\operatorname {Gr}_G^{\leqslant \mu })_{L}$ is the reduced closure of the ![]() $\textrm {L}^+G_{L}$-orbit of
$\textrm {L}^+G_{L}$-orbit of ![]() $(u-p)^{\mu }$.
$(u-p)^{\mu }$.
Proof. When ![]() $G$ is simply connected, there is a construction of affine Schubert varieties over any base on p. 52 of [Reference FaltingsFal03]. Under the assumption on the fundamental group, one can reduce to this case. For lack of a better reference, the theorem is also a consequence of [Reference Pappas and ZhuPZ13, Theorem 9.3] since
$G$ is simply connected, there is a construction of affine Schubert varieties over any base on p. 52 of [Reference FaltingsFal03]. Under the assumption on the fundamental group, one can reduce to this case. For lack of a better reference, the theorem is also a consequence of [Reference Pappas and ZhuPZ13, Theorem 9.3] since ![]() $\operatorname {Gr}^{\leqslant \mu }_{G}$ is a very special case of the Pappas–Zhu local model associated to
$\operatorname {Gr}^{\leqslant \mu }_{G}$ is a very special case of the Pappas–Zhu local model associated to ![]() $G$, the conjugacy class of
$G$, the conjugacy class of ![]() $\mu$, and the maximal compact parahoric
$\mu$, and the maximal compact parahoric ![]() $G(\Lambda )$.
$G(\Lambda )$.
Remark 2.3.2 Let ![]() $\mu$ be dominant. The affine Schubert variety
$\mu$ be dominant. The affine Schubert variety ![]() $\operatorname {Gr}^{\leqslant \mu }_{G_\mathbf {F}}$ is the union of
$\operatorname {Gr}^{\leqslant \mu }_{G_\mathbf {F}}$ is the union of ![]() $\operatorname {Gr}^{\circ, \mu '}_{G_\mathbf {F}}$ for dominant
$\operatorname {Gr}^{\circ, \mu '}_{G_\mathbf {F}}$ for dominant ![]() $\mu ' \leqslant \mu$. This can also be phrased in terms of the Cartan decomposition. For
$\mu ' \leqslant \mu$. This can also be phrased in terms of the Cartan decomposition. For ![]() $C \in \operatorname {LG}(\mathbf {F})$, we have that
$C \in \operatorname {LG}(\mathbf {F})$, we have that ![]() $[C] \in \operatorname {Gr}^{\leqslant \mu }_{G_\mathbf {F}}$ if and only if there exists dominant
$[C] \in \operatorname {Gr}^{\leqslant \mu }_{G_\mathbf {F}}$ if and only if there exists dominant ![]() $\mu ' \leqslant \mu$ such that
$\mu ' \leqslant \mu$ such that
For later use, we now record a standard fact about tangent spaces. We use our standard notation about root systems and Lie algebras from §§ 1.3.1–1.3.2.
Lemma 2.3.3 The map on tangent spaces induced by right multiplication by ![]() $u^\mu$ on
$u^\mu$ on ![]() $\operatorname {Gr}_{G_\mathbf {F}}$ identifies
$\operatorname {Gr}_{G_\mathbf {F}}$ identifies
with the tangent space of ![]() $\operatorname {Gr}^{\circ, \mu }_{G_{\mathbf {F}}}$ at
$\operatorname {Gr}^{\circ, \mu }_{G_{\mathbf {F}}}$ at ![]() $[u^\mu ]$ as a subspace of the tangent space of
$[u^\mu ]$ as a subspace of the tangent space of ![]() $\operatorname {Gr}_{G_\mathbf {F}}$ at
$\operatorname {Gr}_{G_\mathbf {F}}$ at ![]() $[u^\mu ]$.
$[u^\mu ]$.
Proof. First, note that the stabilizer of ![]() $[u^{\mu }] \in \operatorname {Gr}_{G_\mathbf {F}}$ under right multiplication by
$[u^{\mu }] \in \operatorname {Gr}_{G_\mathbf {F}}$ under right multiplication by ![]() $\textrm {L}^+G_\mathbf {F}$ is
$\textrm {L}^+G_\mathbf {F}$ is ![]() $(\textrm {L}^+G_\mathbf {F} \cap u^{-\mu } \textrm {L}^+G_\mathbf {F} u^\mu )$, and so we get a locally closed immersion
$(\textrm {L}^+G_\mathbf {F} \cap u^{-\mu } \textrm {L}^+G_\mathbf {F} u^\mu )$, and so we get a locally closed immersion
with image ![]() $\operatorname {Gr}_{\mathbf {F}}^{\circ, \mu }$ (cf. the proof of [Reference ZhuZhu17, Proposition 2.1.5]). Right multiplication by
$\operatorname {Gr}_{\mathbf {F}}^{\circ, \mu }$ (cf. the proof of [Reference ZhuZhu17, Proposition 2.1.5]). Right multiplication by ![]() $u^{-\mu }$ gives an isomorphism from the tangent space of
$u^{-\mu }$ gives an isomorphism from the tangent space of ![]() $\operatorname {Gr}_{\mathbf {F}}^{\circ, \mu }$ at
$\operatorname {Gr}_{\mathbf {F}}^{\circ, \mu }$ at ![]() $u^\mu$ to
$u^\mu$ to
In our analysis, the affine Grassmanians that appear will actually be for the group
Assuming ![]() $\Lambda$ is sufficiently large,
$\Lambda$ is sufficiently large, ![]() $G'$ is just a product of
$G'$ is just a product of ![]() $\operatorname {Hom}_{\mathbf {Q}_{p}}(K, L)$-copies of
$\operatorname {Hom}_{\mathbf {Q}_{p}}(K, L)$-copies of ![]() $G$ and so the above discussion applies with
$G$ and so the above discussion applies with ![]() $G$ replaced by
$G$ replaced by ![]() $G'$. Any
$G'$. Any ![]() $\mu \in X_*(T') = X_*(T)^{\operatorname {Hom}(K, L)}$ defines a cocharacter of the
$\mu \in X_*(T') = X_*(T)^{\operatorname {Hom}(K, L)}$ defines a cocharacter of the ![]() $G'$ and an affine Schubert variety
$G'$ and an affine Schubert variety ![]() $\operatorname {Gr}_{G'}^{\leqslant \mu }$.
$\operatorname {Gr}_{G'}^{\leqslant \mu }$.
2.4  $p$-adic Hodge theory
$p$-adic Hodge theory
We briefly review the translation of ![]() $p$-adic Hodge theory to apply to
$p$-adic Hodge theory to apply to ![]() $G$-valued representations; see, for example, [Reference LevinLev15, § 2.4] for details. Let
$G$-valued representations; see, for example, [Reference LevinLev15, § 2.4] for details. Let ![]() $K$ be a finite extension of
$K$ be a finite extension of ![]() $\mathbf {Q}_p$ and
$\mathbf {Q}_p$ and ![]() $\Gamma _K$ be the absolute Galois group of
$\Gamma _K$ be the absolute Galois group of ![]() $K$. For any
$K$. For any ![]() $L$-algebra
$L$-algebra ![]() $B$ and continuous representation
$B$ and continuous representation ![]() $\rho : \Gamma _K \to G(B)$, we say that
$\rho : \Gamma _K \to G(B)$, we say that ![]() $\rho$ is crystalline (respectively, semi-stable, de Rham) if
$\rho$ is crystalline (respectively, semi-stable, de Rham) if ![]() $\rho _V$ is crystalline (respectively, semi-stable, de Rham) for all
$\rho _V$ is crystalline (respectively, semi-stable, de Rham) for all ![]() $V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$. As
$V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$. As ![]() $G$ is reductive, this can be checked on a single faithful representation.
$G$ is reductive, this can be checked on a single faithful representation.
Definition 2.4.1 A ![]() $p$-adic Hodge type for
$p$-adic Hodge type for ![]() $G$ is a geometric conjugacy class of cocharacters of
$G$ is a geometric conjugacy class of cocharacters of ![]() $(\operatorname {Res}_{K \otimes _{\mathbf {Q}_{p}} L /L } G) _{\overline {L}}$.
$(\operatorname {Res}_{K \otimes _{\mathbf {Q}_{p}} L /L } G) _{\overline {L}}$.
A ![]() $p$-adic Hodge type is equivalent to a collection of geometric cocharacters of
$p$-adic Hodge type is equivalent to a collection of geometric cocharacters of ![]() $G_{\overline {L}}$ indexed by
$G_{\overline {L}}$ indexed by ![]() $\mathbf {Q}_{p}$-embeddings of
$\mathbf {Q}_{p}$-embeddings of ![]() $K$ into
$K$ into ![]() $\overline {L}$. For a fixed split maximal torus
$\overline {L}$. For a fixed split maximal torus ![]() $T$ in
$T$ in ![]() $G$, each type can be represented by an element
$G$, each type can be represented by an element ![]() $\mu \in X_*(T)^{\operatorname {Hom}_{\mathbf {Q}_{p}}(K,\overline {L})}$. We denote the conjugacy class by
$\mu \in X_*(T)^{\operatorname {Hom}_{\mathbf {Q}_{p}}(K,\overline {L})}$. We denote the conjugacy class by ![]() $[\mu ]$. When there is no danger of confusion, we often speak of a cocharacter
$[\mu ]$. When there is no danger of confusion, we often speak of a cocharacter ![]() $\mu$ of
$\mu$ of ![]() $G$ being a
$G$ being a ![]() $p$-adic Hodge type (or just a type) instead of the geometric conjugacy class.
$p$-adic Hodge type (or just a type) instead of the geometric conjugacy class.
The functor ![]() $D_{\operatorname {dR}}$ from the category of de Rham representations on projective
$D_{\operatorname {dR}}$ from the category of de Rham representations on projective ![]() $B$-modules to the category of filtered
$B$-modules to the category of filtered ![]() $K \otimes _{\mathbf {Q}_{p}} B$-modules is a tensor exact functor. For a de Rham
$K \otimes _{\mathbf {Q}_{p}} B$-modules is a tensor exact functor. For a de Rham ![]() $\rho : \Gamma _K \to G(B)$, composing with
$\rho : \Gamma _K \to G(B)$, composing with ![]() $D_{\operatorname {dR}}$ defines a tensor-exact functor from
$D_{\operatorname {dR}}$ defines a tensor-exact functor from ![]() ${^f} \hspace {-2pt} \operatorname {Rep}_L(G_L)$ to
${^f} \hspace {-2pt} \operatorname {Rep}_L(G_L)$ to ![]() $\operatorname {Fil}_{K \otimes _{\mathbf {Q}_{p}} B}$ which we denote by
$\operatorname {Fil}_{K \otimes _{\mathbf {Q}_{p}} B}$ which we denote by ![]() $\mathcal {F}_{\rho }^{\operatorname {dR}}$. Let
$\mathcal {F}_{\rho }^{\operatorname {dR}}$. Let ![]() $[\mu ]$ be a
$[\mu ]$ be a ![]() $p$-adic Hodge type for
$p$-adic Hodge type for ![]() $G$. We say that
$G$. We say that ![]() $\rho$ has type
$\rho$ has type ![]() $[\mu ]$ provided that
$[\mu ]$ provided that ![]() $\mathcal {F}_{\rho }^{\operatorname {dR}}$ has type
$\mathcal {F}_{\rho }^{\operatorname {dR}}$ has type ![]() $[\mu ]$.
$[\mu ]$.
Now fix a continuous ![]() ${\overline {\rho }} : \Gamma _K \to G(\mathbf {F})$. There are framed deformation rings whose characteristic zero points incorporate conditions from
${\overline {\rho }} : \Gamma _K \to G(\mathbf {F})$. There are framed deformation rings whose characteristic zero points incorporate conditions from ![]() $p$-adic Hodge theory.
$p$-adic Hodge theory.
Fact 2.4.2 Let ![]() $\mu$ be a
$\mu$ be a ![]() $p$-adic Hodge type of
$p$-adic Hodge type of ![]() $G$ and
$G$ and ![]() $R_{{\overline {\rho }}}^{\mu,\square }$ be the framed crystalline deformation ring for
$R_{{\overline {\rho }}}^{\mu,\square }$ be the framed crystalline deformation ring for ![]() ${\overline {\rho }}$ with
${\overline {\rho }}$ with ![]() $p$-adic Hodge type
$p$-adic Hodge type ![]() $\mu$. It is a complete local
$\mu$. It is a complete local ![]() $\Lambda$-algebra which is
$\Lambda$-algebra which is ![]() $\Lambda$-flat and reduced. Its relative dimension over
$\Lambda$-flat and reduced. Its relative dimension over ![]() $\Lambda$ is
$\Lambda$ is ![]() $\dim G_{\mathbf {F}} + \dim P_{\mu, \mathbf {F}} \backslash G'_{\mathbf {F}}$.
$\dim G_{\mathbf {F}} + \dim P_{\mu, \mathbf {F}} \backslash G'_{\mathbf {F}}$.
The ring ![]() $R_{{\overline {\rho }}}^{\mu, \square }$ is the flat closure of the locus in
$R_{{\overline {\rho }}}^{\mu, \square }$ is the flat closure of the locus in ![]() $(R^{\square }_{{\overline {\rho }}}[1/p])$ of crystalline representations with
$(R^{\square }_{{\overline {\rho }}}[1/p])$ of crystalline representations with ![]() $p$-adic Hodge type
$p$-adic Hodge type ![]() $\mu$ constructed in [Reference BalajiBal12, Theorem 4.0.12]. More precisely, for a finite local
$\mu$ constructed in [Reference BalajiBal12, Theorem 4.0.12]. More precisely, for a finite local ![]() $L$-algebra
$L$-algebra ![]() $A$, an
$A$, an ![]() $A$-valued point of
$A$-valued point of ![]() $R_{{\overline {\rho }}}^{\square }$ factors through
$R_{{\overline {\rho }}}^{\square }$ factors through ![]() $R_{{\overline {\rho }}}^{\mu,\square }$ if and only if the associated Galois representation is crystalline with
$R_{{\overline {\rho }}}^{\mu,\square }$ if and only if the associated Galois representation is crystalline with ![]() $p$-adic Hodge type
$p$-adic Hodge type ![]() $\mu$. Since the local rings of the generic fiber
$\mu$. Since the local rings of the generic fiber ![]() $(R_{{\overline {\rho }}}^{\mu,\square }[1/p])$ are formally smooth, the generic fiber is reduced. Since
$(R_{{\overline {\rho }}}^{\mu,\square }[1/p])$ are formally smooth, the generic fiber is reduced. Since ![]() $R_{{\overline {\rho }}}^{\mu,\square }$ is
$R_{{\overline {\rho }}}^{\mu,\square }$ is ![]() $\Lambda$-flat by construction, it is also reduced. The relative dimension comes from a calculation of the dimension of the generic fiber [Reference BalajiBal12, Theorem 5.1.5].
$\Lambda$-flat by construction, it is also reduced. The relative dimension comes from a calculation of the dimension of the generic fiber [Reference BalajiBal12, Theorem 5.1.5].
3. Deformations of  $G$-Kisin modules and Galois representations
$G$-Kisin modules and Galois representations
Fix a ![]() $p$-adic field
$p$-adic field ![]() $K$ unramified over
$K$ unramified over ![]() $\mathbf {Q}_p$ with residue field
$\mathbf {Q}_p$ with residue field ![]() $k$ and ring of integers
$k$ and ring of integers ![]() $W(k)$. Let
$W(k)$. Let ![]() $\Gamma _K$ denote the absolute Galois group of
$\Gamma _K$ denote the absolute Galois group of ![]() $K$ with respect to a fixed algebraic closure
$K$ with respect to a fixed algebraic closure ![]() $\overline {K}$. As before, let
$\overline {K}$. As before, let ![]() $\Lambda$ be the ring of integers in a
$\Lambda$ be the ring of integers in a ![]() $p$-adic field
$p$-adic field ![]() $L$ with residue field
$L$ with residue field ![]() $\mathbf {F}$, and
$\mathbf {F}$, and ![]() $G$ be a split reductive group defined over
$G$ be a split reductive group defined over ![]() $\Lambda$. Assume
$\Lambda$. Assume ![]() $L$ is sufficiently large such that it contains a copy of
$L$ is sufficiently large such that it contains a copy of ![]() $K$. Throughout this section, we also assume that
$K$. Throughout this section, we also assume that ![]() $p \nmid \# \pi _1(G^{\operatorname {der}})$.
$p \nmid \# \pi _1(G^{\operatorname {der}})$.
3.1  $G$-Kisin modules and types
$G$-Kisin modules and types
We begin by recalling the definition of a Kisin module with ![]() $G$-structure and some related notions from [Reference LevinLev15, § 2.2]. These are generalizations of the objects introduced in [Reference KisinKis09], which addressed the case that
$G$-structure and some related notions from [Reference LevinLev15, § 2.2]. These are generalizations of the objects introduced in [Reference KisinKis09], which addressed the case that ![]() $G = \operatorname {GL}_n$. We work with
$G = \operatorname {GL}_n$. We work with ![]() $p$-adically complete
$p$-adically complete ![]() $\Lambda$-algebras
$\Lambda$-algebras ![]() $A$, and use the ring
$A$, and use the ring ![]() $\mathfrak {S}_A$ equipped with Frobenius
$\mathfrak {S}_A$ equipped with Frobenius ![]() $\varphi$ introduced in § 1.3.5. We continue to work with
$\varphi$ introduced in § 1.3.5. We continue to work with ![]() $G$-bundles in the fppf topology.
$G$-bundles in the fppf topology.
Definition 3.1.1 For a ![]() $p$-adically complete
$p$-adically complete ![]() $\Lambda$-algebra
$\Lambda$-algebra ![]() $A$, a
$A$, a ![]() $G$-Kisin module with coefficients in
$G$-Kisin module with coefficients in ![]() $A$ is a pair
$A$ is a pair ![]() $(\mathfrak {P}, \phi _{\mathfrak {P}})$ where
$(\mathfrak {P}, \phi _{\mathfrak {P}})$ where ![]() $\mathfrak {P}$ is a
$\mathfrak {P}$ is a ![]() $G$-bundle on
$G$-bundle on ![]() $\operatorname {Spec} \mathfrak {S}_A$ and
$\operatorname {Spec} \mathfrak {S}_A$ and ![]() $\phi _{\mathfrak {P}}: \varphi ^*(\mathfrak {P})[1/ E(u)] \simeq \mathfrak {P}[1/E(u)]$ is an isomorphism of
$\phi _{\mathfrak {P}}: \varphi ^*(\mathfrak {P})[1/ E(u)] \simeq \mathfrak {P}[1/E(u)]$ is an isomorphism of ![]() $G$-bundles.
$G$-bundles.
We often suppress ![]() $\phi _\mathfrak {P}$ and speak of
$\phi _\mathfrak {P}$ and speak of ![]() $\mathfrak {P}$ as being a
$\mathfrak {P}$ as being a ![]() $G$-Kisin module (denoting
$G$-Kisin module (denoting ![]() $\phi _\mathfrak {P}$ by
$\phi _\mathfrak {P}$ by ![]() $\phi$ if the subscript is not necessary to disambiguate).
$\phi$ if the subscript is not necessary to disambiguate).
Definition 3.1.2 When ![]() $G = \operatorname {GL}(V)$ where
$G = \operatorname {GL}(V)$ where ![]() $V$ is finite free over
$V$ is finite free over ![]() $\Lambda$, a
$\Lambda$, a ![]() $G$-Kisin module with coefficients in
$G$-Kisin module with coefficients in ![]() $A$ is equivalent to a finitely generated projective module
$A$ is equivalent to a finitely generated projective module ![]() $\mathfrak {M}$ over
$\mathfrak {M}$ over ![]() $\mathfrak {S}_A$ of rank equal to the rank of
$\mathfrak {S}_A$ of rank equal to the rank of ![]() $V$, together with an isomorphism
$V$, together with an isomorphism ![]() $\phi _{\mathfrak {M}}:\varphi ^*(\mathfrak {M})[1/ E(u)] \simeq \mathfrak {M}[1/E(u)]$. Let
$\phi _{\mathfrak {M}}:\varphi ^*(\mathfrak {M})[1/ E(u)] \simeq \mathfrak {M}[1/E(u)]$. Let ![]() $a \leqslant b$ be integers. We say that
$a \leqslant b$ be integers. We say that ![]() $\mathfrak {M}$ has height in
$\mathfrak {M}$ has height in ![]() $[a, b]$ if
$[a, b]$ if
We say ![]() $\mathfrak {M}$ has bounded height if it has height in
$\mathfrak {M}$ has bounded height if it has height in ![]() $[a, b]$ for some integers
$[a, b]$ for some integers ![]() $a$ and
$a$ and ![]() $b$.
$b$.
Remark 3.1.3 In the case of ![]() $\operatorname {GL}(V)$, there is often an effectivity condition which corresponds to
$\operatorname {GL}(V)$, there is often an effectivity condition which corresponds to ![]() $a \geqslant 0$, but there is no such notion for
$a \geqslant 0$, but there is no such notion for ![]() $G$-bundles since all
$G$-bundles since all ![]() $G$-bundle maps are isomorphisms.
$G$-bundle maps are isomorphisms.
Example 3.1.4 For any representation ![]() $V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$, one can pushout a
$V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$, one can pushout a ![]() $G$-Kisin module
$G$-Kisin module ![]() $\mathfrak {P}$ with coefficients in
$\mathfrak {P}$ with coefficients in ![]() $A$ to a
$A$ to a ![]() $\operatorname {GL}(V)$-Kisin module, which we denote by
$\operatorname {GL}(V)$-Kisin module, which we denote by ![]() $\mathfrak {P}(V)$. This construction gives an equivalence between
$\mathfrak {P}(V)$. This construction gives an equivalence between ![]() $G$-Kisin modules and faithful, exact tensor functor from
$G$-Kisin modules and faithful, exact tensor functor from ![]() ${^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$ to the category of Kisin modules with bounded height. More precisely, a
${^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$ to the category of Kisin modules with bounded height. More precisely, a ![]() $G$-Kisin module is equivalent to the data of a fiber functor
$G$-Kisin module is equivalent to the data of a fiber functor ![]() $\eta$ corresponding to the underlying
$\eta$ corresponding to the underlying ![]() $G$-bundle plus the data of isomorphisms
$G$-bundle plus the data of isomorphisms
for each ![]() $V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$ that are compatible with exact sequences and tensor products.
$V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$ that are compatible with exact sequences and tensor products.
Example 3.1.5 Let ![]() $\mathfrak {P}$ be a
$\mathfrak {P}$ be a ![]() $G$-Kisin module with coefficients in
$G$-Kisin module with coefficients in ![]() $A$. If
$A$. If ![]() $\mathfrak {P}$ is a trivial
$\mathfrak {P}$ is a trivial ![]() $G$-bundle (this is equivalent to
$G$-bundle (this is equivalent to ![]() $\mathfrak {P} \mod u$ being trivial) and if one chooses a trivialization
$\mathfrak {P} \mod u$ being trivial) and if one chooses a trivialization ![]() $\beta$, then we can associate to
$\beta$, then we can associate to ![]() $\phi _{\mathfrak {P}}$ an element
$\phi _{\mathfrak {P}}$ an element ![]() $C_{\mathfrak {P}, \beta } \in G(\mathfrak {S}_A[1/E(u)])$. Changing trivialization by an element
$C_{\mathfrak {P}, \beta } \in G(\mathfrak {S}_A[1/E(u)])$. Changing trivialization by an element ![]() $D \in G(\mathfrak {S}_A)$ replaces
$D \in G(\mathfrak {S}_A)$ replaces ![]() $C_{\mathfrak {P}, \beta }$ by its
$C_{\mathfrak {P}, \beta }$ by its ![]() $\varphi$-conjugate
$\varphi$-conjugate ![]() $D C_{\mathfrak {P}, \beta } \varphi (D)^{-1}$.
$D C_{\mathfrak {P}, \beta } \varphi (D)^{-1}$.
Recall that ![]() $G' = \operatorname {Res}_{(W(k) \otimes _{\mathbf {Z}_p} \Lambda )/ \Lambda } G$. By assumption,
$G' = \operatorname {Res}_{(W(k) \otimes _{\mathbf {Z}_p} \Lambda )/ \Lambda } G$. By assumption, ![]() $L$ contains a copy of
$L$ contains a copy of ![]() $K$, and so
$K$, and so ![]() $G' = \prod _{\sigma \in \operatorname {Hom}(K, L)} G$. A cocharacter
$G' = \prod _{\sigma \in \operatorname {Hom}(K, L)} G$. A cocharacter ![]() $\mu$ of
$\mu$ of ![]() $G'$ is equivalent to a collection
$G'$ is equivalent to a collection ![]() $(\mu _{\sigma })_{\sigma \in \operatorname {Hom}(K, L)}$ where each
$(\mu _{\sigma })_{\sigma \in \operatorname {Hom}(K, L)}$ where each ![]() $\mu _{\sigma }$ is a cocharacter of
$\mu _{\sigma }$ is a cocharacter of ![]() $G$.
$G$.
As we have assumed that ![]() $p \nmid \# \pi _1(G^{\operatorname {der}})$, we have an affine Schubert variety
$p \nmid \# \pi _1(G^{\operatorname {der}})$, we have an affine Schubert variety ![]() $\operatorname {Gr}^{\leqslant \mu }_{G'}$ associated to
$\operatorname {Gr}^{\leqslant \mu }_{G'}$ associated to ![]() $\mu$ over
$\mu$ over ![]() $\Lambda$ as in § 2.3. It is projective,
$\Lambda$ as in § 2.3. It is projective, ![]() $\Lambda$-flat, and stable under right multiplication by
$\Lambda$-flat, and stable under right multiplication by ![]() $\textrm {L}^+G'$. As the notation suggests, the special fiber of
$\textrm {L}^+G'$. As the notation suggests, the special fiber of ![]() $\operatorname {Gr}_{G'}^{\leqslant \mu }$ is the affine Schubert variety
$\operatorname {Gr}_{G'}^{\leqslant \mu }$ is the affine Schubert variety ![]() $\operatorname {Gr}_{G'_{\mathbf {F}}}^{\leqslant \mu }$.
$\operatorname {Gr}_{G'_{\mathbf {F}}}^{\leqslant \mu }$.
Let ![]() $\mathfrak {P}$ be a
$\mathfrak {P}$ be a ![]() $G$-Kisin module with coefficients in a
$G$-Kisin module with coefficients in a ![]() $p$-adically complete
$p$-adically complete ![]() $\Lambda$-algebra
$\Lambda$-algebra ![]() $A$ together with a trivialization
$A$ together with a trivialization ![]() $\beta$. The Frobenius then defines an element
$\beta$. The Frobenius then defines an element ![]() $C_{\mathfrak {P}, \beta } \in G(\mathfrak {S}_A[1/E(u)])$. Since
$C_{\mathfrak {P}, \beta } \in G(\mathfrak {S}_A[1/E(u)])$. Since ![]() $A$ is
$A$ is ![]() $p$-adically complete,
$p$-adically complete, ![]() $\mathfrak {S}_A = (W(k) \otimes A)[\![u]\!] = (W(k) \otimes A)[\![u - p]\!]$ and so
$\mathfrak {S}_A = (W(k) \otimes A)[\![u]\!] = (W(k) \otimes A)[\![u - p]\!]$ and so ![]() $G(\mathfrak {S}_A[1/E(u)]) = \operatorname {LG}' (A)$. Letting
$G(\mathfrak {S}_A[1/E(u)]) = \operatorname {LG}' (A)$. Letting ![]() $[C_{\mathfrak {P}, \beta }]$ denote the class of
$[C_{\mathfrak {P}, \beta }]$ denote the class of ![]() $C_{\mathfrak {P}, \beta }$ in the quotient
$C_{\mathfrak {P}, \beta }$ in the quotient ![]() $\textrm {L}^+G'(A) \backslash \operatorname {LG}' (A)$, the map
$\textrm {L}^+G'(A) \backslash \operatorname {LG}' (A)$, the map ![]() $(\mathfrak {P}, \beta ) \mapsto [C_{\mathfrak {P}, \beta }]$ defines an element
$(\mathfrak {P}, \beta ) \mapsto [C_{\mathfrak {P}, \beta }]$ defines an element ![]() $\Psi (\mathfrak {P}, \beta )$ of
$\Psi (\mathfrak {P}, \beta )$ of ![]() $\operatorname {Gr}_{G'}(A)$.
$\operatorname {Gr}_{G'}(A)$.
Example 3.1.6 As we assume that ![]() $L$ is sufficiently large to contain a copy of
$L$ is sufficiently large to contain a copy of ![]() $K$, we can be more explicit. Letting
$K$, we can be more explicit. Letting ![]() $\mathcal {J}$ be the set of embeddings of
$\mathcal {J}$ be the set of embeddings of ![]() $W(k)$ into
$W(k)$ into ![]() $\Lambda$, we see
$\Lambda$, we see
Thus, we may represent ![]() $C_{\mathfrak {P},\beta }$ as a tuple
$C_{\mathfrak {P},\beta }$ as a tuple ![]() $(C^{\sigma }_{\mathfrak {P},\beta })_{\sigma \in \mathcal {J}}$. Note that
$(C^{\sigma }_{\mathfrak {P},\beta })_{\sigma \in \mathcal {J}}$. Note that ![]() $\varphi (C_{\mathfrak {P},\beta }) = ( \varphi (C^{\sigma \varphi ^{-1}}_{\mathfrak {P},\beta })) _{\sigma \in \mathcal {J}}$.
$\varphi (C_{\mathfrak {P},\beta }) = ( \varphi (C^{\sigma \varphi ^{-1}}_{\mathfrak {P},\beta })) _{\sigma \in \mathcal {J}}$.
Definition 3.1.7 Let ![]() $\mathfrak {P}$ be a
$\mathfrak {P}$ be a ![]() $G$-Kisin module with coefficients in a
$G$-Kisin module with coefficients in a ![]() $p$-adically complete
$p$-adically complete ![]() $\Lambda$-algebra
$\Lambda$-algebra ![]() $A$. Assume
$A$. Assume ![]() $\mathfrak {P}$ admits a trivialization
$\mathfrak {P}$ admits a trivialization ![]() $\beta$. We say
$\beta$. We say ![]() $\mathfrak {P}$ has type
$\mathfrak {P}$ has type ![]() $\leqslant \mu$ if
$\leqslant \mu$ if ![]() $\Psi (\mathfrak {P}, \beta ) \in \operatorname {Gr}^{\leqslant \mu }_{G'}(A)$. Note that this condition does not depend on the choice of trivialization because
$\Psi (\mathfrak {P}, \beta ) \in \operatorname {Gr}^{\leqslant \mu }_{G'}(A)$. Note that this condition does not depend on the choice of trivialization because ![]() $\operatorname {Gr}^{\leqslant \mu }_{G'}$ is stable under right multiplication by
$\operatorname {Gr}^{\leqslant \mu }_{G'}$ is stable under right multiplication by ![]() $\textrm {L}^+G'$. Let
$\textrm {L}^+G'$. Let ![]() $Y^{\leqslant \mu }(A)$ denote the category of
$Y^{\leqslant \mu }(A)$ denote the category of ![]() $G$-Kisin modules with coefficients in
$G$-Kisin modules with coefficients in ![]() $A$ and type
$A$ and type ![]() $\leqslant \mu$.
$\leqslant \mu$.
The following elementary observation is key to many computations.
Lemma 3.1.8 Let ![]() $\mathfrak {P}$ be a
$\mathfrak {P}$ be a ![]() $G$-Kisin module of type
$G$-Kisin module of type ![]() $\leqslant \mu$ with coefficients in a
$\leqslant \mu$ with coefficients in a ![]() $p$-adically complete
$p$-adically complete ![]() $\Lambda$-algebra
$\Lambda$-algebra ![]() $A$. Then
$A$. Then ![]() $\mathfrak {P}(\operatorname {Lie} G)$ has height in
$\mathfrak {P}(\operatorname {Lie} G)$ has height in ![]() $[-h_{\mu }, h_{\mu }]$, where
$[-h_{\mu }, h_{\mu }]$, where ![]() $h_{\mu } = \max _{\alpha \in \Phi _{G'}} \langle \mu,\alpha \rangle$.
$h_{\mu } = \max _{\alpha \in \Phi _{G'}} \langle \mu,\alpha \rangle$.
Proof. This follows from considering the adjoint representation.
If ![]() $\mathfrak {P}$ has coefficients in
$\mathfrak {P}$ has coefficients in ![]() $\mathbf {F}$, then
$\mathbf {F}$, then ![]() $\mathfrak {P}$ has type
$\mathfrak {P}$ has type ![]() $\leqslant \mu$ if and only if for some
$\leqslant \mu$ if and only if for some ![]() $\mu ' \leqslant \mu$ and choice of trivialization
$\mu ' \leqslant \mu$ and choice of trivialization ![]() $\beta$,
$\beta$, ![]() $C_{\mathfrak {P}, \beta } \in L^+ G'(\mathbf {F}) u^{\mu '} L^+ G'(\mathbf {F})$ (see Remark 2.3.2). We give this element a name following [Reference Le, Le Hung, Levin and MorraLLHLM18].
$C_{\mathfrak {P}, \beta } \in L^+ G'(\mathbf {F}) u^{\mu '} L^+ G'(\mathbf {F})$ (see Remark 2.3.2). We give this element a name following [Reference Le, Le Hung, Levin and MorraLLHLM18].
Definition 3.1.9 Let ![]() $\mathfrak {P}$ be a
$\mathfrak {P}$ be a ![]() $G$-Kisin module with coefficient in
$G$-Kisin module with coefficient in ![]() $\mathbf {F}$ and
$\mathbf {F}$ and ![]() $\mu '$ a dominant cocharacter of
$\mu '$ a dominant cocharacter of ![]() $G'$. We say that
$G'$. We say that ![]() $\mathfrak {P}$ has shape
$\mathfrak {P}$ has shape ![]() $\mu '$ provided that for any choice of trivialization
$\mu '$ provided that for any choice of trivialization ![]() $\beta$ we have
$\beta$ we have ![]() $C_{\mathfrak {P}, \beta } \in L^+ G'(\mathbf {F}) u^{\mu '} L^+ G'(\mathbf {F})$.
$C_{\mathfrak {P}, \beta } \in L^+ G'(\mathbf {F}) u^{\mu '} L^+ G'(\mathbf {F})$.
3.2  $G$-Kisin modules and Galois representations
$G$-Kisin modules and Galois representations
The connection between ![]() $G$-Kisin modules and Galois representation is via the theory of étale
$G$-Kisin modules and Galois representation is via the theory of étale ![]() $\varphi$-modules, which uses the rings
$\varphi$-modules, which uses the rings ![]() $\mathcal {O}_{\mathcal {E},A}$ with Frobenius
$\mathcal {O}_{\mathcal {E},A}$ with Frobenius ![]() $\varphi$ recalled in § 1.3.5.
$\varphi$ recalled in § 1.3.5.
Definition 3.2.1 For a ![]() $p$-adically complete
$p$-adically complete ![]() $\Lambda$-algebra
$\Lambda$-algebra ![]() $A$, a
$A$, a ![]() $(\mathcal {O}_{\mathcal {E},A},\varphi )$-module with
$(\mathcal {O}_{\mathcal {E},A},\varphi )$-module with ![]() $G$-structure with coefficients in
$G$-structure with coefficients in ![]() $A$ is a pair
$A$ is a pair ![]() $(P,\phi _P)$ where
$(P,\phi _P)$ where ![]() $P$ is a
$P$ is a ![]() $G$-bundle on
$G$-bundle on ![]() $\operatorname {Spec} \mathcal {O}_{\mathcal {E},A}$ and
$\operatorname {Spec} \mathcal {O}_{\mathcal {E},A}$ and ![]() $\phi _P : \varphi ^*(P) \to P$ is an isomorphism. We denote the category of such pairs by
$\phi _P : \varphi ^*(P) \to P$ is an isomorphism. We denote the category of such pairs by ![]() $\operatorname {GMod}_{\mathcal {O}_{\mathcal {E},A}}^{\varphi }$.
$\operatorname {GMod}_{\mathcal {O}_{\mathcal {E},A}}^{\varphi }$.
Example 3.2.2 An element ![]() $(P,\Phi _P) \in \operatorname {GMod}^\varphi _{\mathcal {O}_{\mathcal {E},A}}$ is equivalent to a faithful, exact tensor functor from
$(P,\Phi _P) \in \operatorname {GMod}^\varphi _{\mathcal {O}_{\mathcal {E},A}}$ is equivalent to a faithful, exact tensor functor from ![]() ${^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$ to the category of
${^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$ to the category of ![]() $(\mathcal {O}_{\mathcal {E},A},\varphi )$-modules.
$(\mathcal {O}_{\mathcal {E},A},\varphi )$-modules.
Since ![]() $E(u)$ is invertible in
$E(u)$ is invertible in ![]() $\mathcal {O}_{\mathcal {E}}$, there is a natural map
$\mathcal {O}_{\mathcal {E}}$, there is a natural map ![]() $\mathfrak {S}_A[1/E(u)] \to \mathcal {O}_{\mathcal {E},A}$ for any
$\mathfrak {S}_A[1/E(u)] \to \mathcal {O}_{\mathcal {E},A}$ for any ![]() $p$-adically complete
$p$-adically complete ![]() $\Lambda$-algebra
$\Lambda$-algebra ![]() $A$. We let
$A$. We let ![]() $\epsilon _G$ denote the induced functor from the category of
$\epsilon _G$ denote the induced functor from the category of ![]() $G$-Kisin modules with coefficients in
$G$-Kisin modules with coefficients in ![]() $A$ to the category of
$A$ to the category of ![]() $(\mathcal {O}_{\mathcal {E},A},\varphi )$-modules with
$(\mathcal {O}_{\mathcal {E},A},\varphi )$-modules with ![]() $G$-structure.
$G$-structure.
Definition 3.2.3 Let ![]() $A$ be a
$A$ be a ![]() $p$-adically complete
$p$-adically complete ![]() $\Lambda$-algebra and
$\Lambda$-algebra and ![]() $P \in \operatorname {GMod}_{\mathcal {O}_{\mathcal {E},A}}^{\varphi }$. A
$P \in \operatorname {GMod}_{\mathcal {O}_{\mathcal {E},A}}^{\varphi }$. A ![]() $G$-Kisin lattice of
$G$-Kisin lattice of ![]() $P$ is a
$P$ is a ![]() $G$-Kisin lattice inside
$G$-Kisin lattice inside ![]() $P$, i.e. a
$P$, i.e. a ![]() $G$-Kisin module
$G$-Kisin module ![]() $\mathfrak {P}$ with coefficients in
$\mathfrak {P}$ with coefficients in ![]() $A$ together with an isomorphism
$A$ together with an isomorphism ![]() $\alpha : \epsilon _G(\mathfrak {P}) \simeq P$ (compatible with
$\alpha : \epsilon _G(\mathfrak {P}) \simeq P$ (compatible with ![]() $\phi _{\mathfrak {P}}$ and
$\phi _{\mathfrak {P}}$ and ![]() $\phi _{P}$).
$\phi _{P}$).
The category ![]() $\operatorname {GMod}_{\mathcal {O}_{\mathcal {E},A}}^{\varphi }$ is connected with
$\operatorname {GMod}_{\mathcal {O}_{\mathcal {E},A}}^{\varphi }$ is connected with ![]() $G$-valued Galois representations. As in § 1.3.4, fix a compatible system
$G$-valued Galois representations. As in § 1.3.4, fix a compatible system ![]() $\{p^{1/p}, p^{1/p^2}, \ldots \}$ of
$\{p^{1/p}, p^{1/p^2}, \ldots \}$ of ![]() $p$-power roots of
$p$-power roots of ![]() $p$, and let
$p$, and let ![]() $K_\infty = K(p^{1/p}, p^{1/p^2}, \ldots )$ and
$K_\infty = K(p^{1/p}, p^{1/p^2}, \ldots )$ and ![]() $\Gamma _\infty = \operatorname {Gal}(\overline {K}/ K_\infty )$. The following result is [Reference LevinLev15, Proposition 2.2.4].
$\Gamma _\infty = \operatorname {Gal}(\overline {K}/ K_\infty )$. The following result is [Reference LevinLev15, Proposition 2.2.4].
Fact 3.2.4 For a ![]() $\Lambda$-algebra
$\Lambda$-algebra ![]() $A$ which is finite over
$A$ which is finite over ![]() $\mathbf {Z}_p$ and either
$\mathbf {Z}_p$ and either ![]() $\mathbf {Z}_p$-flat or Artinian, there is a functor
$\mathbf {Z}_p$-flat or Artinian, there is a functor ![]() $T_{G,A} : \operatorname {GMod}_{\mathcal {O}_{\mathcal {E},A}}^{\varphi } \to \operatorname {GRep}_A(\Gamma _\infty )$ giving an equivalence of categories with quasi-inverse
$T_{G,A} : \operatorname {GMod}_{\mathcal {O}_{\mathcal {E},A}}^{\varphi } \to \operatorname {GRep}_A(\Gamma _\infty )$ giving an equivalence of categories with quasi-inverse ![]() $M_{G,A}$.
$M_{G,A}$.
Definition 3.2.5 Let ![]() $\widetilde {T}_{G,A}$ be the composition of
$\widetilde {T}_{G,A}$ be the composition of ![]() $T_{G,A}$ with
$T_{G,A}$ with ![]() $\epsilon _G$.
$\epsilon _G$.
3.3 Deformation problems
We define a variety of deformation problems on the categories ![]() $\mathcal {C}_{\Lambda }$ and
$\mathcal {C}_{\Lambda }$ and ![]() $\widehat {\mathcal {C}}_{\Lambda }$ of coefficient
$\widehat {\mathcal {C}}_{\Lambda }$ of coefficient ![]() $\Lambda$-algebras from § 1.3.7. Subscripts (such as
$\Lambda$-algebras from § 1.3.7. Subscripts (such as ![]() $\overline {\mathfrak {P}}$ or
$\overline {\mathfrak {P}}$ or ![]() ${\overline {\rho }}$) denote the basic objects being deformed, whereas superscripts (such as
${\overline {\rho }}$) denote the basic objects being deformed, whereas superscripts (such as ![]() $\leqslant \mu$ or
$\leqslant \mu$ or ![]() $\square$) impose conditions or specify auxiliary information to be included.
$\square$) impose conditions or specify auxiliary information to be included.
We fix a faithful representation ![]() $V_0 \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$. Let
$V_0 \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$. Let ![]() $\overline {\mathfrak {P}}$ be a
$\overline {\mathfrak {P}}$ be a ![]() $G$-Kisin module with coefficients in
$G$-Kisin module with coefficients in ![]() $\mathbf {F}$, and fix a dominant cocharacter
$\mathbf {F}$, and fix a dominant cocharacter ![]() $\mu$ for
$\mu$ for ![]() $G'$. For any integers
$G'$. For any integers ![]() $a \leqslant b$, we can define a deformation groupoid
$a \leqslant b$, we can define a deformation groupoid ![]() $D^{[a,b]}_{\overline {\mathfrak {P}}}$ on
$D^{[a,b]}_{\overline {\mathfrak {P}}}$ on ![]() $\mathcal {C}_{\Lambda }$ consisting of deformations
$\mathcal {C}_{\Lambda }$ consisting of deformations ![]() $\mathfrak {P}$ of
$\mathfrak {P}$ of ![]() $\overline {\mathfrak {P}}$ such that
$\overline {\mathfrak {P}}$ such that ![]() $\mathfrak {P}(V_0)$ has height in
$\mathfrak {P}(V_0)$ has height in ![]() $[a, b]$. Choosing
$[a, b]$. Choosing ![]() $a$ sufficiently small and
$a$ sufficiently small and ![]() $b$ sufficiently large depending on
$b$ sufficiently large depending on ![]() $\mu$, Levin [Reference LevinLev15, Proposition 3.3.9] constructed a closed subgroupoid
$\mu$, Levin [Reference LevinLev15, Proposition 3.3.9] constructed a closed subgroupoid ![]() $D^{\leqslant \mu }_{\overline {\mathfrak {P}}} \subset D^{[a,b]}_{\overline {\mathfrak {P}}}$ consisting of deformations with type
$D^{\leqslant \mu }_{\overline {\mathfrak {P}}} \subset D^{[a,b]}_{\overline {\mathfrak {P}}}$ consisting of deformations with type ![]() $\leqslant \mu$ (in [Reference LevinLev15] it is denoted by
$\leqslant \mu$ (in [Reference LevinLev15] it is denoted by ![]() $D^{\mu }_{\overline {\mathfrak {P}}}$ but we find
$D^{\mu }_{\overline {\mathfrak {P}}}$ but we find ![]() $\leqslant \mu$ to be more descriptive here). It is non-trivial if and only if
$\leqslant \mu$ to be more descriptive here). It is non-trivial if and only if ![]() $\overline {\mathfrak {P}}$ has type
$\overline {\mathfrak {P}}$ has type ![]() $\leqslant \mu$.
$\leqslant \mu$.
We begin with recalling the construction of representable formally smooth covers of both ![]() $D^{\leqslant \mu }_{\overline {\mathfrak {P}}}$ and
$D^{\leqslant \mu }_{\overline {\mathfrak {P}}}$ and ![]() $D^{[a,b]}_{\overline {\mathfrak {P}}}$ from [Reference LevinLev15, Proposition 3.1.1]. Fix
$D^{[a,b]}_{\overline {\mathfrak {P}}}$ from [Reference LevinLev15, Proposition 3.1.1]. Fix ![]() $N > ({b-a})/({p-1})$ and a trivialization
$N > ({b-a})/({p-1})$ and a trivialization ![]() $\overline {\beta }$ of
$\overline {\beta }$ of ![]() $\overline {\mathfrak {P}}$ mod
$\overline {\mathfrak {P}}$ mod ![]() $E(u)^N$.
$E(u)^N$.
Definition 3.3.1 Define ![]() $D^{\leqslant \mu, \beta }_{\overline {\mathfrak {P}}}(A)$ to be the category of pairs
$D^{\leqslant \mu, \beta }_{\overline {\mathfrak {P}}}(A)$ to be the category of pairs ![]() $(\mathfrak {P}, \beta )$ where
$(\mathfrak {P}, \beta )$ where ![]() $D^{\leqslant \mu }_{\overline {\mathfrak {P}}}(A)$ and
$D^{\leqslant \mu }_{\overline {\mathfrak {P}}}(A)$ and ![]() $\beta$ is a trivialization of
$\beta$ is a trivialization of ![]() $\mathfrak {P}\!\! \mod E(u)^N$ lifting
$\mathfrak {P}\!\! \mod E(u)^N$ lifting ![]() $\overline {\beta }$. (It is denoted by
$\overline {\beta }$. (It is denoted by ![]() $\widetilde {D}_{\overline {\mathfrak {P}}}^{(N), \mu }$ in [Reference LevinLev15].)
$\widetilde {D}_{\overline {\mathfrak {P}}}^{(N), \mu }$ in [Reference LevinLev15].)
Here ![]() $D^{\leqslant \mu, \beta }_{\overline {\mathfrak {P}}}$ is representable on
$D^{\leqslant \mu, \beta }_{\overline {\mathfrak {P}}}$ is representable on ![]() $\widehat {\mathcal {C}}_{\Lambda }$ by a complete local Noetherian ring which we denote by
$\widehat {\mathcal {C}}_{\Lambda }$ by a complete local Noetherian ring which we denote by ![]() $R_{\overline {\mathfrak {P}}}^{\leqslant \mu,\beta }$. Now fix a continuous Galois representation
$R_{\overline {\mathfrak {P}}}^{\leqslant \mu,\beta }$. Now fix a continuous Galois representation ![]() ${\overline {\rho }}: \Gamma _K \to G(\mathbf {F})$. We will define some additional deformation functors assuming there exists a
${\overline {\rho }}: \Gamma _K \to G(\mathbf {F})$. We will define some additional deformation functors assuming there exists a ![]() $G$-Kisin module
$G$-Kisin module ![]() $\overline {\mathfrak {P}}$ with coefficients in
$\overline {\mathfrak {P}}$ with coefficients in ![]() $\mathbf {F}$ with an isomorphism
$\mathbf {F}$ with an isomorphism ![]() $\overline {\gamma } : \widetilde {T}_{G,\mathbf {F}}(\overline {\mathfrak {P}}) \simeq {\overline {\rho }}|_{\Gamma _\infty }$. (This assumption is natural for our purposes as this is a necessary condition for
$\overline {\gamma } : \widetilde {T}_{G,\mathbf {F}}(\overline {\mathfrak {P}}) \simeq {\overline {\rho }}|_{\Gamma _\infty }$. (This assumption is natural for our purposes as this is a necessary condition for ![]() ${\overline {\rho }}$ to admit a crystalline lift.) Let
${\overline {\rho }}$ to admit a crystalline lift.) Let ![]() $D_{{\overline {\rho }}}^{\mu,\square }$ be the deformation functor associated to the deformation ring
$D_{{\overline {\rho }}}^{\mu,\square }$ be the deformation functor associated to the deformation ring ![]() $R_{\overline {\rho }}^{\mu,\square }$ for crystalline representations of
$R_{\overline {\rho }}^{\mu,\square }$ for crystalline representations of ![]() $p$-adic Hodge type
$p$-adic Hodge type ![]() $\mu$ from Fact 2.4.2.
$\mu$ from Fact 2.4.2.
Definition 3.3.2 For fixed ![]() ${\overline {\rho }}$,
${\overline {\rho }}$, ![]() $\overline {\mathfrak {P}}$, and
$\overline {\mathfrak {P}}$, and ![]() $\overline {\gamma }$, we define the following deformation problems on
$\overline {\gamma }$, we define the following deformation problems on ![]() $\mathcal {C}_{\Lambda }$:
$\mathcal {C}_{\Lambda }$:
(i) define
 $D_{{\overline {\rho }}, \overline {\mathfrak {P}}}^{\mu,\square }$ by
where
$D_{{\overline {\rho }}, \overline {\mathfrak {P}}}^{\mu,\square }$ by
where \[ D_{{\overline{\rho}}, \overline{\mathfrak{P}}}^{\mu,\square} (A) = \Big\{\!(\mathfrak{P}, \rho, \delta)\, | \, \mathfrak{P} \in D_{\overline{\mathfrak{P}}}^{\leqslant \mu}(A), \, \rho \in D^{\mu,\square}_{{\overline{\rho}}}(A), \, \rho|_{\Gamma_{\infty}} \overset{\delta} \simeq \widetilde{T}_{G,A}(\mathfrak{P})\!\Big\} \]
\[ D_{{\overline{\rho}}, \overline{\mathfrak{P}}}^{\mu,\square} (A) = \Big\{\!(\mathfrak{P}, \rho, \delta)\, | \, \mathfrak{P} \in D_{\overline{\mathfrak{P}}}^{\leqslant \mu}(A), \, \rho \in D^{\mu,\square}_{{\overline{\rho}}}(A), \, \rho|_{\Gamma_{\infty}} \overset{\delta} \simeq \widetilde{T}_{G,A}(\mathfrak{P})\!\Big\} \]
 $\delta$ lifts
$\delta$ lifts  $\overline {\gamma }$;
$\overline {\gamma }$;(ii) define
 $D_{{\overline {\rho }}, \overline {\mathfrak {P}}}^{\mu,\beta, \square }$ by
where
$D_{{\overline {\rho }}, \overline {\mathfrak {P}}}^{\mu,\beta, \square }$ by
where \[ d_{{\overline{\rho}}, \overline{\mathfrak{P}}}^{\mu,\beta,\square} (A) = \Big \{\!(\mathfrak{P}, \rho, \delta,\beta)\, | \, (\mathfrak{P},\rho,\delta) \in D_{{\overline{\rho}}, \overline{\mathfrak{P}}}^{\mu,\square}(A), \, (\mathfrak{P},\beta) \in D_{\overline{\mathfrak{P}}}^{\leqslant \mu, \beta} (A)\!\Big\} \]
\[ d_{{\overline{\rho}}, \overline{\mathfrak{P}}}^{\mu,\beta,\square} (A) = \Big \{\!(\mathfrak{P}, \rho, \delta,\beta)\, | \, (\mathfrak{P},\rho,\delta) \in D_{{\overline{\rho}}, \overline{\mathfrak{P}}}^{\mu,\square}(A), \, (\mathfrak{P},\beta) \in D_{\overline{\mathfrak{P}}}^{\leqslant \mu, \beta} (A)\!\Big\} \]
 $\beta$ lifts
$\beta$ lifts  $\overline {\beta }$;
$\overline {\beta }$;(iii) define
 $D_{\overline {\mathfrak {P}}}^{\leqslant \mu,\beta,\square }$ by
$D_{\overline {\mathfrak {P}}}^{\leqslant \mu,\beta,\square }$ by
 \[ D_{\overline{\mathfrak{P}}}^{\leqslant \mu,\beta,\square}(A) = \Big \{\!(\mathfrak{P}, \beta , \alpha ) : (\mathfrak{P}, \beta) \in D_{\overline{\mathfrak{P}}}^{\leqslant \mu,\beta}(A),\, \alpha \text{ trivializes } \widetilde{T}_{G,A}(\mathfrak{P})\!\Big\}. \]
\[ D_{\overline{\mathfrak{P}}}^{\leqslant \mu,\beta,\square}(A) = \Big \{\!(\mathfrak{P}, \beta , \alpha ) : (\mathfrak{P}, \beta) \in D_{\overline{\mathfrak{P}}}^{\leqslant \mu,\beta}(A),\, \alpha \text{ trivializes } \widetilde{T}_{G,A}(\mathfrak{P})\!\Big\}. \]
There are natural forgetful maps between these deformation problems:

Remark 3.3.3 If ![]() $A$ is the ring of integers in a finite extension of
$A$ is the ring of integers in a finite extension of ![]() $\Lambda$, or if
$\Lambda$, or if ![]() $A$ is a
$A$ is a ![]() $L$-algebra, then the Galois representation
$L$-algebra, then the Galois representation ![]() $\rho$ in the above definitions has
$\rho$ in the above definitions has ![]() $p$-adic Hodge type
$p$-adic Hodge type ![]() $\mu$. However, in general (for example, if
$\mu$. However, in general (for example, if ![]() $A$ is torsion), we cannot speak of the Galois representation or the
$A$ is torsion), we cannot speak of the Galois representation or the ![]() $G$-Kisin module having type
$G$-Kisin module having type ![]() $\mu$. We can only require that the
$\mu$. We can only require that the ![]() $G$-Kisin module have type
$G$-Kisin module have type ![]() $\leqslant \mu$ or that the Galois representation be an
$\leqslant \mu$ or that the Galois representation be an ![]() $A$-point of
$A$-point of ![]() $R^{\mu,\square }_{{\overline {\rho }}}$. We reiterate that we require
$R^{\mu,\square }_{{\overline {\rho }}}$. We reiterate that we require ![]() $p \nmid \# \pi _1(G^{\operatorname {der}})$ in order to use Theorem 2.3.1 to define
$p \nmid \# \pi _1(G^{\operatorname {der}})$ in order to use Theorem 2.3.1 to define ![]() $Y^{\leqslant \mu }$ and study
$Y^{\leqslant \mu }$ and study ![]() $G$-Kisin modules of type
$G$-Kisin modules of type ![]() $\leqslant \mu$.
$\leqslant \mu$.
Because of the presence of framings or trivializations, these deformation problems are easily seen to be pro-representable by complete local Noetherian rings which we denote by ![]() $R_{{\overline {\rho }}, \overline {\mathfrak {P}}}^{\mu,\square }$, by
$R_{{\overline {\rho }}, \overline {\mathfrak {P}}}^{\mu,\square }$, by ![]() $R_{{\overline {\rho }}, \overline {\mathfrak {P}}}^{\mu,\beta,\square }$, and by
$R_{{\overline {\rho }}, \overline {\mathfrak {P}}}^{\mu,\beta,\square }$, and by ![]() $R_{\overline {\mathfrak {P}}}^{\leqslant \mu,\beta,\square }$, respectively.
$R_{\overline {\mathfrak {P}}}^{\leqslant \mu,\beta,\square }$, respectively.
Lemma 3.3.4 The rings ![]() $R^{\leqslant \mu, \beta }_{\overline {\mathfrak {P}}}$ and
$R^{\leqslant \mu, \beta }_{\overline {\mathfrak {P}}}$ and ![]() $R^{\leqslant \mu, \beta, \square }_{\overline {\mathfrak {P}}}$ are
$R^{\leqslant \mu, \beta, \square }_{\overline {\mathfrak {P}}}$ are ![]() $\Lambda$-flat with reduced generic fiber.
$\Lambda$-flat with reduced generic fiber.
Proof. This follows from [Reference LevinLev15, Proposition 3.3.6], the local model diagram [Reference LevinLev15, (3-3-9-2)], and Theorem 2.3.1.
In contrast, it is not clear that ![]() $R_{{\overline {\rho }}, \overline {\mathfrak {P}}}^{\mu,\square }$ and
$R_{{\overline {\rho }}, \overline {\mathfrak {P}}}^{\mu,\square }$ and ![]() $R_{{\overline {\rho }}, \overline {\mathfrak {P}}}^{\mu,\beta,\square }$ are
$R_{{\overline {\rho }}, \overline {\mathfrak {P}}}^{\mu,\beta,\square }$ are ![]() $\Lambda$-flat.
$\Lambda$-flat.
Definition 3.3.5 Define ![]() $R_{{\overline {\rho }}, \overline {\mathfrak {P}}}^{\mu,\square,\operatorname {flat}}$ (respectively,
$R_{{\overline {\rho }}, \overline {\mathfrak {P}}}^{\mu,\square,\operatorname {flat}}$ (respectively, ![]() $R_{{\overline {\rho }}, \overline {\mathfrak {P}}}^{\mu,\beta,\square,\operatorname {flat}}$) to be the flat closure of
$R_{{\overline {\rho }}, \overline {\mathfrak {P}}}^{\mu,\beta,\square,\operatorname {flat}}$) to be the flat closure of ![]() $R_{{\overline {\rho }}, \overline {\mathfrak {P}}}^{\mu,\square }$ (respectively,
$R_{{\overline {\rho }}, \overline {\mathfrak {P}}}^{\mu,\square }$ (respectively, ![]() $R_{{\overline {\rho }}, \overline {\mathfrak {P}}}^{\mu,\beta,\square }$).
$R_{{\overline {\rho }}, \overline {\mathfrak {P}}}^{\mu,\beta,\square }$).
We also analyze ![]() $D^{\leqslant \mu, \beta }_{\overline {\mathfrak {P}}}$ a bit more in characteristic
$D^{\leqslant \mu, \beta }_{\overline {\mathfrak {P}}}$ a bit more in characteristic ![]() $p$. We work over
$p$. We work over ![]() $\mathbf {F}$-algebras, where
$\mathbf {F}$-algebras, where ![]() $E(u)^n = u^n$. Define
$E(u)^n = u^n$. Define ![]() $G'_{(n)} := \operatorname {Res}_{(\mathfrak {S}_{\mathbf {F}}/u^n)/ \mathbf {F}} G_{\mathbf {F}}$, which is a smooth affine group scheme as it is the Weil restriction of
$G'_{(n)} := \operatorname {Res}_{(\mathfrak {S}_{\mathbf {F}}/u^n)/ \mathbf {F}} G_{\mathbf {F}}$, which is a smooth affine group scheme as it is the Weil restriction of ![]() $G_{\mathbf {F}}$ along the finite flat map
$G_{\mathbf {F}}$ along the finite flat map ![]() $(k[u]/u^n \otimes _{\mathbf {F}_p} \mathbf {F})/\mathbf {F}$. There is a natural map
$(k[u]/u^n \otimes _{\mathbf {F}_p} \mathbf {F})/\mathbf {F}$. There is a natural map ![]() $\textrm {L}^+G'_{\mathbf {F}} \rightarrow G'_{(n)}$ given by reduction mod
$\textrm {L}^+G'_{\mathbf {F}} \rightarrow G'_{(n)}$ given by reduction mod ![]() $u^n$. Define a group scheme
$u^n$. Define a group scheme ![]() $L^{+, (n)} G'_{\mathbf {F}}$ over
$L^{+, (n)} G'_{\mathbf {F}}$ over ![]() $\mathbf {F}$ to sit in the exact sequence
$\mathbf {F}$ to sit in the exact sequence
The following lemma says that the ![]() $\varphi$-conjugation action of
$\varphi$-conjugation action of ![]() $L^{+, (N)} G'$ can be ‘straightened’, where
$L^{+, (N)} G'$ can be ‘straightened’, where ![]() $N$ is a previously fixed integer satisfying
$N$ is a previously fixed integer satisfying ![]() $N > ({b-a})/({p-1})$.
$N > ({b-a})/({p-1})$.
Lemma 3.3.6 Let ![]() $A$ be an
$A$ be an ![]() $\mathbf {F}$-algebra, and consider
$\mathbf {F}$-algebra, and consider ![]() $C_1, C_2 \in G(\mathfrak {S}_A)$ such that
$C_1, C_2 \in G(\mathfrak {S}_A)$ such that ![]() $\rho _0(C_2)$ has height in
$\rho _0(C_2)$ has height in ![]() $[a,b]$. If
$[a,b]$. If ![]() $C_1 = g C_2$ for
$C_1 = g C_2$ for ![]() $g\in L^{+, (N)} G'_{\mathbf {F}}(A)$, then there exists
$g\in L^{+, (N)} G'_{\mathbf {F}}(A)$, then there exists ![]() $g' \in L^{+, (N)} G'_{\mathbf {F}}(A)$ such that
$g' \in L^{+, (N)} G'_{\mathbf {F}}(A)$ such that ![]() $C_1 = g' C_2 \varphi (g')^{-1}$.
$C_1 = g' C_2 \varphi (g')^{-1}$.
Proof. We are trying to solve the equation
This can be solved by the usual successive approximation argument taking ![]() $g_0' = g$ and defining
$g_0' = g$ and defining ![]() $g'_i = g C_2 \varphi (g'_{i-1}) C_2^{-1}$. Using that if
$g'_i = g C_2 \varphi (g'_{i-1}) C_2^{-1}$. Using that if ![]() $g'_{i-1} \in L^{+, (n)} G'_{\mathbf {F}}(A)$ for
$g'_{i-1} \in L^{+, (n)} G'_{\mathbf {F}}(A)$ for ![]() $n \geqslant N$, then
$n \geqslant N$, then ![]() $C_2 \varphi (g'_{i-1}) C_2^{-1} \in L^{+, (n+1)} G'_{\mathbf {F}}(A)$, the
$C_2 \varphi (g'_{i-1}) C_2^{-1} \in L^{+, (n+1)} G'_{\mathbf {F}}(A)$, the ![]() $g'_i$ converge
$g'_i$ converge ![]() $u$-adically to the desired element
$u$-adically to the desired element ![]() $g'$.
$g'$.
Proposition 3.3.7 Assume ![]() $\overline {\mathfrak {P}}$ has type
$\overline {\mathfrak {P}}$ has type ![]() $\leqslant \mu$ and so
$\leqslant \mu$ and so ![]() $x =\Psi (\overline {\mathfrak {P}}, \overline {\beta }) \in \operatorname {Gr}^{\leqslant \mu }_{G'_{\mathbf {F}}}(\mathbf {F})$. Then
$x =\Psi (\overline {\mathfrak {P}}, \overline {\beta }) \in \operatorname {Gr}^{\leqslant \mu }_{G'_{\mathbf {F}}}(\mathbf {F})$. Then ![]() $\Psi$ induces a formally smooth morphism
$\Psi$ induces a formally smooth morphism
of relative dimension ![]() $\dim G'_{(N)}$.
$\dim G'_{(N)}$.
Proof. Let ![]() $A \in \mathcal {C}_{\Lambda }$ be killed by
$A \in \mathcal {C}_{\Lambda }$ be killed by ![]() $p$ and let
$p$ and let ![]() $I$ be a nilpotent ideal. Given
$I$ be a nilpotent ideal. Given ![]() $(\mathfrak {P}_{A/I}, \beta _{A/I}) \in D^{\leqslant \mu, \beta }_{\overline {\mathfrak {P}}}(A/I)$, choose a trivialization
$(\mathfrak {P}_{A/I}, \beta _{A/I}) \in D^{\leqslant \mu, \beta }_{\overline {\mathfrak {P}}}(A/I)$, choose a trivialization ![]() $\widetilde {\beta }_{A/I}$ of
$\widetilde {\beta }_{A/I}$ of ![]() $\mathfrak {P}_{A/I}$ over
$\mathfrak {P}_{A/I}$ over ![]() $\mathfrak {S}_{A/I}$ lifting
$\mathfrak {S}_{A/I}$ lifting ![]() $\beta _{A/I}$. The Frobenius trivializes to an element
$\beta _{A/I}$. The Frobenius trivializes to an element ![]() $C_{A/I} \in G(\mathfrak {S}_{A/I}[1/u])$. Note that
$C_{A/I} \in G(\mathfrak {S}_{A/I}[1/u])$. Note that ![]() $\Psi (\mathfrak {P}_{A/I}, \beta _{A/I}) = x = [C_{A/I}]$ in
$\Psi (\mathfrak {P}_{A/I}, \beta _{A/I}) = x = [C_{A/I}]$ in ![]() $\operatorname {Gr}_{G'_{\mathbf {F}}}(A/I)$.
$\operatorname {Gr}_{G'_{\mathbf {F}}}(A/I)$.
Assume we have a point ![]() $\widetilde {x} \in \operatorname {Gr}^{\leqslant \mu }_{G'_{\mathbf {F}}}(A)$ lifting
$\widetilde {x} \in \operatorname {Gr}^{\leqslant \mu }_{G'_{\mathbf {F}}}(A)$ lifting ![]() $x=[C_{A/I}]$. Since
$x=[C_{A/I}]$. Since ![]() $\textrm {L}^+G'$ is formally smooth as functor on
$\textrm {L}^+G'$ is formally smooth as functor on ![]() $\Lambda$-algebras, we can choose a representative
$\Lambda$-algebras, we can choose a representative ![]() $C_A$ for the class
$C_A$ for the class ![]() $\widetilde {x}$ such that
$\widetilde {x}$ such that ![]() $C_A\!\! \mod I = C_{A/I}$. We can construct a
$C_A\!\! \mod I = C_{A/I}$. We can construct a ![]() $G$-Kisin module
$G$-Kisin module ![]() $\mathfrak {P}_A$ with coefficients in
$\mathfrak {P}_A$ with coefficients in ![]() $A$ lifting
$A$ lifting ![]() $\mathfrak {P}_{A/I}$ equipped with a trivialization
$\mathfrak {P}_{A/I}$ equipped with a trivialization ![]() $\widetilde {\beta }_A$ lifting
$\widetilde {\beta }_A$ lifting ![]() $\widetilde {\beta }_{A/I}$ and with Frobenius given by
$\widetilde {\beta }_{A/I}$ and with Frobenius given by ![]() $C_A$. If we take
$C_A$. If we take ![]() $\beta _A = \widetilde {\beta }_A \!\!\mod E(u)^N$, it is clear that
$\beta _A = \widetilde {\beta }_A \!\!\mod E(u)^N$, it is clear that ![]() $(\mathfrak {P}_A, \beta _A)$ deforms
$(\mathfrak {P}_A, \beta _A)$ deforms ![]() $(\mathfrak {P}_{A/I}, \beta _{A/I})$ and it has type
$(\mathfrak {P}_{A/I}, \beta _{A/I})$ and it has type ![]() $\leqslant \mu$ since
$\leqslant \mu$ since ![]() $\widetilde {x} \in \operatorname {Gr}^{\leqslant \mu }_{G'_{\mathbf {F}}}(A)$.
$\widetilde {x} \in \operatorname {Gr}^{\leqslant \mu }_{G'_{\mathbf {F}}}(A)$.
The fiber of ![]() $\Psi ^{\mu }_{\mathbf {F}}$ over
$\Psi ^{\mu }_{\mathbf {F}}$ over ![]() $[C_A]$ can be identified with
$[C_A]$ can be identified with
where the action is by ![]() $\varphi$-conjugation and the subscript
$\varphi$-conjugation and the subscript ![]() $e$ indicates that we require elements to be the identity modulo the maximal ideal of
$e$ indicates that we require elements to be the identity modulo the maximal ideal of ![]() $A$. By Lemma 3.3.6, we have
$A$. By Lemma 3.3.6, we have
and, hence, the fiber is a torsor for ![]() $(G'_{(N)}(A))_e$. This proves the dimension formula.
$(G'_{(N)}(A))_e$. This proves the dimension formula.
Finally, we recall a resolution of ![]() $\operatorname {Spec} R^{\mu, \square }_{\overline {\rho }}$ introduced by Kisin for
$\operatorname {Spec} R^{\mu, \square }_{\overline {\rho }}$ introduced by Kisin for ![]() $\operatorname {GL}_n$ and constructed in [Reference LevinLev15] for
$\operatorname {GL}_n$ and constructed in [Reference LevinLev15] for ![]() $G$-valued representations.
$G$-valued representations.
Proposition 3.3.8 The Kisin resolution ![]() $X^{\mu }_{{\overline {\rho }}}$ is a projective
$X^{\mu }_{{\overline {\rho }}}$ is a projective ![]() $R^{\mu, \square }_{{\overline {\rho }}}$-scheme
$R^{\mu, \square }_{{\overline {\rho }}}$-scheme ![]() $($flat over
$($flat over ![]() $\Lambda )$ such that the following hold.
$\Lambda )$ such that the following hold.
(i) For any
 $x \in X^{\mu }_{{\overline {\rho }}}(\mathbf {F}')$, let
$x \in X^{\mu }_{{\overline {\rho }}}(\mathbf {F}')$, let  $\widehat {\mathcal {O}}_x^{\mu }$ denote the complete local ring of
$\widehat {\mathcal {O}}_x^{\mu }$ denote the complete local ring of  $X^{\mu }_{{\overline {\rho }}}$ at
$X^{\mu }_{{\overline {\rho }}}$ at  $x$. There is a corresponding
$x$. There is a corresponding  $G$-Kisin lattice
$G$-Kisin lattice  $\mathfrak {P}$ and a closed immersion
which is an isomorphism modulo
$\mathfrak {P}$ and a closed immersion
which is an isomorphism modulo \[ \operatorname{Spf} \widehat{\mathcal{O}}_x^{\mu} \rightarrow D_{{\overline{\rho}}_{\mathbf{F}'}, \mathfrak{P}}^{\mu,\square} \]
\[ \operatorname{Spf} \widehat{\mathcal{O}}_x^{\mu} \rightarrow D_{{\overline{\rho}}_{\mathbf{F}'}, \mathfrak{P}}^{\mu,\square} \]
 $p$-power torsion.
$p$-power torsion.(ii) Let
 $\mathfrak {m}$ denote maximal ideal of
$\mathfrak {m}$ denote maximal ideal of  $R^{\mu, \square }_{{\overline {\rho }}}$, let
$R^{\mu, \square }_{{\overline {\rho }}}$, let  $\rho$ denote the universal deformation, and let
$\rho$ denote the universal deformation, and let  $X^{\mu }_{{\overline {\rho }}, \mathfrak {m}}$ denote the fiber over the closed point of
$X^{\mu }_{{\overline {\rho }}, \mathfrak {m}}$ denote the fiber over the closed point of  $\operatorname {Spec} R^{\mu,\square }_{\overline {\rho }}$. For any Artinian local
$\operatorname {Spec} R^{\mu,\square }_{\overline {\rho }}$. For any Artinian local  $\mathbf {F}$-algebra
$\mathbf {F}$-algebra  $A$,
$A$,
 \[ X^{\mu}_{{\overline{\rho}}, \mathfrak{m}}(A) \subset \{ \mathfrak{P} \mid \mathfrak{P} \text{ is a }G\text{-Kisin lattice in } M_{G,\mathbf{F}}(\rho|_{\Gamma_\infty}) \otimes_{\mathcal{O}_{\mathcal{E}, \mathbf{F}}} \mathcal{O}_{\mathcal{E}, A} \text{ with type } \leqslant \mu \}. \]
\[ X^{\mu}_{{\overline{\rho}}, \mathfrak{m}}(A) \subset \{ \mathfrak{P} \mid \mathfrak{P} \text{ is a }G\text{-Kisin lattice in } M_{G,\mathbf{F}}(\rho|_{\Gamma_\infty}) \otimes_{\mathcal{O}_{\mathcal{E}, \mathbf{F}}} \mathcal{O}_{\mathcal{E}, A} \text{ with type } \leqslant \mu \}. \]
(iii) If
 $\Theta :X^{\mu }_{{\overline {\rho }}} \rightarrow \operatorname {Spec} R^{\mu, \square }_{{\overline {\rho }}}$ is the structure map, then
$\Theta :X^{\mu }_{{\overline {\rho }}} \rightarrow \operatorname {Spec} R^{\mu, \square }_{{\overline {\rho }}}$ is the structure map, then  $\Theta [ {1}/{p}]$ is an isomorphism.
$\Theta [ {1}/{p}]$ is an isomorphism.
Proof. Parts (i) and (iii) follow from Corollary 3.3.15 of [Reference LevinLev15], and part (ii) is an immediate consequence of part (i). The only difference with [Reference LevinLev15] is rather than all weights ![]() $\leqslant \mu$, we restrict to those with exactly weight
$\leqslant \mu$, we restrict to those with exactly weight ![]() $\mu$. In particular,
$\mu$. In particular, ![]() $X^{\mu }_{{\overline {\rho }}}$ is the closure of
$X^{\mu }_{{\overline {\rho }}}$ is the closure of ![]() $\operatorname {Spec} R^{\mu, \square }_{{\overline {\rho }}}[1/p]$ in
$\operatorname {Spec} R^{\mu, \square }_{{\overline {\rho }}}[1/p]$ in ![]() $X^{\mathrm {cris}, \leqslant \mu }_{{\overline {\rho }}}$ (see Definition 3.3.14 in [Reference LevinLev15]).
$X^{\mathrm {cris}, \leqslant \mu }_{{\overline {\rho }}}$ (see Definition 3.3.14 in [Reference LevinLev15]).
4. The monodromy condition
As before, we let ![]() $\Lambda$ be the ring of integers in a
$\Lambda$ be the ring of integers in a ![]() $p$-adic field
$p$-adic field ![]() $L$ with residue field
$L$ with residue field ![]() $\mathbf {F}$, and
$\mathbf {F}$, and ![]() $G$ be a split reductive group defined over
$G$ be a split reductive group defined over ![]() $\Lambda$. We continue to fix a
$\Lambda$. We continue to fix a ![]() $p$-adic field
$p$-adic field ![]() $K$ unramified over
$K$ unramified over ![]() $\mathbf {Q}_p$ with residue field
$\mathbf {Q}_p$ with residue field ![]() $k$ and ring of integers
$k$ and ring of integers ![]() $W(k)$. Throughout this section, we assume that
$W(k)$. Throughout this section, we assume that ![]() $p \nmid \# \pi _1(G^{\operatorname {der}})$.
$p \nmid \# \pi _1(G^{\operatorname {der}})$.
In this section, we study the difference between ![]() $\operatorname {Spf} R_{\overline {\mathfrak {P}},{\overline {\rho }}}^{\leqslant \mu,\beta,\square }$ and
$\operatorname {Spf} R_{\overline {\mathfrak {P}},{\overline {\rho }}}^{\leqslant \mu,\beta,\square }$ and ![]() $\operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu,\beta,\square }$. The difficulty is identifying which Kisin modules give rise to crystalline representations as opposed to just
$\operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu,\beta,\square }$. The difficulty is identifying which Kisin modules give rise to crystalline representations as opposed to just ![]() $\Gamma _{\infty }$-representations. To prove our main theorem, it suffices to obtain a bound on the special fiber. This is accomplished by a monodromy condition introduced in [Reference KisinKis09], which we recall and adapt to
$\Gamma _{\infty }$-representations. To prove our main theorem, it suffices to obtain a bound on the special fiber. This is accomplished by a monodromy condition introduced in [Reference KisinKis09], which we recall and adapt to ![]() $G$-Kisin modules in § 4.1. In § 4.2, we follow the strategy introduced in [Reference Le, Le Hung, Levin and MorraLLHLM18] to find a
$G$-Kisin modules in § 4.1. In § 4.2, we follow the strategy introduced in [Reference Le, Le Hung, Levin and MorraLLHLM18] to find a ![]() $p$-adic approximation for the monodromy condition and understand its reduction modulo
$p$-adic approximation for the monodromy condition and understand its reduction modulo ![]() $p$.
$p$.
4.1 The monodromy condition
Let ![]() $\mathcal {O}^{\operatorname {rig}}$ denote the ring of rigid analytic functions on the open unit disc over
$\mathcal {O}^{\operatorname {rig}}$ denote the ring of rigid analytic functions on the open unit disc over ![]() $K$, and fix an embedding
$K$, and fix an embedding ![]() $\mathcal {O}^{\operatorname {rig}} \hookrightarrow K[\![u ] \!]$. Note that
$\mathcal {O}^{\operatorname {rig}} \hookrightarrow K[\![u ] \!]$. Note that ![]() $\mathfrak {S}[1/p]$ is identified with the subring of bounded functions on that disc, that
$\mathfrak {S}[1/p]$ is identified with the subring of bounded functions on that disc, that ![]() $\mathcal {O}^{\operatorname {rig}}$ consists of power series
$\mathcal {O}^{\operatorname {rig}}$ consists of power series ![]() $\sum a_n u^n$ such that
$\sum a_n u^n$ such that ![]() $\lim _{n \to \infty } |a_n |_p r^n = 0$ for any
$\lim _{n \to \infty } |a_n |_p r^n = 0$ for any ![]() $r<1$, and that the Frobenius of
$r<1$, and that the Frobenius of ![]() $\mathfrak {S}$ extends to
$\mathfrak {S}$ extends to ![]() $\mathcal {O}^{\operatorname {rig}}$. For a Kisin module
$\mathcal {O}^{\operatorname {rig}}$. For a Kisin module ![]() $\mathfrak {M}$ with coefficients in a finite flat
$\mathfrak {M}$ with coefficients in a finite flat ![]() $\Lambda$-algebra
$\Lambda$-algebra ![]() $A$, we define
$A$, we define ![]() $\mathcal {O}^{\operatorname {rig}}_A := \mathcal {O}^{\operatorname {rig}} \otimes _{\mathbf {Z}_p} A$ and
$\mathcal {O}^{\operatorname {rig}}_A := \mathcal {O}^{\operatorname {rig}} \otimes _{\mathbf {Z}_p} A$ and ![]() $\mathfrak {M}^{\operatorname {rig}} := \mathfrak {M} \otimes _{\mathfrak {S}} \mathcal {O}^{\operatorname {rig}}$. For a
$\mathfrak {M}^{\operatorname {rig}} := \mathfrak {M} \otimes _{\mathfrak {S}} \mathcal {O}^{\operatorname {rig}}$. For a ![]() $G$-Kisin module
$G$-Kisin module ![]() $\mathfrak {P}$ with coefficients in
$\mathfrak {P}$ with coefficients in ![]() $A$, we define
$A$, we define ![]() $\mathfrak {P}^{\operatorname {rig}} := \mathfrak {P} \times _{\operatorname {Spec} \mathfrak {S}} \operatorname {Spec}(\mathcal {O}^{{\operatorname {rig}}})$.
$\mathfrak {P}^{\operatorname {rig}} := \mathfrak {P} \times _{\operatorname {Spec} \mathfrak {S}} \operatorname {Spec}(\mathcal {O}^{{\operatorname {rig}}})$.
Define ![]() $\lambda \in \mathcal {O}^{\operatorname {rig}}$ by
$\lambda \in \mathcal {O}^{\operatorname {rig}}$ by
 \begin{align} \lambda :=
\prod_{n=0}^\infty \varphi^n \bigg( \frac{E(u)}{-p} \bigg)
= \prod_{n=0}^\infty \varphi^n \bigg( 1- \frac{u}{p}
\bigg). \end{align}
\begin{align} \lambda :=
\prod_{n=0}^\infty \varphi^n \bigg( \frac{E(u)}{-p} \bigg)
= \prod_{n=0}^\infty \varphi^n \bigg( 1- \frac{u}{p}
\bigg). \end{align}
We define a derivation ![]() $N_\nabla$ on
$N_\nabla$ on ![]() $\mathcal {O}^{\operatorname {rig}}$ by
$\mathcal {O}^{\operatorname {rig}}$ by ![]() $N_{\nabla } = - u \lambda ({d}/{du})$.
$N_{\nabla } = - u \lambda ({d}/{du})$.
For a ![]() $\Lambda$-algebra
$\Lambda$-algebra ![]() $A$ equipped with a
$A$ equipped with a ![]() $\Lambda$-linear derivation
$\Lambda$-linear derivation ![]() $N_A$, remember that a derivation over
$N_A$, remember that a derivation over ![]() $N_A$ on an
$N_A$ on an ![]() $A$-module
$A$-module ![]() $M$ is a function
$M$ is a function ![]() $N_M : M \to M$ such that
$N_M : M \to M$ such that ![]() $N_M(v+w) = N_M(v) + N_M(w)$ and
$N_M(v+w) = N_M(v) + N_M(w)$ and ![]() $N_M(cv) = N_A(c) v + c N_M(v)$ for
$N_M(cv) = N_A(c) v + c N_M(v)$ for ![]() $v,w \in M$ and
$v,w \in M$ and ![]() $c \in A$.
$c \in A$.
Example 4.1.1 Let ![]() $M$ be a
$M$ be a ![]() $\Lambda$-module. There is a trivial derivation
$\Lambda$-module. There is a trivial derivation ![]() $N^{\operatorname {triv}}_M$ on
$N^{\operatorname {triv}}_M$ on ![]() $M \otimes _{\mathbf {Z}_p} \mathcal {O}^{\operatorname {rig}}$ over
$M \otimes _{\mathbf {Z}_p} \mathcal {O}^{\operatorname {rig}}$ over ![]() $N_{\nabla }$ given by
$N_{\nabla }$ given by ![]() $1 \otimes N_{\nabla }$.
$1 \otimes N_{\nabla }$.
Remark 4.1.2 Given a basis ![]() $\beta = \{v_1,\ldots, v_n\}$ for a finitely generated free
$\beta = \{v_1,\ldots, v_n\}$ for a finitely generated free ![]() $A$-module
$A$-module ![]() $M$, a derivation
$M$, a derivation ![]() $N_M$ on
$N_M$ on ![]() $M$ can be represented by a matrix
$M$ can be represented by a matrix ![]() $[N_M]_\beta$ whose
$[N_M]_\beta$ whose ![]() $i$th column is the coefficients of
$i$th column is the coefficients of ![]() $N_M(v_i)$ written in the basis
$N_M(v_i)$ written in the basis ![]() $\{v_1,\ldots, v_n\}$. For example, the matrix for
$\{v_1,\ldots, v_n\}$. For example, the matrix for ![]() $N^{\operatorname {triv}}_M$ is the zero matrix. If
$N^{\operatorname {triv}}_M$ is the zero matrix. If ![]() $[T]_\beta$ is the matrix for a homomorphism
$[T]_\beta$ is the matrix for a homomorphism ![]() $T : M \to M$, then
$T : M \to M$, then
Fact 4.1.3 Let ![]() $A$ be a finite flat
$A$ be a finite flat ![]() $\Lambda$-algebra
$\Lambda$-algebra ![]() $A$ and let
$A$ and let ![]() $\mathfrak {M}$ be a Kisin module of bounded height. There is a unique derivation
$\mathfrak {M}$ be a Kisin module of bounded height. There is a unique derivation ![]() $N_{\mathfrak {M}}$ on
$N_{\mathfrak {M}}$ on ![]() $\mathfrak {M}^{\operatorname {rig}} [1/\lambda ]$ over
$\mathfrak {M}^{\operatorname {rig}} [1/\lambda ]$ over ![]() $N_\nabla$ such that
$N_\nabla$ such that ![]() $N _{\mathfrak {M}} \equiv 0 \mod {u}$ and such that as endomorphisms of
$N _{\mathfrak {M}} \equiv 0 \mod {u}$ and such that as endomorphisms of ![]() $\mathfrak {M}^{\operatorname {rig}}[1/\lambda ]$ we have
$\mathfrak {M}^{\operatorname {rig}}[1/\lambda ]$ we have
The module ![]() $\mathfrak {M}^{\operatorname {rig}}$ is preserved by
$\mathfrak {M}^{\operatorname {rig}}$ is preserved by ![]() $N_{\mathfrak {M}}$ if and only if
$N_{\mathfrak {M}}$ if and only if ![]() $(\widetilde {T}_{\operatorname {GL}_n,A} (\mathfrak {M}))[1/p]$ is the restriction to
$(\widetilde {T}_{\operatorname {GL}_n,A} (\mathfrak {M}))[1/p]$ is the restriction to ![]() $\Gamma _\infty$ of a crystalline
$\Gamma _\infty$ of a crystalline ![]() $\Gamma _K$-representation.
$\Gamma _K$-representation.
Except for uniqueness, this is essentially [Reference KisinKis06, Lemma 1.3.10 and Corollary 1.3.15]. The argument for uniqueness is routine, and is spelled out in [Reference Bergdall and LevinBL22, Lemma 2.2.1]. The condition that ![]() $N_\mathfrak {M}$ preserves
$N_\mathfrak {M}$ preserves ![]() $\mathfrak {M}^{\operatorname {rig}}$ is often referred to as the monodromy condition.
$\mathfrak {M}^{\operatorname {rig}}$ is often referred to as the monodromy condition.
We now generalize this to apply to ![]() $G$-Kisin modules. We begin by defining a notion of derivations on
$G$-Kisin modules. We begin by defining a notion of derivations on ![]() $G$-bundles. Let
$G$-bundles. Let ![]() $B$ be a
$B$ be a ![]() $\Lambda$-algebra equipped with a
$\Lambda$-algebra equipped with a ![]() $\Lambda$-linear derivation
$\Lambda$-linear derivation ![]() $N_B$.
$N_B$.
Definition 4.1.4 Let ![]() $\mathfrak {P}$ be a
$\mathfrak {P}$ be a ![]() $G$-bundle over
$G$-bundle over ![]() $B$ corresponding to a fiber functor
$B$ corresponding to a fiber functor ![]() $\eta : {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G) \to \operatorname {Proj}_{B}$. A derivation on
$\eta : {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G) \to \operatorname {Proj}_{B}$. A derivation on ![]() $\mathfrak {P}$ over
$\mathfrak {P}$ over ![]() $N_B$ is the data, for every
$N_B$ is the data, for every ![]() $G \to \operatorname {GL}(V)$, of a derivation
$G \to \operatorname {GL}(V)$, of a derivation ![]() $N_V$ on
$N_V$ on ![]() $\eta (V)$ over
$\eta (V)$ over ![]() $N_B$ such that:
$N_B$ such that:
(i) for a short exact sequence
 $0 \to V_1 \to V \to V_2$, the operators
$0 \to V_1 \to V \to V_2$, the operators  $N_V$,
$N_V$,  $N_{V_1}$, and
$N_{V_1}$, and  $N_{V_2}$ are compatible;
$N_{V_2}$ are compatible;(ii)
 $N_{V_1 \otimes V_2} = 1 \otimes N_{V_2} + N_{V_1} \otimes 1$.
$N_{V_1 \otimes V_2} = 1 \otimes N_{V_2} + N_{V_1} \otimes 1$.
Lemma 4.1.5 Let ![]() $\mathfrak {P}$ be a
$\mathfrak {P}$ be a ![]() $G$-bundle over
$G$-bundle over ![]() $B$ corresponding to a fiber functor
$B$ corresponding to a fiber functor ![]() $\eta : {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G) \to \operatorname {Proj}_{B}$. The set of derivations on
$\eta : {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G) \to \operatorname {Proj}_{B}$. The set of derivations on ![]() $\mathfrak {P}$ over
$\mathfrak {P}$ over ![]() $N_B$ are a
$N_B$ are a ![]() $\operatorname {Lie} G$-torsor. Fixing a trivialization of
$\operatorname {Lie} G$-torsor. Fixing a trivialization of ![]() $\mathfrak {P}$, the torsor is trivialized by the derivation
$\mathfrak {P}$, the torsor is trivialized by the derivation ![]() $N^{{\operatorname {triv}}}$ given by
$N^{{\operatorname {triv}}}$ given by ![]() $N^{\operatorname {triv}}_V = 1 \otimes N_{\nabla }$ on
$N^{\operatorname {triv}}_V = 1 \otimes N_{\nabla }$ on ![]() $V \otimes _{\Lambda } B$ for each
$V \otimes _{\Lambda } B$ for each ![]() $V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$.
$V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$.
Proof. Let ![]() $N$ and
$N$ and ![]() $N'$ be derivations on
$N'$ be derivations on ![]() $\mathfrak {P}$, and
$\mathfrak {P}$, and ![]() $X \in \mathfrak {g}_{B}$. For representations
$X \in \mathfrak {g}_{B}$. For representations ![]() $V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$, there are associated
$V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$, there are associated ![]() $N_V, X_V : \eta (V) \to \eta (V)$ as in Definition 4.1.4 and Example 2.2.1(c). A straightforward computation shows that
$N_V, X_V : \eta (V) \to \eta (V)$ as in Definition 4.1.4 and Example 2.2.1(c). A straightforward computation shows that ![]() $N + X$ (defined for
$N + X$ (defined for ![]() $V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$ by
$V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$ by ![]() $N_V + X_V$) is a derivation, and that
$N_V + X_V$) is a derivation, and that ![]() $N - N'$ (defined for
$N - N'$ (defined for ![]() $V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$ by
$V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$ by ![]() $N_{V} - N'_{V}$) is an element of
$N_{V} - N'_{V}$) is an element of ![]() $\mathfrak {g}_{B}$ again using Example 2.2.1(c). This establishes the first statement. Yet another straightforward check shows that
$\mathfrak {g}_{B}$ again using Example 2.2.1(c). This establishes the first statement. Yet another straightforward check shows that ![]() $N^{\operatorname {triv}}$ is a derivation, establishing the second.
$N^{\operatorname {triv}}$ is a derivation, establishing the second.
Remark 4.1.6 When ![]() $G = \operatorname {GL}(V)$ for a free
$G = \operatorname {GL}(V)$ for a free ![]() $B$-module
$B$-module ![]() $V$ of rank
$V$ of rank ![]() $n$, after picking a basis for
$n$, after picking a basis for ![]() $V$ the Lie algebra
$V$ the Lie algebra ![]() $(\operatorname {Lie} G)_B$ is identified with
$(\operatorname {Lie} G)_B$ is identified with ![]() $\operatorname {Mat}_n(B)$. Unwinding definitions, the matrix associated to a derivation in Remark 4.1.2 agrees with the element of
$\operatorname {Mat}_n(B)$. Unwinding definitions, the matrix associated to a derivation in Remark 4.1.2 agrees with the element of ![]() $(\operatorname {Lie} G)_B$ obtained by trivializing the torsor of derivations by
$(\operatorname {Lie} G)_B$ obtained by trivializing the torsor of derivations by ![]() $N^{\operatorname {triv}}$.
$N^{\operatorname {triv}}$.
By working with each ![]() $V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$ individually, we may compose derivations with (semi-linear) automorphisms. Of course, the result is only a function
$V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$ individually, we may compose derivations with (semi-linear) automorphisms. Of course, the result is only a function ![]() $V_B \to V_B$, and will not necessarily be a derivation. We may likewise define multiplication by scalars and base change.
$V_B \to V_B$, and will not necessarily be a derivation. We may likewise define multiplication by scalars and base change.
Proposition 4.1.7 Let ![]() $\mathfrak {P}$ be a
$\mathfrak {P}$ be a ![]() $G$-Kisin module with coefficients in a finite flat
$G$-Kisin module with coefficients in a finite flat ![]() $\Lambda$-algebra
$\Lambda$-algebra ![]() $A$. There is a unique derivation
$A$. There is a unique derivation ![]() $N_{\mathfrak {P}}$ on
$N_{\mathfrak {P}}$ on ![]() $\mathfrak {P}^{\operatorname {rig}}[1/\lambda ]$ over
$\mathfrak {P}^{\operatorname {rig}}[1/\lambda ]$ over ![]() $N_\nabla$ such that
$N_\nabla$ such that ![]() $N_{\mathfrak {P}} \equiv 0 \pmod {u}$ and
$N_{\mathfrak {P}} \equiv 0 \pmod {u}$ and
Proof. By Example 3.1.4, each ![]() $V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$ induces a Kisin module
$V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$ induces a Kisin module ![]() $\mathfrak {P}(V)$. Using Fact 4.1.3, we obtain a unique derivation
$\mathfrak {P}(V)$. Using Fact 4.1.3, we obtain a unique derivation ![]() $N_{\mathfrak {P},V}$ compatible with
$N_{\mathfrak {P},V}$ compatible with ![]() $\phi _V$ in the sense it satisfies (4.1.2). Compatibility of the
$\phi _V$ in the sense it satisfies (4.1.2). Compatibility of the ![]() $N_{\mathfrak {P},V}$ with exact sequences and tensor products follows from uniqueness, so the
$N_{\mathfrak {P},V}$ with exact sequences and tensor products follows from uniqueness, so the ![]() $N_{\mathfrak {P},V}$ collectively define a necessarily unique derivation
$N_{\mathfrak {P},V}$ collectively define a necessarily unique derivation ![]() $N_{\mathfrak {P}}$ on
$N_{\mathfrak {P}}$ on ![]() $\mathfrak {P}^{\operatorname {rig}}[1/\lambda ]$ satisfying (4.1.3).
$\mathfrak {P}^{\operatorname {rig}}[1/\lambda ]$ satisfying (4.1.3).
Corollary 4.1.8 Let ![]() $\mathfrak {P}$ be a
$\mathfrak {P}$ be a ![]() $G$-Kisin module with coefficients in
$G$-Kisin module with coefficients in ![]() $A$ as in Proposition 4.1.7. Fix a trivialization of
$A$ as in Proposition 4.1.7. Fix a trivialization of ![]() $\mathfrak {P}$ and trivialize the torsor of derivations on
$\mathfrak {P}$ and trivialize the torsor of derivations on ![]() $\mathfrak {P}^{\operatorname {rig}}[1/\lambda ]$ by
$\mathfrak {P}^{\operatorname {rig}}[1/\lambda ]$ by ![]() $N^{\operatorname {triv}}_{\mathfrak {P}}$. Letting
$N^{\operatorname {triv}}_{\mathfrak {P}}$. Letting ![]() $\phi _{\mathfrak {P}}$ trivialize to
$\phi _{\mathfrak {P}}$ trivialize to ![]() $C \in G(\mathcal {O}^{\operatorname {rig}}_A [1/\lambda ])$ and
$C \in G(\mathcal {O}^{\operatorname {rig}}_A [1/\lambda ])$ and ![]() $E(u)\phi _{\mathfrak {P}} \varphi ^*( N^{\operatorname {triv}}_{\mathfrak {P}}) \phi _{\mathfrak {P}}^{-1}$ trivialize to
$E(u)\phi _{\mathfrak {P}} \varphi ^*( N^{\operatorname {triv}}_{\mathfrak {P}}) \phi _{\mathfrak {P}}^{-1}$ trivialize to ![]() $N_1 \in \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_A [1/\lambda ]}$, we have that
$N_1 \in \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_A [1/\lambda ]}$, we have that ![]() $N_\mathfrak {P}$ trivializes to an
$N_\mathfrak {P}$ trivializes to an ![]() $N_\infty \in \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_A [1/\lambda ]}$ such that
$N_\infty \in \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_A [1/\lambda ]}$ such that
Proof. It is straightforward to verify that ![]() $\phi _{\mathfrak {P}} \varphi ^*(N^{\operatorname {triv}}_{\mathfrak {P}}) \phi ^{-1}_{\mathfrak {P}}$ is a derivation on
$\phi _{\mathfrak {P}} \varphi ^*(N^{\operatorname {triv}}_{\mathfrak {P}}) \phi ^{-1}_{\mathfrak {P}}$ is a derivation on ![]() $\varphi ^*(\mathfrak {P}) ^{{\operatorname {rig}}}[1/\lambda ]$. We may rewrite (4.1.3) as
$\varphi ^*(\mathfrak {P}) ^{{\operatorname {rig}}}[1/\lambda ]$. We may rewrite (4.1.3) as
again with the equality interpreted as equality of functions on ![]() $V$ for each
$V$ for each ![]() $V \in {^f} \hspace {-2pt} \operatorname {Rep}_\lambda (G)$. The left-hand side is a derivation which trivializes to
$V \in {^f} \hspace {-2pt} \operatorname {Rep}_\lambda (G)$. The left-hand side is a derivation which trivializes to ![]() $N_\infty$. On the right-hand side,
$N_\infty$. On the right-hand side, ![]() $E(u) \phi _\mathfrak {P} \varphi ^*(N_\mathfrak {P}) \phi _{\mathfrak {P}}^{-1}$ trivializes to
$E(u) \phi _\mathfrak {P} \varphi ^*(N_\mathfrak {P}) \phi _{\mathfrak {P}}^{-1}$ trivializes to
 \begin{align*} E(u) \phi_\mathfrak{P} \varphi^*(N_\mathfrak{P}) \phi_{\mathfrak{P}}^{-1} - N_\mathfrak{P}^{\operatorname{triv}} &= E(u) \phi_\mathfrak{P} \varphi^*(N_\mathfrak{P}) \phi_{\mathfrak{P}}^{-1} - E(u) \phi_\mathfrak{P} \varphi^*(N_\mathfrak{P}^{\operatorname{triv}}) \phi_\mathfrak{P}^{-1}\\ & \quad + E(u) \phi_\mathfrak{P} \varphi^*(N_\mathfrak{P}^{\operatorname{triv}}) \phi_\mathfrak{P}^{-1} - N_\mathfrak{P}^{\operatorname{triv}}. \end{align*}
\begin{align*} E(u) \phi_\mathfrak{P} \varphi^*(N_\mathfrak{P}) \phi_{\mathfrak{P}}^{-1} - N_\mathfrak{P}^{\operatorname{triv}} &= E(u) \phi_\mathfrak{P} \varphi^*(N_\mathfrak{P}) \phi_{\mathfrak{P}}^{-1} - E(u) \phi_\mathfrak{P} \varphi^*(N_\mathfrak{P}^{\operatorname{triv}}) \phi_\mathfrak{P}^{-1}\\ & \quad + E(u) \phi_\mathfrak{P} \varphi^*(N_\mathfrak{P}^{\operatorname{triv}}) \phi_\mathfrak{P}^{-1} - N_\mathfrak{P}^{\operatorname{triv}}. \end{align*}
Using Example 2.2.1(c), the endomorphism ![]() $E(u) \phi _\mathfrak {P} \varphi ^*(N_\mathfrak {P}) \phi _{\mathfrak {P}}^{-1} - E(u) \phi _\mathfrak {P} \varphi ^*(N_\mathfrak {P}^{\operatorname {triv}}) \phi _\mathfrak {P}^{-1}$ corresponds to
$E(u) \phi _\mathfrak {P} \varphi ^*(N_\mathfrak {P}) \phi _{\mathfrak {P}}^{-1} - E(u) \phi _\mathfrak {P} \varphi ^*(N_\mathfrak {P}^{\operatorname {triv}}) \phi _\mathfrak {P}^{-1}$ corresponds to ![]() $E(u) \operatorname {Ad}_G(C) (\varphi (N_\infty )) \in \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_A [1/\lambda ]}$. By definition,
$E(u) \operatorname {Ad}_G(C) (\varphi (N_\infty )) \in \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_A [1/\lambda ]}$. By definition, ![]() $E(u) \phi _\mathfrak {P} N_\mathfrak {P}^{\operatorname {triv}} \phi _\mathfrak {P}^{-1} - N_\mathfrak {P}^{\operatorname {triv}}$ corresponds to
$E(u) \phi _\mathfrak {P} N_\mathfrak {P}^{\operatorname {triv}} \phi _\mathfrak {P}^{-1} - N_\mathfrak {P}^{\operatorname {triv}}$ corresponds to ![]() $N_1$.
$N_1$.
Proposition 4.1.9 Let ![]() $\mathfrak {P}$ be a
$\mathfrak {P}$ be a ![]() $G$-Kisin module with coefficients in a finite flat
$G$-Kisin module with coefficients in a finite flat ![]() $\Lambda$-algebra
$\Lambda$-algebra ![]() $A$, and
$A$, and ![]() $N_\mathfrak {P}$ be the derivation on
$N_\mathfrak {P}$ be the derivation on ![]() $\mathfrak {P}^{\operatorname {rig}}[1/\lambda ]$. Then
$\mathfrak {P}^{\operatorname {rig}}[1/\lambda ]$. Then ![]() $\widetilde {T}_{G,A}(\mathfrak {P})[1/p]$ is the restriction to
$\widetilde {T}_{G,A}(\mathfrak {P})[1/p]$ is the restriction to ![]() $\Gamma _\infty$ of a crystalline
$\Gamma _\infty$ of a crystalline ![]() $G$-valued representation of
$G$-valued representation of ![]() $\Gamma _K$ if and only if
$\Gamma _K$ if and only if ![]() $N_{\mathfrak {P},V}( V \otimes \mathcal {O}^{{\operatorname {rig}}}_A) \subset V \otimes \mathcal {O}^{{\operatorname {rig}}}_A$ for every
$N_{\mathfrak {P},V}( V \otimes \mathcal {O}^{{\operatorname {rig}}}_A) \subset V \otimes \mathcal {O}^{{\operatorname {rig}}}_A$ for every ![]() $V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$.
$V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$.
Proof. This follows from the second part of Fact 4.1.3 and the fact that a ![]() $G$-valued representation is crystalline if and only if the representation on
$G$-valued representation is crystalline if and only if the representation on ![]() $V$ is crystalline for every
$V$ is crystalline for every ![]() $V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$.
$V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$.
As usual, it suffices to check that ![]() $N_{\mathfrak {P},V} ( \mathfrak {P}_V) \subset \mathfrak {P}_V$ for a single faithful representation
$N_{\mathfrak {P},V} ( \mathfrak {P}_V) \subset \mathfrak {P}_V$ for a single faithful representation ![]() $V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$. It also suffices to check, using the equivalence of Example 2.2.1(c), that the
$V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$. It also suffices to check, using the equivalence of Example 2.2.1(c), that the ![]() $N_\infty \in \mathfrak {g}_{\mathcal {O}_A^{\operatorname {rig}}[1/\lambda ]}$ corresponding to
$N_\infty \in \mathfrak {g}_{\mathcal {O}_A^{\operatorname {rig}}[1/\lambda ]}$ corresponding to ![]() $N_\mathfrak {P}$ actually lies in
$N_\mathfrak {P}$ actually lies in ![]() $\mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_A}$.
$\mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_A}$.
Definition 4.1.10 Let ![]() $\mathfrak {P}$ be a
$\mathfrak {P}$ be a ![]() $G$-Kisin module with coefficients in a finite flat
$G$-Kisin module with coefficients in a finite flat ![]() $\Lambda$-algebra
$\Lambda$-algebra ![]() $A$. Let
$A$. Let ![]() $N_\mathfrak {P}$ be the natural derivation on
$N_\mathfrak {P}$ be the natural derivation on ![]() $\mathfrak {P}_{\mathcal {O}^{\operatorname {rig}}[1/\lambda ]}$ which trivializes to
$\mathfrak {P}_{\mathcal {O}^{\operatorname {rig}}[1/\lambda ]}$ which trivializes to ![]() $N_\infty \in \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_A[1/\lambda ]}$. We say
$N_\infty \in \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_A[1/\lambda ]}$. We say ![]() $\mathfrak {P}$ (or
$\mathfrak {P}$ (or ![]() $N_\infty$) satisfies the monodromy condition if
$N_\infty$) satisfies the monodromy condition if ![]() $N_\infty \in \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_A}$.
$N_\infty \in \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_A}$.
We immediately obtain the following result.
Corollary 4.1.11 With the notation of Proposition 4.1.9, ![]() $\widetilde {T}_{G,A}(\mathfrak {P})[1/p]$ is the restriction to
$\widetilde {T}_{G,A}(\mathfrak {P})[1/p]$ is the restriction to ![]() $\Gamma _\infty$ of a crystalline
$\Gamma _\infty$ of a crystalline ![]() $G$-valued representation of
$G$-valued representation of ![]() $\Gamma _K\!\!$ if and only if
$\Gamma _K\!\!$ if and only if ![]() $\mathfrak {P}$ satisfies the monodromy condition.
$\mathfrak {P}$ satisfies the monodromy condition.
Remark 4.1.12 When ![]() $G = \operatorname {GL}(V)$, after fixing a basis
$G = \operatorname {GL}(V)$, after fixing a basis ![]() $\beta$ for
$\beta$ for ![]() $V$ the trivial derivation corresponds to the zero matrix. Furthermore, we claim that the derivation
$V$ the trivial derivation corresponds to the zero matrix. Furthermore, we claim that the derivation ![]() $E(u) \phi _{\mathfrak {P}} \varphi ^*(N^{\operatorname {triv}}_{\mathfrak {P}}) \phi ^{-1}_{\mathfrak {P}}$ trivializes to
$E(u) \phi _{\mathfrak {P}} \varphi ^*(N^{\operatorname {triv}}_{\mathfrak {P}}) \phi ^{-1}_{\mathfrak {P}}$ trivializes to ![]() $N_{\nabla }(C) C^{-1} = - u \lambda ({dC}/{du}) C^{-1}$ where
$N_{\nabla }(C) C^{-1} = - u \lambda ({dC}/{du}) C^{-1}$ where ![]() $C = [\phi _\mathfrak {P}]_\beta$ is the matrix of
$C = [\phi _\mathfrak {P}]_\beta$ is the matrix of ![]() $\phi _\mathfrak {P}$ with respect to
$\phi _\mathfrak {P}$ with respect to ![]() $\beta$.
$\beta$.
Since ![]() $\phi _\mathfrak {P}$ is semi-linear, note that
$\phi _\mathfrak {P}$ is semi-linear, note that ![]() $C \varphi ([\phi _\mathfrak {P}^{-1}]_\beta ) = 1$, and since
$C \varphi ([\phi _\mathfrak {P}^{-1}]_\beta ) = 1$, and since ![]() $N_\nabla$ is a derivation note that
$N_\nabla$ is a derivation note that
Using that ![]() $-E(u) \varphi \circ N_\nabla = N_\nabla \circ \varphi$, which can be checked on power series, we compute that
$-E(u) \varphi \circ N_\nabla = N_\nabla \circ \varphi$, which can be checked on power series, we compute that
 \begin{align*} E(u) [\phi_{\mathfrak{P}} \varphi^*(N^{\operatorname{triv}}_{\mathfrak{P}}) \phi^{-1}_{\mathfrak{P}}]_\beta & = E(u) C \cdot \varphi \big( [N^{\operatorname{triv}}_{\mathfrak{P}}]_\beta [\phi^{-1}_{\mathfrak{P}}]_\beta + N_\nabla( [\phi^{-1}_{\mathfrak{P}}]_\beta ) \big)\\ & = E(u) C \varphi( N_\nabla( [\phi^{-1}_{\mathfrak{P}} ]_\beta )) = -C N_\nabla(\varphi([\phi_\mathfrak{P}^{-1}]_\beta)) \\ &= -C N_\nabla(C^{-1}) = N_\nabla(C) C^{-1}. \end{align*}
\begin{align*} E(u) [\phi_{\mathfrak{P}} \varphi^*(N^{\operatorname{triv}}_{\mathfrak{P}}) \phi^{-1}_{\mathfrak{P}}]_\beta & = E(u) C \cdot \varphi \big( [N^{\operatorname{triv}}_{\mathfrak{P}}]_\beta [\phi^{-1}_{\mathfrak{P}}]_\beta + N_\nabla( [\phi^{-1}_{\mathfrak{P}}]_\beta ) \big)\\ & = E(u) C \varphi( N_\nabla( [\phi^{-1}_{\mathfrak{P}} ]_\beta )) = -C N_\nabla(\varphi([\phi_\mathfrak{P}^{-1}]_\beta)) \\ &= -C N_\nabla(C^{-1}) = N_\nabla(C) C^{-1}. \end{align*}
This gives the claim, and also an explicit description of ![]() $N_1$. Using this, (4.1.4) is equivalent to
$N_1$. Using this, (4.1.4) is equivalent to
For general ![]() $G$, if we trivialize
$G$, if we trivialize ![]() $\mathfrak {P}$, and hence for every
$\mathfrak {P}$, and hence for every ![]() $V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$ obtain a basis for
$V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$ obtain a basis for ![]() $V$, we obtain a derivation and semi-linear automorphism of
$V$, we obtain a derivation and semi-linear automorphism of ![]() $V$. These are represented by matrices
$V$. These are represented by matrices ![]() $N_{\infty,V}$ and
$N_{\infty,V}$ and ![]() $C_V$ such that
$C_V$ such that
We see that ![]() $N_{1,V} = - u \lambda ({d C_V}/{du}) C_V^{-1}$.
$N_{1,V} = - u \lambda ({d C_V}/{du}) C_V^{-1}$.
In light of Remark 4.1.12, we introduce some convenient notation for later.
Definition 4.1.13 For any ![]() $\Lambda$-algebra
$\Lambda$-algebra ![]() $A$ and
$A$ and ![]() $C \in \operatorname {LG}'(A)$, let
$C \in \operatorname {LG}'(A)$, let ![]() $ ({dC}/{du}) C^{-1} \in \operatorname {Lie} \operatorname {LG}'(A)$ correspond to the endomorphism given by
$ ({dC}/{du}) C^{-1} \in \operatorname {Lie} \operatorname {LG}'(A)$ correspond to the endomorphism given by ![]() $ ({ d C_V}/{du}) C_V^{-1}$ for
$ ({ d C_V}/{du}) C_V^{-1}$ for ![]() $V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G')$ under the equivalence of Example 2.2.1(c).
$V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G')$ under the equivalence of Example 2.2.1(c).
It is straightforward to verify that the ![]() $ ({ d C_V}/{du}) C_V^{-1}$ for
$ ({ d C_V}/{du}) C_V^{-1}$ for ![]() $V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G')$ are compatible with exact sequences and tensor products, so the definition is valid. By Remark 4.1.12, for
$V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G')$ are compatible with exact sequences and tensor products, so the definition is valid. By Remark 4.1.12, for ![]() $C = [\phi _\mathfrak {P}]_\beta$ we have
$C = [\phi _\mathfrak {P}]_\beta$ we have
Remark 4.1.14 The individual terms of ![]() $ ({d C}/{du }) C^{-1}$ have no intrinsic meaning, but overall expression behaves as the Leibniz rule would formally predict:
$ ({d C}/{du }) C^{-1}$ have no intrinsic meaning, but overall expression behaves as the Leibniz rule would formally predict:
This can be checked on ![]() $V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$.
$V \in {^f} \hspace {-2pt} \operatorname {Rep}_\Lambda (G)$.
4.2 Approximating the monodromy condition
We now want to study the monodromy condition in families and ![]() $p$-adically approximate it. We apply this to families of deformations such as that over
$p$-adically approximate it. We apply this to families of deformations such as that over ![]() $R^{\leqslant \mu, \beta, \square }_{\overline {\mathfrak {P}}}$. We follow the setup in [Reference Le, Le Hung, Levin and MorraLLHLM23, § 7.1].
$R^{\leqslant \mu, \beta, \square }_{\overline {\mathfrak {P}}}$. We follow the setup in [Reference Le, Le Hung, Levin and MorraLLHLM23, § 7.1].
Let ![]() $R$ be a flat local Noetherian
$R$ be a flat local Noetherian ![]() $\Lambda$-algebra with finite residue field that is
$\Lambda$-algebra with finite residue field that is ![]() $p$-adically complete. Define
$p$-adically complete. Define
which is naturally a subring of ![]() $(K \otimes _{\mathbf {Z}_p} R)[\![u]\!]$. Clearly, we have an inclusion
$(K \otimes _{\mathbf {Z}_p} R)[\![u]\!]$. Clearly, we have an inclusion ![]() $\mathcal {O}^{{\operatorname {rig}}} \subset \mathcal {O}^{{\operatorname {rig}}}_R$ and
$\mathcal {O}^{{\operatorname {rig}}} \subset \mathcal {O}^{{\operatorname {rig}}}_R$ and ![]() $\mathfrak {S}_R \rightarrow \mathcal {O}^{{\operatorname {rig}}}_R$. The operators
$\mathfrak {S}_R \rightarrow \mathcal {O}^{{\operatorname {rig}}}_R$. The operators ![]() $\varphi$ and
$\varphi$ and ![]() $N_{\nabla }$ extend to
$N_{\nabla }$ extend to ![]() $\mathcal {O}^{{\operatorname {rig}}}_R$ with trivial action on the coefficients. Note that for any
$\mathcal {O}^{{\operatorname {rig}}}_R$ with trivial action on the coefficients. Note that for any ![]() $f \in \mathcal {O}^{{\operatorname {rig}}}_R$, we can evaluate
$f \in \mathcal {O}^{{\operatorname {rig}}}_R$, we can evaluate ![]() $f$ at
$f$ at ![]() $u = p$ to get an element of
$u = p$ to get an element of ![]() $K \otimes _{\mathbf {Z}_p} R$ which we denote by
$K \otimes _{\mathbf {Z}_p} R$ which we denote by ![]() $f|_{u = p}$.
$f|_{u = p}$.
Fix a ![]() $G$-Kisin module
$G$-Kisin module ![]() $\mathfrak {P}$ with coefficients in
$\mathfrak {P}$ with coefficients in ![]() $R$, a trivialization of
$R$, a trivialization of ![]() $\mathfrak {P}$, and a type
$\mathfrak {P}$, and a type ![]() $\mu$ for
$\mu$ for ![]() $G$. Assume that
$G$. Assume that ![]() $\mathfrak {P}$ has type
$\mathfrak {P}$ has type ![]() $\leqslant \mu$, and as usual set
$\leqslant \mu$, and as usual set ![]() $h_{\mu } = \max _{\alpha \in \Phi _{ G'}} \langle \mu, \alpha \rangle$. We frequently use Lemma 3.1.8, that since
$h_{\mu } = \max _{\alpha \in \Phi _{ G'}} \langle \mu, \alpha \rangle$. We frequently use Lemma 3.1.8, that since ![]() $\mathfrak {P}$ has type
$\mathfrak {P}$ has type ![]() $\leqslant \mu$, then
$\leqslant \mu$, then ![]() $\mathfrak {P}(\operatorname {Lie} G)$ has height in
$\mathfrak {P}(\operatorname {Lie} G)$ has height in ![]() $[-h_{\mu }, h_{\mu }]$.
$[-h_{\mu }, h_{\mu }]$.
The same argument as in Proposition 4.1.7 using [Reference Le, Le Hung, Levin and MorraLLHLM23, Proposition 7.1.3(1)] shows that ![]() $\mathfrak {P}^{{\operatorname {rig}}}[1/\lambda ]$ (defined at the beginning of § 4.1) admits a unique derivation
$\mathfrak {P}^{{\operatorname {rig}}}[1/\lambda ]$ (defined at the beginning of § 4.1) admits a unique derivation ![]() $N_{\mathfrak {P}}$ such that
$N_{\mathfrak {P}}$ such that ![]() $N_{\mathfrak {P}} \equiv 0 \mod u$. Note that
$N_{\mathfrak {P}} \equiv 0 \mod u$. Note that ![]() $N_{\mathfrak {P}}$ interpolates the connections at all the finite flat
$N_{\mathfrak {P}}$ interpolates the connections at all the finite flat ![]() $\Lambda$-algebra points of
$\Lambda$-algebra points of ![]() $R$.
$R$.
Let ![]() $C \in G(\mathfrak {S}_R[1/E(u)])$ correspond to
$C \in G(\mathfrak {S}_R[1/E(u)])$ correspond to ![]() $\phi _\mathfrak {P}$. Trivialize the torsor of derivations by
$\phi _\mathfrak {P}$. Trivialize the torsor of derivations by ![]() $N_\mathfrak {P}^{\operatorname {triv}}$, and let
$N_\mathfrak {P}^{\operatorname {triv}}$, and let ![]() $N_\infty$ and
$N_\infty$ and ![]() $N_1$ be as in Corollary 4.1.8; in
$N_1$ be as in Corollary 4.1.8; in ![]() $\mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_R[1/\lambda ]}$, we have
$\mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_R[1/\lambda ]}$, we have
Definition 4.2.1 Let ![]() $N_0 := 0$ and for
$N_0 := 0$ and for ![]() $i > 0$, inductively define
$i > 0$, inductively define
Furthermore, set ![]() $L_1(C) := ({E(u)^{h_{\mu }}}/{u \lambda }) N_1 = - E(u)^{h_\mu } ({dC}/{du}) C^{-1}$.
$L_1(C) := ({E(u)^{h_{\mu }}}/{u \lambda }) N_1 = - E(u)^{h_\mu } ({dC}/{du}) C^{-1}$.
Lemma 4.2.2 The sequence ![]() $\{N_i\}$ converges to
$\{N_i\}$ converges to ![]() $N_\infty$ in
$N_\infty$ in ![]() $\mathfrak {g}_{(K \otimes _{\mathbf {Z}_p} R)[\![u ] \!]}$ in the
$\mathfrak {g}_{(K \otimes _{\mathbf {Z}_p} R)[\![u ] \!]}$ in the ![]() $u$-adic topology.
$u$-adic topology.
Proof. When ![]() $G = \operatorname {GL}_n$, this follows from [Reference Le, Le Hung, Levin and MorraLLHLM23, Proposition 7.1.3(2)]. In general, one may check the result on each
$G = \operatorname {GL}_n$, this follows from [Reference Le, Le Hung, Levin and MorraLLHLM23, Proposition 7.1.3(2)]. In general, one may check the result on each ![]() $V \in {^f} \hspace {-2pt} \operatorname {Rep}(G)$.
$V \in {^f} \hspace {-2pt} \operatorname {Rep}(G)$.
Proposition 4.2.3 The ![]() $G$-Kisin module
$G$-Kisin module ![]() $\mathfrak {P}$ satisfies the monodromy condition if and only if
$\mathfrak {P}$ satisfies the monodromy condition if and only if ![]() $N_\infty$ has no poles at
$N_\infty$ has no poles at ![]() $u=p$.
$u=p$.
Proof. When ![]() $G = \operatorname {GL}_n$, this is [Reference Bergdall and LevinBL22, Proposition 2.2.4]. The general case follows as both conditions may be checked on each
$G = \operatorname {GL}_n$, this is [Reference Bergdall and LevinBL22, Proposition 2.2.4]. The general case follows as both conditions may be checked on each ![]() $V \in {^f} \hspace {-2pt} \operatorname {Rep}(G)$.
$V \in {^f} \hspace {-2pt} \operatorname {Rep}(G)$.
Thus, we are reduced to studying the condition that ![]() $N_{\infty }$ has no poles at
$N_{\infty }$ has no poles at ![]() $u = p$. We aim to show that the condition that
$u = p$. We aim to show that the condition that ![]() $N_1$ has no poles at
$N_1$ has no poles at ![]() $u = p$ is a good approximation to this condition when
$u = p$ is a good approximation to this condition when ![]() $h_{\mu } < p-1$. To make this precise, we have to look more carefully at the sequence
$h_{\mu } < p-1$. To make this precise, we have to look more carefully at the sequence ![]() $N_i$.
$N_i$.
Lemma 4.2.4 Assume ![]() $\mathfrak {P}$ has type
$\mathfrak {P}$ has type ![]() $\leqslant \mu$ and that
$\leqslant \mu$ and that ![]() $R[1/p]$ is reduced. Then:
$R[1/p]$ is reduced. Then:
(i)
 $L_1(C) \in \mathfrak {g}_{\mathfrak {S}_R}$;
$L_1(C) \in \mathfrak {g}_{\mathfrak {S}_R}$;(ii)
 $E(u)^{h_\mu } Ad_G(C) (\mathfrak {g}_{\mathfrak {S}_R} )\subset \mathfrak {g}_{\mathfrak {S}_R}$ and
$E(u)^{h_\mu } Ad_G(C) (\mathfrak {g}_{\mathfrak {S}_R} )\subset \mathfrak {g}_{\mathfrak {S}_R}$ and  $E(u)^{h_\mu } Ad_G(C) (\mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_R} )\subset \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_R}$;
$E(u)^{h_\mu } Ad_G(C) (\mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_R} )\subset \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_R}$;(iii)
 $\lambda ^{h_{\mu }-1} N_{\infty } \in \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_R}$.
$\lambda ^{h_{\mu }-1} N_{\infty } \in \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_R}$.
Proof. As can be checked on any faithful representation, ![]() $L_1(C) \in \mathfrak {g}_{\mathfrak {S}_{R}}[1/E(u)]$. The condition that
$L_1(C) \in \mathfrak {g}_{\mathfrak {S}_{R}}[1/E(u)]$. The condition that ![]() $L_1(C) \in \mathfrak {g}_{\mathfrak {S}_R}$ is then a Zariski closed condition on
$L_1(C) \in \mathfrak {g}_{\mathfrak {S}_R}$ is then a Zariski closed condition on ![]() $R$. Since
$R$. Since ![]() $R$ is
$R$ is ![]() $\Lambda$-flat and reduced, it suffices to check that condition on the
$\Lambda$-flat and reduced, it suffices to check that condition on the ![]() $\overline {L}$-points of
$\overline {L}$-points of ![]() $R$. If
$R$. If ![]() $x$ is any such point, let
$x$ is any such point, let ![]() $C_x$ denote the base change of
$C_x$ denote the base change of ![]() $x$ to
$x$ to ![]() $\overline {L}$.
$\overline {L}$.
Since ![]() $\mathfrak {P}$ has type
$\mathfrak {P}$ has type ![]() $\leqslant \mu$, there exists
$\leqslant \mu$, there exists ![]() $\mu ' \leqslant \mu$ such that
$\mu ' \leqslant \mu$ such that ![]() $C_x = K_1 E(u)^{\mu '} K_2$ where
$C_x = K_1 E(u)^{\mu '} K_2$ where ![]() $K_1, K_2 \in \textrm {L}^+G'(\overline {L})$. Applying Remark 4.1.14, we have
$K_1, K_2 \in \textrm {L}^+G'(\overline {L})$. Applying Remark 4.1.14, we have
We directly see that ![]() $L_1(K_1)$ and
$L_1(K_1)$ and ![]() $E(u) ({ d E(u)^{\mu '}}/{du}) E(u)^{-\mu '}$ are in
$E(u) ({ d E(u)^{\mu '}}/{du}) E(u)^{-\mu '}$ are in ![]() $\mathfrak {g}_{\mathfrak {S}_{\overline {L}}}$. For the third term, note that
$\mathfrak {g}_{\mathfrak {S}_{\overline {L}}}$. For the third term, note that ![]() $ ({dK_2}/{du}) K_2^{-1} \in \mathfrak {g}_{\mathfrak {S}_{\overline {L}}}$ and since
$ ({dK_2}/{du}) K_2^{-1} \in \mathfrak {g}_{\mathfrak {S}_{\overline {L}}}$ and since ![]() $\mu ' \leqslant \mu$, we know
$\mu ' \leqslant \mu$, we know ![]() $E(u)^{h_{\mu }} \operatorname {Ad}_G(K_1 E(u)^{\mu '})$ preserves
$E(u)^{h_{\mu }} \operatorname {Ad}_G(K_1 E(u)^{\mu '})$ preserves ![]() $\mathfrak {g}_{\mathfrak {S}_{\overline {L}}}$. Thus, we conclude
$\mathfrak {g}_{\mathfrak {S}_{\overline {L}}}$. Thus, we conclude ![]() $L_1(C_x) \in \mathfrak {g}_{\mathfrak {S}_{\overline {L}}}$.
$L_1(C_x) \in \mathfrak {g}_{\mathfrak {S}_{\overline {L}}}$.
Since ![]() $\mathfrak {P}$ has type
$\mathfrak {P}$ has type ![]() $\leqslant \mu$, we see that
$\leqslant \mu$, we see that ![]() $\mathfrak {P}(\operatorname {Lie} G)$ has height in
$\mathfrak {P}(\operatorname {Lie} G)$ has height in ![]() $[-h_\mu,h_\mu ]$ which gives part (ii).
$[-h_\mu,h_\mu ]$ which gives part (ii).
For the last part, it suffices to show ![]() $\lambda ^{h_{\mu }-1} N_{i} \in \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_R}$ which we prove by induction on
$\lambda ^{h_{\mu }-1} N_{i} \in \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_R}$ which we prove by induction on ![]() $i$. The base case follows from part (i). Since
$i$. The base case follows from part (i). Since ![]() $N_{i+1} = N_i + E(u) \operatorname {Ad}_G(C) \big ( \varphi (N_{i} - N_{i-1}) \big ),$ it suffices to show that if
$N_{i+1} = N_i + E(u) \operatorname {Ad}_G(C) \big ( \varphi (N_{i} - N_{i-1}) \big ),$ it suffices to show that if ![]() $\lambda ^{h_{\mu }-1} N_{i} \in \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_R}$ then
$\lambda ^{h_{\mu }-1} N_{i} \in \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_R}$ then ![]() $E(u) \lambda ^{h_{\mu }-1} \operatorname {Ad}_G(C) \big ( \varphi (N_{i}) \big ) \in \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_R}$. This follows from part (ii) using that
$E(u) \lambda ^{h_{\mu }-1} \operatorname {Ad}_G(C) \big ( \varphi (N_{i}) \big ) \in \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_R}$. This follows from part (ii) using that
Since ![]() $\lambda$ has simple pole at
$\lambda$ has simple pole at ![]() $u = p$, the condition that
$u = p$, the condition that ![]() $N_1$ has no poles at
$N_1$ has no poles at ![]() $u = p$ is equivalent to
$u = p$ is equivalent to ![]() $L_1(C)$ having a zero of order at least
$L_1(C)$ having a zero of order at least ![]() $h_{\mu }-1$. Similarly, by Lemma 4.2.4(iii), the monodromy condition is equivalent to
$h_{\mu }-1$. Similarly, by Lemma 4.2.4(iii), the monodromy condition is equivalent to ![]() $E(u)^{h_\mu -1}N_{\infty }$ having a zero of order at least
$E(u)^{h_\mu -1}N_{\infty }$ having a zero of order at least ![]() $h_\mu -1$ at
$h_\mu -1$ at ![]() $u = p$.
$u = p$.
Given an element of element ![]() $X = (X_\sigma )_{\sigma \in \mathcal {J}} \in \mathfrak {g}_{K \otimes _{\Lambda } R} = \prod _{\sigma \in \mathcal {J}} \mathfrak {g}_R$, we say the entries of
$X = (X_\sigma )_{\sigma \in \mathcal {J}} \in \mathfrak {g}_{K \otimes _{\Lambda } R} = \prod _{\sigma \in \mathcal {J}} \mathfrak {g}_R$, we say the entries of ![]() $X$ are the coefficients of each
$X$ are the coefficients of each ![]() $X_\sigma$ with respect to a fixed basis for
$X_\sigma$ with respect to a fixed basis for ![]() $\mathfrak {g}$ over
$\mathfrak {g}$ over ![]() $\Lambda$.
$\Lambda$.
Definition 4.2.5 Let ![]() $\widetilde {I}_{N_{\infty }}$ denote the ideal in
$\widetilde {I}_{N_{\infty }}$ denote the ideal in ![]() $R[1/p]$ generated by the entries of
$R[1/p]$ generated by the entries of ![]() $ { d^i \big ( E(u)^{h_\mu -1} N_{\infty } \big )}/{du^i} |_{u=p}$ for
$ { d^i \big ( E(u)^{h_\mu -1} N_{\infty } \big )}/{du^i} |_{u=p}$ for ![]() $0 \leqslant i \leqslant h_\mu -2$. Furthermore, define
$0 \leqslant i \leqslant h_\mu -2$. Furthermore, define
so ![]() $\operatorname {Spec} R/I_{N_{\infty }}$ is closure of the locus on the generic fiber satisfying the monodromy condition.
$\operatorname {Spec} R/I_{N_{\infty }}$ is closure of the locus on the generic fiber satisfying the monodromy condition.
Define ![]() $I_{N_1} \subset R$ to be the ideal generated by the entries of
$I_{N_1} \subset R$ to be the ideal generated by the entries of ![]() $ ({ d^i L_1(C)}/{du^i}) |_{u=p}$ for
$ ({ d^i L_1(C)}/{du^i}) |_{u=p}$ for ![]() $0 \leqslant i \leqslant h_\mu -2$.
$0 \leqslant i \leqslant h_\mu -2$.
Our goal is to ![]() $p$-adically approximate
$p$-adically approximate ![]() $I_{N_{\infty }}$ and relate it to
$I_{N_{\infty }}$ and relate it to ![]() $I_{N_1}$ by studying the condition on the pole of
$I_{N_1}$ by studying the condition on the pole of ![]() $N_1$. This will yield our main theorem.
$N_1$. This will yield our main theorem.
Theorem 4.2.6 Let ![]() $\mathfrak {P}$ be a
$\mathfrak {P}$ be a ![]() $G$-Kisin module with coefficients in a complete flat local Noetherian
$G$-Kisin module with coefficients in a complete flat local Noetherian ![]() $\Lambda$-algebra
$\Lambda$-algebra ![]() $R$ with finite residue field. Assume
$R$ with finite residue field. Assume ![]() $\mathfrak {P}$ has type
$\mathfrak {P}$ has type ![]() $\leqslant \mu$, that
$\leqslant \mu$, that ![]() $h_{\mu } < p-1$, and that
$h_{\mu } < p-1$, and that ![]() $R[1/p]$ is reduced. Then
$R[1/p]$ is reduced. Then
We prove this in § 4.3. The key idea is to control the ![]() $p$-divisibility of terms in a series relating
$p$-divisibility of terms in a series relating ![]() $N_\infty$ to
$N_\infty$ to ![]() $N_1$.
$N_1$.
Definition 4.2.7 Let ![]() $\mathfrak {P}$ be a
$\mathfrak {P}$ be a ![]() $G$-Kisin module with coefficients in a
$G$-Kisin module with coefficients in a ![]() $\Lambda$-algebra
$\Lambda$-algebra ![]() $A$ of characteristic
$A$ of characteristic ![]() $p$. Let
$p$. Let ![]() $C$ correspond to
$C$ correspond to ![]() $\varphi _\mathfrak {P}$ upon choice of trivialization. We say that
$\varphi _\mathfrak {P}$ upon choice of trivialization. We say that ![]() $\mathfrak {P}$ satisfies the mod-
$\mathfrak {P}$ satisfies the mod-![]() $p$ monodromy condition provided that
$p$ monodromy condition provided that ![]() $L_1(C)$ has a zero of order at least
$L_1(C)$ has a zero of order at least ![]() $h_\mu -1$ at
$h_\mu -1$ at ![]() $u=p$.
$u=p$.
It is straightforward to verify that this notion is independent of the choice of trivialization, and equivalent to the condition that ![]() $ ({dC}/{du}) C^{-1} \in ({1}/{u}) \mathfrak {g}_{\mathfrak {S}_A}$.
$ ({dC}/{du}) C^{-1} \in ({1}/{u}) \mathfrak {g}_{\mathfrak {S}_A}$.
Corollary 4.2.8 Assume ![]() $h_\mu < p-1$ and that
$h_\mu < p-1$ and that ![]() $R[1/p]$ is reduced. The base change
$R[1/p]$ is reduced. The base change ![]() $\mathfrak {P} \otimes _{\mathfrak {S}_R} \mathfrak {S}_{R/ (p,I_{N_\infty })}$ satisfies the mod-
$\mathfrak {P} \otimes _{\mathfrak {S}_R} \mathfrak {S}_{R/ (p,I_{N_\infty })}$ satisfies the mod-![]() $p$ monodromy condition.
$p$ monodromy condition.
Proof. Theorem 4.2.6 shows ![]() $\operatorname {Spf} R/(I_{N_\infty },p) \hookrightarrow \operatorname {Spf} R/(I_{N_1},p)$.
$\operatorname {Spf} R/(I_{N_\infty },p) \hookrightarrow \operatorname {Spf} R/(I_{N_1},p)$.
4.3 Proof of Theorem 4.2.6
We continue the notation of the previous subsection and set ![]() $h := h_\mu$. Throughout we assume that
$h := h_\mu$. Throughout we assume that ![]() $R[1/p]$ is reduced. We begin with some preliminaries.
$R[1/p]$ is reduced. We begin with some preliminaries.
Lemma 4.3.1 Assume that ![]() $\mathfrak {P}(\operatorname {Lie} G)$ has height in
$\mathfrak {P}(\operatorname {Lie} G)$ has height in ![]() $[-h, h]$. Then:
$[-h, h]$. Then:
(i)
 $E(u)^h N_1 \in u \lambda \mathfrak {g}_{\mathcal {O}_R^{\operatorname {rig}}}$;
$E(u)^h N_1 \in u \lambda \mathfrak {g}_{\mathcal {O}_R^{\operatorname {rig}}}$;(ii) fix
 $j< p$ and
$j< p$ and  $X \in \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_R}$; if
$X \in \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_R}$; if  $ ({d^i X}/{du^i}) |_{u=p} \in p^r \mathfrak {g}_{W(k) \otimes _{\mathbf {Z}_p} R}$ for all
$ ({d^i X}/{du^i}) |_{u=p} \in p^r \mathfrak {g}_{W(k) \otimes _{\mathbf {Z}_p} R}$ for all  $0 \leqslant i \leqslant j$, then for any
$0 \leqslant i \leqslant j$, then for any  $i \leqslant j$
$i \leqslant j$
 \[ \frac{ d^i \big( E(u)^h Ad_G(C) (X) \big)}{du^i} \bigg|_{u=p} \in p^r \mathfrak{g}_{W(k) \otimes_{\mathbf{Z}_p} R}. \]
\[ \frac{ d^i \big( E(u)^h Ad_G(C) (X) \big)}{du^i} \bigg|_{u=p} \in p^r \mathfrak{g}_{W(k) \otimes_{\mathbf{Z}_p} R}. \]
Proof. The first statement follows from Lemma 4.2.4(i).
For the second statement, we can expand ![]() $X = \sum _{i \geqslant 0} X_i ({E(u)^i} /{i!})$ with
$X = \sum _{i \geqslant 0} X_i ({E(u)^i} /{i!})$ with ![]() $X_i \in p^r \mathfrak {g}_{W(k) \otimes _{\mathbf {Z}_p} R}$ for
$X_i \in p^r \mathfrak {g}_{W(k) \otimes _{\mathbf {Z}_p} R}$ for ![]() $i \leqslant j$ and otherwise
$i \leqslant j$ and otherwise ![]() $X_i \in \mathfrak {g}_{K \otimes _{\mathbf {Z}_p} R}$. By Lemma 4.2.4(ii), we see that
$X_i \in \mathfrak {g}_{K \otimes _{\mathbf {Z}_p} R}$. By Lemma 4.2.4(ii), we see that ![]() $E(u)^h Ad_G(C)(X_i) \in p^r \mathfrak {g}_{\mathfrak {S}_R}$ for
$E(u)^h Ad_G(C)(X_i) \in p^r \mathfrak {g}_{\mathfrak {S}_R}$ for ![]() $i \leqslant j$. For any
$i \leqslant j$. For any ![]() $i \leqslant j$ we conclude that
$i \leqslant j$ we conclude that
 \[ \frac{ d^i \big( E(u)^h Ad_G(C) (X) \big)}{du^i} \bigg|_{u=p} \in p^r \mathfrak{g}_{W(k) \otimes_{\mathbf{Z}_p} R}. \]
\[ \frac{ d^i \big( E(u)^h Ad_G(C) (X) \big)}{du^i} \bigg|_{u=p} \in p^r \mathfrak{g}_{W(k) \otimes_{\mathbf{Z}_p} R}. \]
Definition 4.3.2 We define ![]() $\mathcal {A}_C : \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_R} \to \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_R}$ by
$\mathcal {A}_C : \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_R} \to \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_R}$ by ![]() $\mathcal {A}_C(X) = E(u)^h \operatorname {Ad}_G(C) (\varphi (X))$. Furthermore, define
$\mathcal {A}_C(X) = E(u)^h \operatorname {Ad}_G(C) (\varphi (X))$. Furthermore, define ![]() $L_2(C) := \mathcal {A}_C(L_1(C)) = E(u)^h \operatorname {Ad}_G(C) ( \varphi (L_1(C)))$.
$L_2(C) := \mathcal {A}_C(L_1(C)) = E(u)^h \operatorname {Ad}_G(C) ( \varphi (L_1(C)))$.
Note that ![]() $\mathcal {A}_C$ is well defined and that
$\mathcal {A}_C$ is well defined and that ![]() $L_2(C)$ lies in
$L_2(C)$ lies in ![]() $\mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_R}$ by Lemma 4.2.4(ii).
$\mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_R}$ by Lemma 4.2.4(ii).
Remark 4.3.3 When ![]() $G=\operatorname {GL}_n$, using Remark 4.1.12 we see
$G=\operatorname {GL}_n$, using Remark 4.1.12 we see ![]() $L_1(C) = -E(u)^h ({dC}/{du}) C^{-1}$ and
$L_1(C) = -E(u)^h ({dC}/{du}) C^{-1}$ and ![]() $L_2(C) = E(u)^h C \varphi ( L_1(C)) C^{-1}$.
$L_2(C) = E(u)^h C \varphi ( L_1(C)) C^{-1}$.
Now we let
 \begin{equation} z_0 := -\frac{ u \varphi(\lambda)}{p} \quad \text{and} \quad z_i := -\frac{u^{p^i} \varphi^{i+1}(\lambda)}{p \prod_{j=1}^i \varphi^j(E(u))^{h-1} }. \end{equation}
\begin{equation} z_0 := -\frac{ u \varphi(\lambda)}{p} \quad \text{and} \quad z_i := -\frac{u^{p^i} \varphi^{i+1}(\lambda)}{p \prod_{j=1}^i \varphi^j(E(u))^{h-1} }. \end{equation}Lemma 4.3.4 Letting ![]() $\mathcal {A}_C^i$ denote the
$\mathcal {A}_C^i$ denote the ![]() $i$-fold composition of
$i$-fold composition of ![]() $\mathcal {A}_C$, we have that
$\mathcal {A}_C$, we have that
and that
 \begin{equation} E(u)^{h-1} N_\infty = E(u)^{h-1} N_1 + \sum_{i=1}^\infty E(u)^{h-1}(N_{i+1} - N_i) = z_0 L_1(C) + \sum_{i=1}^\infty z_i \mathcal{A}_C^i(L_1(C)). \end{equation}
\begin{equation} E(u)^{h-1} N_\infty = E(u)^{h-1} N_1 + \sum_{i=1}^\infty E(u)^{h-1}(N_{i+1} - N_i) = z_0 L_1(C) + \sum_{i=1}^\infty z_i \mathcal{A}_C^i(L_1(C)). \end{equation}
Furthermore, we have that ![]() $\mathcal {A}_C^i(L_1(C)) \in \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_R}$.
$\mathcal {A}_C^i(L_1(C)) \in \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_R}$.
Proof. We directly see that ![]() $E(u)^{h-1} N_1 = z_0 L_1(C)$, and then the first equation follows from induction using (4.2.1). The second equation telescopes. The last claim follows from Lemma 4.2.4(i).
$E(u)^{h-1} N_1 = z_0 L_1(C)$, and then the first equation follows from induction using (4.2.1). The second equation telescopes. The last claim follows from Lemma 4.2.4(i).
We now collect together information about ![]() $z_0$ and the
$z_0$ and the ![]() $z_i$. Let
$z_i$. Let ![]() $v_p$ denote the
$v_p$ denote the ![]() $p$-adic valuation on
$p$-adic valuation on ![]() $\mathbf {Z}_p$ normalized so
$\mathbf {Z}_p$ normalized so ![]() $v_p(p) = 1$.
$v_p(p) = 1$.
Lemma 4.3.5 Let ![]() $i \geqslant 1$.
$i \geqslant 1$.
(i) We have that
 $\varphi ^i(\lambda )|_{u=p}$ is a unit in
$\varphi ^i(\lambda )|_{u=p}$ is a unit in  $\mathbf {Z}_p$, and that for
$\mathbf {Z}_p$, and that for  $0 < n < p$
$0 < n < p$
 \[ \frac{d ^n \varphi^i(\lambda)}{du^n} \bigg|_{u=p} = -\frac{(p^i-1)!}{(p^i-n)!} p^{p^i+(i-1)-n} + O(p^{p^i+i-n}). \]
\[ \frac{d ^n \varphi^i(\lambda)}{du^n} \bigg|_{u=p} = -\frac{(p^i-1)!}{(p^i-n)!} p^{p^i+(i-1)-n} + O(p^{p^i+i-n}). \]
(ii) For
 $1 < n < p$, we have that
$1 < n < p$, we have that
 \[ v_p\big( z_0|_{u=p} \big) =0, \quad v_p \bigg( \frac{dz_0}{du}\bigg|_{u=p} \bigg) = -1 ,\quad \text{and} \quad v_p \bigg( \frac{d^{n}z_0}{du^n} \bigg|_{u=p} \bigg) = p-n. \]
\[ v_p\big( z_0|_{u=p} \big) =0, \quad v_p \bigg( \frac{dz_0}{du}\bigg|_{u=p} \bigg) = -1 ,\quad \text{and} \quad v_p \bigg( \frac{d^{n}z_0}{du^n} \bigg|_{u=p} \bigg) = p-n. \]
(iii) For
 $0 < n < p-1$, we have that
$0 < n < p-1$, we have that
 \[ v_p \big( z_i \big) \geqslant p^i - i(h-1)-1 \quad \text{and} \quad v_p \bigg( \frac{d^n z_i}{du^n} \bigg) \geqslant p^i + \min(i,p) - n - i (h-1) -1 . \]
\[ v_p \big( z_i \big) \geqslant p^i - i(h-1)-1 \quad \text{and} \quad v_p \bigg( \frac{d^n z_i}{du^n} \bigg) \geqslant p^i + \min(i,p) - n - i (h-1) -1 . \]
Proof. (i) This an elementary calculation using the product rule on
 \[ \varphi^i(\lambda) = \prod_{j=i}^\infty \frac{u^{p^j}-p}{-p}. \]
\[ \varphi^i(\lambda) = \prod_{j=i}^\infty \frac{u^{p^j}-p}{-p}. \]
(ii) This will follow using part (i). The first claim is immediate. The second follows from
For the third, note that
and that ![]() $1 + (n-1)^{-1} \not \equiv 0 \mod {p}$ when
$1 + (n-1)^{-1} \not \equiv 0 \mod {p}$ when ![]() $1< n < p$.
$1< n < p$.
(iii) An elementary analysis using the product rule shows that for ![]() $0 < n < p$, we have
$0 < n < p$, we have
 \[ v_p \bigg( \frac{d^n}{du^n} \bigg( \prod_{j=1}^i \varphi^j(E(u)/(-p))^{1-h} \bigg)\bigg|_{u=p} \bigg) \geqslant p-n . \]
\[ v_p \bigg( \frac{d^n}{du^n} \bigg( \prod_{j=1}^i \varphi^j(E(u)/(-p))^{1-h} \bigg)\bigg|_{u=p} \bigg) \geqslant p-n . \]
Furthermore, ![]() $\prod _{j=1}^i \varphi ^j(E(u)/(-p))^{1-h}$ evaluated at
$\prod _{j=1}^i \varphi ^j(E(u)/(-p))^{1-h}$ evaluated at ![]() $u=p$ is a
$u=p$ is a ![]() $p$-adic unit. Combining this with part (i), we see using the product rule that for
$p$-adic unit. Combining this with part (i), we see using the product rule that for ![]() $0< n < p$ the
$0< n < p$ the ![]() $n$th derivative of
$n$th derivative of
 \[ z_i = (-p)^{-i (h-1)-1} u^{p^i} \cdot \varphi^{i+1}(\lambda) \cdot \prod_{j=1}^i \varphi^j(E(u)/(-p))^{1-h} \]
\[ z_i = (-p)^{-i (h-1)-1} u^{p^i} \cdot \varphi^{i+1}(\lambda) \cdot \prod_{j=1}^i \varphi^j(E(u)/(-p))^{1-h} \]
when evaluated at ![]() $u=p$ will have valuation at least
$u=p$ will have valuation at least ![]() $p^i + \min (i,p) - n - i (h-1) -1$. The statement about
$p^i + \min (i,p) - n - i (h-1) -1$. The statement about ![]() $z_i$ itself is elementary given the previous calculations.
$z_i$ itself is elementary given the previous calculations.
We now begin to analyze the monodromy condition to obtain information about its reduction modulo ![]() $p$. At first glance, it is not clear that the evaluation of derivatives of terms in (4.3.3) at
$p$. At first glance, it is not clear that the evaluation of derivatives of terms in (4.3.3) at ![]() $u=p$ even lie in
$u=p$ even lie in ![]() $\mathfrak {g}_{W(k) \otimes _{\Lambda } R}$, let alone are multiples of
$\mathfrak {g}_{W(k) \otimes _{\Lambda } R}$, let alone are multiples of ![]() $p$. For conciseness, we write
$p$. For conciseness, we write ![]() $\mathfrak {g}_R'$ instead of
$\mathfrak {g}_R'$ instead of ![]() $\mathfrak {g}_{W(k) \otimes _{\Lambda } R}$ in the following arguments.
$\mathfrak {g}_{W(k) \otimes _{\Lambda } R}$ in the following arguments.
Lemma 4.3.6 Suppose that ![]() $h < p-1$. Then there exists
$h < p-1$. Then there exists ![]() $\alpha _0 \in \mathbf {Z}_p^\times$ such that
$\alpha _0 \in \mathbf {Z}_p^\times$ such that
and for ![]() $0 < m < h$ we have that
$0 < m < h$ we have that
 \begin{equation} \sum_{j=0}^m \binom{m}{j} \frac{ d^j z_0 }{du^j}\bigg|_{u=p} \frac{d^{m-j} L_1(C)}{du^{m-j}} \bigg|_{u=p} + \sum_{j=0}^m \binom{m}{j} \frac{d^j z_1}{du^j} \bigg|_{u=p} \frac{d^{m-j} L_2(C)}{du^{m-j}} \bigg|_{u=p} \in (p^p,I_{N_\infty}) \mathfrak{g}_R'. \end{equation}
\begin{equation} \sum_{j=0}^m \binom{m}{j} \frac{ d^j z_0 }{du^j}\bigg|_{u=p} \frac{d^{m-j} L_1(C)}{du^{m-j}} \bigg|_{u=p} + \sum_{j=0}^m \binom{m}{j} \frac{d^j z_1}{du^j} \bigg|_{u=p} \frac{d^{m-j} L_2(C)}{du^{m-j}} \bigg|_{u=p} \in (p^p,I_{N_\infty}) \mathfrak{g}_R'. \end{equation}Proof. We begin by evaluating (4.3.3) at ![]() $u=p$. We see that:
$u=p$. We see that:
– on the left-hand side, the entries of
 $E(u)^{h-1} N_\infty$ are in
$E(u)^{h-1} N_\infty$ are in  $I_{N_\infty }$ by definition;
$I_{N_\infty }$ by definition;–
 $v_p(z_i |_{u=p}) \geqslant p^2 - 2h +1 \geqslant p^2 - 2p +3 \geqslant p$ for
$v_p(z_i |_{u=p}) \geqslant p^2 - 2h +1 \geqslant p^2 - 2p +3 \geqslant p$ for  $i \geqslant 2$ using Lemma 4.3.5(iii);
$i \geqslant 2$ using Lemma 4.3.5(iii);–
 $\mathcal {A}_C^i(L_1(C)) \in \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_R}$.
$\mathcal {A}_C^i(L_1(C)) \in \mathfrak {g}_{\mathcal {O}^{\operatorname {rig}}_R}$.
Thus, all of the terms with ![]() $i\geqslant 2$ on the right-hand side are multiples of
$i\geqslant 2$ on the right-hand side are multiples of ![]() $p^p$. Since
$p^p$. Since ![]() $\alpha _0 := z_0 |_{u=p}$ is in
$\alpha _0 := z_0 |_{u=p}$ is in ![]() $\mathbf {Z}_p^\times$ by Lemma 4.3.5(ii), (4.3.4) follows.
$\mathbf {Z}_p^\times$ by Lemma 4.3.5(ii), (4.3.4) follows.
The second statement follows a similar argument, beginning by evaluating the ![]() $m$th derivative of by (4.3.3) at
$m$th derivative of by (4.3.3) at ![]() $u=p$. Again, the entries on the left-hand side are in
$u=p$. Again, the entries on the left-hand side are in ![]() $I_{N_\infty }$. We apply the product rule to the terms with
$I_{N_\infty }$. We apply the product rule to the terms with ![]() $i \geqslant 2$: the
$i \geqslant 2$: the ![]() $m$th derivative of the
$m$th derivative of the ![]() $i$th term is
$i$th term is
 \[ \sum_{j=0}^m \binom{m}{j} \frac{d^j z_i}{du^j} \bigg|_{u=p} \frac{d^{m-j} \mathcal{A}_C^i(L_1(C))}{du^{m-j}} \bigg|_{u=p}. \]
\[ \sum_{j=0}^m \binom{m}{j} \frac{d^j z_i}{du^j} \bigg|_{u=p} \frac{d^{m-j} \mathcal{A}_C^i(L_1(C))}{du^{m-j}} \bigg|_{u=p}. \]
By Lemma 4.3.4, ![]() $\mathcal {A}^i_C(L_1(C)) |_{u=p}$ and its derivatives lie in
$\mathcal {A}^i_C(L_1(C)) |_{u=p}$ and its derivatives lie in ![]() $\mathfrak {g}_R'$. Lemma 4.3.5(iii) gives that for
$\mathfrak {g}_R'$. Lemma 4.3.5(iii) gives that for ![]() $0 < j < p-1$
$0 < j < p-1$
 \[ v_p\bigg(\frac{d^j z_i}{du^j} \bigg|_{u=p} \bigg) \geqslant p^i + \min(i,p) - i (h-1) -j -1. \]
\[ v_p\bigg(\frac{d^j z_i}{du^j} \bigg|_{u=p} \bigg) \geqslant p^i + \min(i,p) - i (h-1) -j -1. \]
It is straightforward to see this is greater than or equal to ![]() $p$ when
$p$ when ![]() $i >2$ as the
$i >2$ as the ![]() $p^i$ term dominates. When
$p^i$ term dominates. When ![]() $i=2$, the valuation is at least
$i=2$, the valuation is at least
The right-hand side is always at least ![]() $p$. (For
$p$. (For ![]() $j=0$, we already say that
$j=0$, we already say that ![]() $v_p(z_i |_{u=p}) \geqslant p$.) Thus, all the terms on the right-hand side of the
$v_p(z_i |_{u=p}) \geqslant p$.) Thus, all the terms on the right-hand side of the ![]() $m$th derivative of (4.3.3) at
$m$th derivative of (4.3.3) at ![]() $u=p$ with
$u=p$ with ![]() $i\geqslant 2$ are multiples of
$i\geqslant 2$ are multiples of ![]() $p^p$.
$p^p$.
Now expand ![]() $L_1(C) = \sum _{i=0}^\infty A_i E(u)^i$ with
$L_1(C) = \sum _{i=0}^\infty A_i E(u)^i$ with ![]() $A_i \in \mathfrak {g}'_R$; there exists
$A_i \in \mathfrak {g}'_R$; there exists ![]() $Q \in \mathfrak {g}'_{R [\![u ] \!]}$ such that
$Q \in \mathfrak {g}'_{R [\![u ] \!]}$ such that
Lemma 4.3.7 For a fixed positive integer ![]() $n < p$, if for all
$n < p$, if for all ![]() $0 \leqslant i \leqslant n$ we have
$0 \leqslant i \leqslant n$ we have
 \[ \displaystyle \frac{ d^i L_1(C)}{du^i} \bigg|_{u=p} \in (p^{n-i},I_{N_\infty}) \mathfrak{g}_R', \]
\[ \displaystyle \frac{ d^i L_1(C)}{du^i} \bigg|_{u=p} \in (p^{n-i},I_{N_\infty}) \mathfrak{g}_R', \]
then it follows that ![]() $\varphi (L_1(C))|_{u=p} \in p^n \mathfrak {g}_R'$ and that for
$\varphi (L_1(C))|_{u=p} \in p^n \mathfrak {g}_R'$ and that for ![]() $0 < i \leqslant n$
$0 < i \leqslant n$
 \[ \frac{ d^i \varphi(L_1(C))}{du^i} \bigg|_{u=p} \in (p^{p+ n -i},I_{N_\infty}) \mathfrak{g}_R'. \]
\[ \frac{ d^i \varphi(L_1(C))}{du^i} \bigg|_{u=p} \in (p^{p+ n -i},I_{N_\infty}) \mathfrak{g}_R'. \]
Proof. The hypothesis implies that ![]() $A_i \in (p^{n-i} ,I_{N_\infty })\mathfrak {g}_R'$ for
$A_i \in (p^{n-i} ,I_{N_\infty })\mathfrak {g}_R'$ for ![]() $0\leqslant i \leqslant n$. The first claim about
$0\leqslant i \leqslant n$. The first claim about ![]() $\varphi (L_1(C))|_{u=p} = A_0$ is immediate from (4.3.6). For the second statement, we look closer at
$\varphi (L_1(C))|_{u=p} = A_0$ is immediate from (4.3.6). For the second statement, we look closer at ![]() $Q(u)$. In particular, there exists
$Q(u)$. In particular, there exists ![]() $Q_2(u) \in \mathfrak {g}'_{R[\![u ] \!]}$ such that
$Q_2(u) \in \mathfrak {g}'_{R[\![u ] \!]}$ such that
Since ![]() $A_i \in (p^{n-i},I_{N_\infty }) \mathfrak {g}_R'$ for
$A_i \in (p^{n-i},I_{N_\infty }) \mathfrak {g}_R'$ for ![]() $0\leqslant i \leqslant n$, it follows that
$0\leqslant i \leqslant n$, it follows that ![]() $Q(u)|_{u = p} \in (p^{n-1},I_{N_\infty }) \mathfrak {g}_R'$. By inspecting derivatives we see that
$Q(u)|_{u = p} \in (p^{n-1},I_{N_\infty }) \mathfrak {g}_R'$. By inspecting derivatives we see that ![]() $ {d^i Q(u)}/{du^i} |_{u=p} \in (p^{p+1-i},I_{N_\infty }) \mathfrak {g}_R'$ for
$ {d^i Q(u)}/{du^i} |_{u=p} \in (p^{p+1-i},I_{N_\infty }) \mathfrak {g}_R'$ for ![]() $i>0$. Using the product rule to compute derivatives of
$i>0$. Using the product rule to compute derivatives of ![]() $u^p Q(u)$ gives the desired result about derivatives of
$u^p Q(u)$ gives the desired result about derivatives of ![]() $\varphi (L_1(C))$.
$\varphi (L_1(C))$.
Corollary 4.3.8 For fixed ![]() $n < p$, suppose for all
$n < p$, suppose for all ![]() $0 \leqslant i < n$, we know that
$0 \leqslant i < n$, we know that
 \[ \frac{ d^i L_1(C)}{du^i} \bigg|_{u=p} \in (p^{n-i},I_{N_\infty}) \mathfrak{g}_R'. \]
\[ \frac{ d^i L_1(C)}{du^i} \bigg|_{u=p} \in (p^{n-i},I_{N_\infty}) \mathfrak{g}_R'. \]
Then it follows that for all ![]() $0\leqslant i \leqslant n$, we have
$0\leqslant i \leqslant n$, we have
 \[ \frac{d^i L_2(C)}{du^i}\bigg|_{u=p} \in (p^{n},I_{N_\infty}) \mathfrak{g}_R'. \]
\[ \frac{d^i L_2(C)}{du^i}\bigg|_{u=p} \in (p^{n},I_{N_\infty}) \mathfrak{g}_R'. \]
Lemma 4.3.9 Suppose that ![]() $h < p-1$ and fix
$h < p-1$ and fix ![]() $n < h$. If for
$n < h$. If for ![]() $0 \leqslant i < n$, we know that
$0 \leqslant i < n$, we know that
 \[ \frac{d^i L_1(C)}{du^i} \bigg|_{u=p} \in (p^{n-i}, I_{N_\infty} ) \mathfrak{g}_R', \]
\[ \frac{d^i L_1(C)}{du^i} \bigg|_{u=p} \in (p^{n-i}, I_{N_\infty} ) \mathfrak{g}_R', \]
then for ![]() $0 \leqslant j < n+1$ we have that
$0 \leqslant j < n+1$ we have that
 \[ \frac{d^j L_1(C)}{du^j}\bigg|_{u=p} \in (p^{n+1-j}, I_{N_\infty} ) \mathfrak{g}_R'. \]
\[ \frac{d^j L_1(C)}{du^j}\bigg|_{u=p} \in (p^{n+1-j}, I_{N_\infty} ) \mathfrak{g}_R'. \]
Proof. Using Corollary 4.3.8, the hypothesis implies that
 \begin{equation} \frac{d^i L_2(C)}{du^i}\bigg|_{u=p} \in (p^{n}, I_{N_\infty}) \mathfrak{g}_R' \quad \text{for}\ 0 \leqslant i \leqslant n. \end{equation}
\begin{equation} \frac{d^i L_2(C)}{du^i}\bigg|_{u=p} \in (p^{n}, I_{N_\infty}) \mathfrak{g}_R' \quad \text{for}\ 0 \leqslant i \leqslant n. \end{equation}
By Lemma 4.3.5(iii), since ![]() $h < p-1$ we know that for
$h < p-1$ we know that for ![]() $0 < i < p$
$0 < i < p$
We now show that ![]() $ {d^m L_1(C)}/{du^m}|_{u=p} \in (p^{n+1-m}, I_{N_\infty }) \mathfrak {g}_R'$ for
$ {d^m L_1(C)}/{du^m}|_{u=p} \in (p^{n+1-m}, I_{N_\infty }) \mathfrak {g}_R'$ for ![]() $0 \leqslant m < n+1$ by induction on
$0 \leqslant m < n+1$ by induction on ![]() $m$.
$m$.
For the base case ![]() $m=0$, we know that
$m=0$, we know that ![]() $L_2(C)|_{u=p} \in (p^n, I_{N_\infty }) \mathfrak {g}_R'$, and that
$L_2(C)|_{u=p} \in (p^n, I_{N_\infty }) \mathfrak {g}_R'$, and that ![]() $v_p(z_1) >0$. Therefore, using (4.3.4) we conclude that
$v_p(z_1) >0$. Therefore, using (4.3.4) we conclude that ![]() $L_1(C)|_{u=p} \in (p^{n+1}, I_{N_\infty }) \mathfrak {g}_R'$ as desired.
$L_1(C)|_{u=p} \in (p^{n+1}, I_{N_\infty }) \mathfrak {g}_R'$ as desired.
For the inductive step, fix ![]() $0< m < n+1$ and suppose that for all
$0< m < n+1$ and suppose that for all ![]() $0 \leqslant j < m$,
$0 \leqslant j < m$,
 \[ \frac{d^j L_1(C)}{du^j}\bigg|_{u=p} \in (p^{n+1-j}, I_{N_\infty}) \mathfrak{g}_R'. \]
\[ \frac{d^j L_1(C)}{du^j}\bigg|_{u=p} \in (p^{n+1-j}, I_{N_\infty}) \mathfrak{g}_R'. \]
We consider each of the terms in (4.3.5). First, using (4.3.7) and (4.3.8) we see that
Second, for ![]() $0< i \leqslant m$ we see that
$0< i \leqslant m$ we see that
 \[ \frac{d^i z_1}{du^i} \bigg|_{u=p} \cdot \frac{d^{m-i} L_2(C)}{du^{m-i}} \bigg|_{u=p} \in (p^{n+3-i}, I_{N_\infty}) \mathfrak{g}_R' \subset (p^{n+1-m}, I_{N_\infty}) \mathfrak{g}_R'. \]
\[ \frac{d^i z_1}{du^i} \bigg|_{u=p} \cdot \frac{d^{m-i} L_2(C)}{du^{m-i}} \bigg|_{u=p} \in (p^{n+3-i}, I_{N_\infty}) \mathfrak{g}_R' \subset (p^{n+1-m}, I_{N_\infty}) \mathfrak{g}_R'. \]
Furthermore, for ![]() $0 < i \leqslant m$ we see that
$0 < i \leqslant m$ we see that
 \[ \frac{ d^i z_0 }{du^i}\bigg|_{u=p} \cdot \frac{d^{m-i} L_1(C)}{du^{m-i}} \bigg|_{u=p} \in ( p^{n+1 -m}, I_{N_\infty}) \mathfrak{g}_R' \]
\[ \frac{ d^i z_0 }{du^i}\bigg|_{u=p} \cdot \frac{d^{m-i} L_1(C)}{du^{m-i}} \bigg|_{u=p} \in ( p^{n+1 -m}, I_{N_\infty}) \mathfrak{g}_R' \]
using the inductive hypothesis and Lemma 4.3.5(ii). Then (4.3.5) plus the fact that ![]() $z_0 |_{u=p}$ is a unit imply that
$z_0 |_{u=p}$ is a unit imply that
which completes the induction.
Corollary 4.3.10 Suppose that ![]() $h < p-1$. Then for any
$h < p-1$. Then for any ![]() $0\leqslant i \leqslant h-1$, we have that
$0\leqslant i \leqslant h-1$, we have that
 \[ \frac{d^i L_1(C)}{du^i} \bigg|_{u=p} \in (p^{h-i}, I_{N_\infty} )\mathfrak{g}_R' \quad \text{and} \quad \frac{d^i L_2(C)}{du^i} \in (p^h, I_{N_\infty} )\mathfrak{g}_R' . \]
\[ \frac{d^i L_1(C)}{du^i} \bigg|_{u=p} \in (p^{h-i}, I_{N_\infty} )\mathfrak{g}_R' \quad \text{and} \quad \frac{d^i L_2(C)}{du^i} \in (p^h, I_{N_\infty} )\mathfrak{g}_R' . \]
Proof. The first part follows from induction using Lemma 4.3.9. The base case is that ![]() $L_1(C) \in (p, I_{N_\infty }) \mathfrak {g}_R'$, which follows from (4.3.4) and the information about
$L_1(C) \in (p, I_{N_\infty }) \mathfrak {g}_R'$, which follows from (4.3.4) and the information about ![]() $v_p(z_1|_{u=p})$ in Lemma 4.3.5. The statement about
$v_p(z_1|_{u=p})$ in Lemma 4.3.5. The statement about ![]() $L_2(C)$ is then Corollary 4.3.8.
$L_2(C)$ is then Corollary 4.3.8.
Proof of Theorem 4.2.6 It suffices to show that the entries of ![]() $ ({d^i L_1(C)}/{du^i}) |_{u=p}$ lie in
$ ({d^i L_1(C)}/{du^i}) |_{u=p}$ lie in ![]() $(I_{N_\infty },p)$ for
$(I_{N_\infty },p)$ for ![]() $0 \leqslant i \leqslant h-2$, which follows from Corollary 4.3.10.
$0 \leqslant i \leqslant h-2$, which follows from Corollary 4.3.10.
5. Affine Schubert varieties and monodromy
For this section, we allow ![]() $k$ to be any field and
$k$ to be any field and ![]() $G$ to be any split connected reductive group over
$G$ to be any split connected reductive group over ![]() $k$. Let
$k$. Let ![]() $G^{\mathrm {der}}$ denote its derived group with center
$G^{\mathrm {der}}$ denote its derived group with center ![]() $Z^{\mathrm {der}}$. Let
$Z^{\mathrm {der}}$. Let ![]() $T$ denote a split maximal torus and choose a set of positive roots
$T$ denote a split maximal torus and choose a set of positive roots ![]() $\Phi _G^+$. Let
$\Phi _G^+$. Let ![]() $\mu \in X_*(T)$ be a dominant cocharacter. We let
$\mu \in X_*(T)$ be a dominant cocharacter. We let ![]() $\operatorname {LG}$ and
$\operatorname {LG}$ and ![]() $\textrm {L}^+G$ denote the loop group and the positive loop group for
$\textrm {L}^+G$ denote the loop group and the positive loop group for ![]() $G$, respectively, over
$G$, respectively, over ![]() $k$. The affine Grassmanian
$k$. The affine Grassmanian ![]() $\operatorname {Gr}_G$ is the quotient
$\operatorname {Gr}_G$ is the quotient ![]() $\textrm {L}^+G \backslash \operatorname {LG}$. As before, the affine Schubert cell
$\textrm {L}^+G \backslash \operatorname {LG}$. As before, the affine Schubert cell ![]() $\operatorname {Gr}^{\circ, \mu }_{G}$ is the reduced
$\operatorname {Gr}^{\circ, \mu }_{G}$ is the reduced ![]() $\textrm {L}^+G$-orbit of
$\textrm {L}^+G$-orbit of ![]() $u^{\mu }$, and
$u^{\mu }$, and ![]() $\operatorname {Gr}^{\leqslant \mu }_{G}$ its closure.
$\operatorname {Gr}^{\leqslant \mu }_{G}$ its closure.
5.1 Tangent spaces
Let ![]() $\mu '$ be a dominant cocharacter such that
$\mu '$ be a dominant cocharacter such that ![]() $\mu ' \leqslant \mu$. For the key calculations in the next section, we need some basic control over the tangent space of
$\mu ' \leqslant \mu$. For the key calculations in the next section, we need some basic control over the tangent space of ![]() $\operatorname {Gr}_{G}^{\leqslant \mu }$ at the
$\operatorname {Gr}_{G}^{\leqslant \mu }$ at the ![]() $T$-fixed point
$T$-fixed point ![]() $[u^{\mu '}]$. We use the subgroup ind-scheme
$[u^{\mu '}]$. We use the subgroup ind-scheme ![]() $L^{--} G \subset LG$ given by
$L^{--} G \subset LG$ given by
for any ![]() $k$-algebra
$k$-algebra ![]() $A$. Recall that the natural map
$A$. Recall that the natural map ![]() $L^{--} G \rightarrow \operatorname {Gr}_{G}$ is representable by an open immersion (see, for example, [Reference Haines and RicharzHR21, Lemma 3.1]). Thus, we can identify the tangent space at the base point
$L^{--} G \rightarrow \operatorname {Gr}_{G}$ is representable by an open immersion (see, for example, [Reference Haines and RicharzHR21, Lemma 3.1]). Thus, we can identify the tangent space at the base point ![]() $e$ of
$e$ of ![]() $\operatorname {Gr}_{G}$ with
$\operatorname {Gr}_{G}$ with ![]() $\operatorname {Lie} L^{--} G = u^{-1} (\mathfrak {g}_{k[u^{-1}]}) \subset \mathfrak {g}_{ k(\!(u)\!)}$. Recall that we defined
$\operatorname {Lie} L^{--} G = u^{-1} (\mathfrak {g}_{k[u^{-1}]}) \subset \mathfrak {g}_{ k(\!(u)\!)}$. Recall that we defined
Proposition 5.1.1 Assume that ![]() $Z^{\mathrm {der}}$ is étale over
$Z^{\mathrm {der}}$ is étale over ![]() $k$. Let
$k$. Let ![]() $\mu$ and
$\mu$ and ![]() $\mu '$ be dominant coweights such that
$\mu '$ be dominant coweights such that ![]() $\mu ' \leqslant \mu$. The tangent space to
$\mu ' \leqslant \mu$. The tangent space to ![]() $(\operatorname {Gr}_{G}^{\leqslant \mu }) u^{-\mu '}$ at
$(\operatorname {Gr}_{G}^{\leqslant \mu }) u^{-\mu '}$ at ![]() $e$ is contained in the subspace
$e$ is contained in the subspace ![]() $V^{\mu }_{\mu '}$ generated as a
$V^{\mu }_{\mu '}$ generated as a ![]() $k$-vector space by the following subspaces of
$k$-vector space by the following subspaces of ![]() $\operatorname {Lie} L^{--} G$:
$\operatorname {Lie} L^{--} G$:
– for
 $\alpha \in \Phi _G$ and
$\alpha \in \Phi _G$ and  $1 \leqslant j \leqslant \frac {1}{2}(h_{\mu } - \langle \mu ', \alpha \rangle )$, the subspaces
$1 \leqslant j \leqslant \frac {1}{2}(h_{\mu } - \langle \mu ', \alpha \rangle )$, the subspaces  $u^{-j} \mathfrak {g}_{\alpha }$; and
$u^{-j} \mathfrak {g}_{\alpha }$; and– for
 $1 \leqslant j \leqslant h_{\mu }$, the subspaces
$1 \leqslant j \leqslant h_{\mu }$, the subspaces  $u^{-j} (\operatorname {Lie} T)$.
$u^{-j} (\operatorname {Lie} T)$.
Proof. For any ![]() $\alpha \in \Phi _G$, we have the corresponding root group
$\alpha \in \Phi _G$, we have the corresponding root group ![]() $U_{\alpha } \subset G$, which is a copy of
$U_{\alpha } \subset G$, which is a copy of ![]() $\mathbf {G}_a$. For any integer
$\mathbf {G}_a$. For any integer ![]() $n$,
$n$, ![]() $U_{\alpha } (t u^n) \subset L G$ is an affine root group with coordinate
$U_{\alpha } (t u^n) \subset L G$ is an affine root group with coordinate ![]() $t$. For
$t$. For ![]() $j \geqslant 1$, the tangent space to
$j \geqslant 1$, the tangent space to ![]() $U_{\alpha }(t u^{-j})$ is
$U_{\alpha }(t u^{-j})$ is ![]() $u^{-j} \mathfrak {g}_{\alpha }$.
$u^{-j} \mathfrak {g}_{\alpha }$.
To bound the tangent space, we use the adjoint representation denoted ![]() $\mathrm {Ad}$. The map
$\mathrm {Ad}$. The map ![]() $\operatorname {Ad}:G \rightarrow \operatorname {GL}(\operatorname {Lie} G)$ induces a map of affine Grassmannians
$\operatorname {Ad}:G \rightarrow \operatorname {GL}(\operatorname {Lie} G)$ induces a map of affine Grassmannians ![]() $\operatorname {Ad}_* :\operatorname {Gr}_{G} \rightarrow \operatorname {Gr}_{\operatorname {GL}(\operatorname {Lie} G)}$. There is a closed subscheme
$\operatorname {Ad}_* :\operatorname {Gr}_{G} \rightarrow \operatorname {Gr}_{\operatorname {GL}(\operatorname {Lie} G)}$. There is a closed subscheme ![]() $\operatorname {Gr}^{[-h_{\mu }, h_{\mu }]}_{\operatorname {GL}(\operatorname {Lie} G)}$ which is the image of the subfunctor
$\operatorname {Gr}^{[-h_{\mu }, h_{\mu }]}_{\operatorname {GL}(\operatorname {Lie} G)}$ which is the image of the subfunctor ![]() $\{ g \in \textrm {L} {\operatorname {GL}(\operatorname {Lie} G)}(A) \mid u^{h_{\mu }} g, u^{h_{\mu }} g^{-1} \in \operatorname {End}(\operatorname {Lie} G)(A[\![u]\!]) \}$. This subfunctor is clearly closed under right multiplication by
$\{ g \in \textrm {L} {\operatorname {GL}(\operatorname {Lie} G)}(A) \mid u^{h_{\mu }} g, u^{h_{\mu }} g^{-1} \in \operatorname {End}(\operatorname {Lie} G)(A[\![u]\!]) \}$. This subfunctor is clearly closed under right multiplication by ![]() $\textrm {L}^+ {\operatorname {GL}(\operatorname {Lie} G)}$. Since
$\textrm {L}^+ {\operatorname {GL}(\operatorname {Lie} G)}$. Since ![]() $\operatorname {Ad}_*(u^{\mu }) \in \operatorname {Gr}^{[-h_{\mu }, h_{\mu }]}_{\operatorname {GL}(\operatorname {Lie} G)}$, it follows that
$\operatorname {Ad}_*(u^{\mu }) \in \operatorname {Gr}^{[-h_{\mu }, h_{\mu }]}_{\operatorname {GL}(\operatorname {Lie} G)}$, it follows that
Assuming that ![]() $U_{\alpha }(tu^{-j})$ lies in
$U_{\alpha }(tu^{-j})$ lies in ![]() $( \operatorname {Gr}^{\leqslant \mu }_G) u^{-\mu '}$, then
$( \operatorname {Gr}^{\leqslant \mu }_G) u^{-\mu '}$, then ![]() $\operatorname {Ad}_{*}(U_{\alpha }(tu^{-j})) \operatorname {Ad}_{*}(u^{\mu '})$ lies in
$\operatorname {Ad}_{*}(U_{\alpha }(tu^{-j})) \operatorname {Ad}_{*}(u^{\mu '})$ lies in ![]() $\operatorname {Gr}^{[-h_{\mu }, h_{\mu }]}_{\operatorname {GL}(\operatorname {Lie} G)}$ and so satisfies the height condition. Let
$\operatorname {Gr}^{[-h_{\mu }, h_{\mu }]}_{\operatorname {GL}(\operatorname {Lie} G)}$ and so satisfies the height condition. Let ![]() $e_{-\alpha }$ and
$e_{-\alpha }$ and ![]() $e_{\alpha }$ generate
$e_{\alpha }$ generate ![]() $\mathfrak {g}_{-\alpha }$ and
$\mathfrak {g}_{-\alpha }$ and ![]() $\mathfrak {g}_{\alpha }$, respectively, in
$\mathfrak {g}_{\alpha }$, respectively, in ![]() $\operatorname {Lie} G$. The height condition defining
$\operatorname {Lie} G$. The height condition defining ![]() $\operatorname {Gr}^{[-h_{\mu }, h_{\mu }]}_{\operatorname {GL}(\operatorname {Lie} G)}$ implies that
$\operatorname {Gr}^{[-h_{\mu }, h_{\mu }]}_{\operatorname {GL}(\operatorname {Lie} G)}$ implies that
A straightforward computation, for example using the map ![]() $\mathrm {SL}_2 \rightarrow G$ sending the upper triangular
$\mathrm {SL}_2 \rightarrow G$ sending the upper triangular ![]() $\mathbf {G}_a$ to
$\mathbf {G}_a$ to ![]() $U_{\alpha }$, shows that the coefficient on
$U_{\alpha }$, shows that the coefficient on ![]() $e_{\alpha }$ of
$e_{\alpha }$ of ![]() $\operatorname {Ad}(U_{\alpha }(tu^{-j})) \operatorname {Ad}(u^{\mu '}) (e_{-\alpha })$ is a scalar multiple of
$\operatorname {Ad}(U_{\alpha }(tu^{-j})) \operatorname {Ad}(u^{\mu '}) (e_{-\alpha })$ is a scalar multiple of ![]() $-t^2 u^{-2j - \langle \mu ',\alpha \rangle }$. Thus, (5.1.1) implies that
$-t^2 u^{-2j - \langle \mu ',\alpha \rangle }$. Thus, (5.1.1) implies that
which implies the first item.
We now explain how to reduce checking the second item to the adjoint case. Let ![]() $G^{\mathrm {der}}, G^{\mathrm {ad}}$ denote the derived and adjoint groups of
$G^{\mathrm {der}}, G^{\mathrm {ad}}$ denote the derived and adjoint groups of ![]() $G$, respectively. By § 6.a.1 of [Reference Pappas and RapoportPR08],
$G$, respectively. By § 6.a.1 of [Reference Pappas and RapoportPR08], ![]() $\operatorname {Gr}_{G^{\mathrm {der}}} \rightarrow \operatorname {Gr}_{G^{\mathrm {ad}}}$ is a closed immersion. Furthermore, by Proposition 6.6 in [Reference Pappas and RapoportPR08], the reduced connected component of
$\operatorname {Gr}_{G^{\mathrm {der}}} \rightarrow \operatorname {Gr}_{G^{\mathrm {ad}}}$ is a closed immersion. Furthermore, by Proposition 6.6 in [Reference Pappas and RapoportPR08], the reduced connected component of ![]() $\operatorname {Gr}_G$ containing the base point is identified with the same for
$\operatorname {Gr}_G$ containing the base point is identified with the same for ![]() $\operatorname {Gr}_ {G^{\mathrm {der}}}$. Thus,
$\operatorname {Gr}_ {G^{\mathrm {der}}}$. Thus, ![]() $\operatorname {Gr}_G^{\leqslant \mu } u^{-\mu '} \subset \operatorname {Gr}_ {G^{\mathrm {der}}}$. It is clear then that if we let
$\operatorname {Gr}_G^{\leqslant \mu } u^{-\mu '} \subset \operatorname {Gr}_ {G^{\mathrm {der}}}$. It is clear then that if we let ![]() $\overline {\mu }, \overline {\mu }'$ denote the image of
$\overline {\mu }, \overline {\mu }'$ denote the image of ![]() $\mu$ and
$\mu$ and ![]() $\mu '$ in the
$\mu '$ in the ![]() $X_*(T^{\mathrm {ad}})$, then
$X_*(T^{\mathrm {ad}})$, then
Thereby, we may reduce to the case when ![]() $G$ is adjoint to analyze the torus contribution.
$G$ is adjoint to analyze the torus contribution.
Let ![]() $Y \in \operatorname {Lie} T$, and assume
$Y \in \operatorname {Lie} T$, and assume ![]() $u^{-j} Y$ lies in the tangent space to
$u^{-j} Y$ lies in the tangent space to ![]() $(\operatorname {Gr}_G^{\leqslant \mu }) u^{-\mu '}$. By the adjointness assumption, there exists some
$(\operatorname {Gr}_G^{\leqslant \mu }) u^{-\mu '}$. By the adjointness assumption, there exists some ![]() $\alpha \in \Phi _G^+$ such that
$\alpha \in \Phi _G^+$ such that ![]() $\alpha (Y) \neq 0$. By the same argument as before, considering
$\alpha (Y) \neq 0$. By the same argument as before, considering ![]() $\operatorname {Ad}(u^{-j}Y) \operatorname {Ad}(u^{\mu '}) e_{-\alpha }$ gives that
$\operatorname {Ad}(u^{-j}Y) \operatorname {Ad}(u^{\mu '}) e_{-\alpha }$ gives that
Remark 5.1.2 There is a formula for the tangent space to ![]() $\operatorname {Gr}_{G}^{\leqslant \mu }$ at
$\operatorname {Gr}_{G}^{\leqslant \mu }$ at ![]() $[ u^{-\mu '} ]$ in terms of affine Demazure modules in characteristic 0 due to Kumar [Reference KumarKum96] for Kac–Moody groups. It is unclear to us whether this formula holds in characteristic
$[ u^{-\mu '} ]$ in terms of affine Demazure modules in characteristic 0 due to Kumar [Reference KumarKum96] for Kac–Moody groups. It is unclear to us whether this formula holds in characteristic ![]() $p$ and so we opted to prove the upper bound directly.
$p$ and so we opted to prove the upper bound directly.
Remark 5.1.3 If ![]() $k$ has characteristic
$k$ has characteristic ![]() $p$ and
$p$ and ![]() $G = \operatorname {GL}_n$ the hypothesis that
$G = \operatorname {GL}_n$ the hypothesis that ![]() $p \nmid n$ (so
$p \nmid n$ (so ![]() $Z^{\operatorname {der}} = \mu _n$ is étale) is not needed. We can argue directly, without reducing to checking the second item for adjoint case, by considering the action of
$Z^{\operatorname {der}} = \mu _n$ is étale) is not needed. We can argue directly, without reducing to checking the second item for adjoint case, by considering the action of ![]() $T$ on the standard representation. The key is the elementary observation that if
$T$ on the standard representation. The key is the elementary observation that if ![]() $\mu$ is the cocharacter given by the
$\mu$ is the cocharacter given by the ![]() $n$-tuple of integers
$n$-tuple of integers ![]() $(a_1,\ldots, a_n)$, then the standard representation has height in
$(a_1,\ldots, a_n)$, then the standard representation has height in ![]() $[\min _i a_i, \max _i a_i]$, while
$[\min _i a_i, \max _i a_i]$, while ![]() $h_\mu = \max _i a_i - \min _i a_i$.
$h_\mu = \max _i a_i - \min _i a_i$.
5.2 Monodromy locus
Recall that for any ![]() $k$-algebra
$k$-algebra ![]() $A$ and any
$A$ and any ![]() $C \in \operatorname {LG}(A)$, we defined an element
$C \in \operatorname {LG}(A)$, we defined an element ![]() $ ({dC}/{du}) C^{-1} \in \operatorname {Lie} \operatorname {LG} (A)$ characterized using the Tannakian formalism in Definition 4.1.13. Define a closed subfunctor
$ ({dC}/{du}) C^{-1} \in \operatorname {Lie} \operatorname {LG} (A)$ characterized using the Tannakian formalism in Definition 4.1.13. Define a closed subfunctor
Remark 4.1.14 shows that ![]() $LG^{\nabla }$ is stable under left multiplication by
$LG^{\nabla }$ is stable under left multiplication by ![]() $\textrm {L}^+G$, so we can define closed sub-(ind)-schemes
$\textrm {L}^+G$, so we can define closed sub-(ind)-schemes
We can now state the main theorem of the section.
Theorem 5.2.1 Let ![]() $\mu \in X_*(T)$ be a dominant coweight. If
$\mu \in X_*(T)$ be a dominant coweight. If ![]() $k$ has finite characteristic
$k$ has finite characteristic ![]() $p$, then assume that
$p$, then assume that ![]() $\langle \mu, \alpha \rangle < p$ for all positive roots
$\langle \mu, \alpha \rangle < p$ for all positive roots ![]() $\alpha$ and that
$\alpha$ and that ![]() $Z^{\operatorname {der}}$ is étale over
$Z^{\operatorname {der}}$ is étale over ![]() $k$. Then we have that
$k$. Then we have that
where ![]() $P_{\mu '}$ is the parabolic subgroup associated to
$P_{\mu '}$ is the parabolic subgroup associated to ![]() $\mu '$. In particular,
$\mu '$. In particular, ![]() $\operatorname {Gr}_{G}^{\leqslant \mu, \nabla }$ is smooth.
$\operatorname {Gr}_{G}^{\leqslant \mu, \nabla }$ is smooth.
Remark 5.2.2 The strategy is similar to the approach taken in [Reference Le, Le Hung, Levin and MorraLLHLM23, §§ 3–4] where an analogous fact is proven for ![]() $\operatorname {GL}_n$.
$\operatorname {GL}_n$.
The proof will reduce to the following key computation on tangent spaces.
Proposition 5.2.3 If ![]() $k$ has finite characteristic
$k$ has finite characteristic ![]() $p$, assume that
$p$, assume that ![]() $h_{\mu } < p$ and that
$h_{\mu } < p$ and that ![]() $Z^{\operatorname {der}}$ is étale over
$Z^{\operatorname {der}}$ is étale over ![]() $k$. For a dominant
$k$. For a dominant ![]() $\mu ' \leqslant \mu$, the dimension of the tangent space of
$\mu ' \leqslant \mu$, the dimension of the tangent space of ![]() $\operatorname {Gr}_{G}^{\leqslant \mu, \nabla }$ at
$\operatorname {Gr}_{G}^{\leqslant \mu, \nabla }$ at ![]() $[u^{\mu '}]$ is equal to
$[u^{\mu '}]$ is equal to ![]() $\dim P_{\mu '} \backslash G$.
$\dim P_{\mu '} \backslash G$.
Proof. As in Proposition 5.1.1, we translate and consider the tangent space ![]() $W^{\mu }_{\mu '}$ of
$W^{\mu }_{\mu '}$ of ![]() $(\operatorname {Gr}_{G}^{\leqslant \mu }) u^{-\mu '}$ at the base point
$(\operatorname {Gr}_{G}^{\leqslant \mu }) u^{-\mu '}$ at the base point ![]() $e$ as a subspace of
$e$ as a subspace of ![]() $\operatorname {Lie} L^{--} G$. By [Reference Le, Le Hung, Levin and MorraLLHLM23],
$\operatorname {Lie} L^{--} G$. By [Reference Le, Le Hung, Levin and MorraLLHLM23], ![]() $W^{\mu }_{\mu '} \subset V^{\mu }_{\mu '}$. Since
$W^{\mu }_{\mu '} \subset V^{\mu }_{\mu '}$. Since ![]() $\operatorname {Gr}^{\circ,\mu '}_{G} \subset \operatorname {Gr}_{G}^{\leqslant \mu }$, Lemma 2.3.3 gives that
$\operatorname {Gr}^{\circ,\mu '}_{G} \subset \operatorname {Gr}_{G}^{\leqslant \mu }$, Lemma 2.3.3 gives that ![]() $V_{\mu '} \subset W^{\mu }_{\mu '}$.
$V_{\mu '} \subset W^{\mu }_{\mu '}$.
It is elementary to check that ![]() $u^{\mu '} \in \operatorname {LG}^{\nabla }$ and so
$u^{\mu '} \in \operatorname {LG}^{\nabla }$ and so ![]() $[u^{\mu '}] \in \operatorname {Gr}_{G}^{\leqslant \mu, \nabla }$. Let
$[u^{\mu '}] \in \operatorname {Gr}_{G}^{\leqslant \mu, \nabla }$. Let ![]() $V_{\mu '}^{\nabla }$ and
$V_{\mu '}^{\nabla }$ and ![]() $W^{\mu, \nabla }_{\mu '}$ denote the tangent spaces to
$W^{\mu, \nabla }_{\mu '}$ denote the tangent spaces to ![]() $(\operatorname {Gr}_{G}^{\circ,\mu '} \cap \operatorname {Gr}_G^{\nabla }) u^{-\mu '}$ and
$(\operatorname {Gr}_{G}^{\circ,\mu '} \cap \operatorname {Gr}_G^{\nabla }) u^{-\mu '}$ and ![]() $(\operatorname {Gr}^{\leqslant \mu, \nabla }_{G}) u^{-\mu '}$, respectively, at the identity. For
$(\operatorname {Gr}^{\leqslant \mu, \nabla }_{G}) u^{-\mu '}$, respectively, at the identity. For ![]() $Y \in W^{\mu }_{\mu '}$ that translates to
$Y \in W^{\mu }_{\mu '}$ that translates to ![]() $C \in \operatorname {LG}(k[\epsilon ]/(\epsilon )^2)$, the key observation is that
$C \in \operatorname {LG}(k[\epsilon ]/(\epsilon )^2)$, the key observation is that ![]() $Y \in W^{\mu, \nabla }_{\mu '}$ if and only if
$Y \in W^{\mu, \nabla }_{\mu '}$ if and only if
This can be checked using any faithful representation ![]() $V$ of
$V$ of ![]() $G$, where we compute that
$G$, where we compute that ![]() $[C]_V= ([1]_V + \epsilon [Y]_V )u^{\mu '}$ and, hence,
$[C]_V= ([1]_V + \epsilon [Y]_V )u^{\mu '}$ and, hence,
 \begin{align*} \frac{d[C]_V}{du} [C]_V^{-1} &= \frac{d\big( ([1]_V + \epsilon [Y]_V )u^{\mu'} \big)}{du} u^{-\mu'}([1]_V - \epsilon [Y]_V ) \\ &= \frac{d u^{\mu'}}{du} u^{-\mu'} [1]_V + \epsilon \bigg( \frac{d[Y]_V}{du} + [Y]_V \frac{du^{\mu'}}{du} u^{-\mu'} - \frac{d u^{\mu'}}{du} u^{-\mu'} [Y]_V \bigg). \end{align*}
\begin{align*} \frac{d[C]_V}{du} [C]_V^{-1} &= \frac{d\big( ([1]_V + \epsilon [Y]_V )u^{\mu'} \big)}{du} u^{-\mu'}([1]_V - \epsilon [Y]_V ) \\ &= \frac{d u^{\mu'}}{du} u^{-\mu'} [1]_V + \epsilon \bigg( \frac{d[Y]_V}{du} + [Y]_V \frac{du^{\mu'}}{du} u^{-\mu'} - \frac{d u^{\mu'}}{du} u^{-\mu'} [Y]_V \bigg). \end{align*}
We see this is in ![]() $ ({1}/{u}) \operatorname {Lie} \textrm {L}^+G(k[\epsilon ]/(\epsilon ^2))$ precisely when
$ ({1}/{u}) \operatorname {Lie} \textrm {L}^+G(k[\epsilon ]/(\epsilon ^2))$ precisely when ![]() $u ({d[Y]_V}/{du}) + [ [Y]_V,\mu '] \in \mathfrak {g}_{k[\![u ] \!]}$.
$u ({d[Y]_V}/{du}) + [ [Y]_V,\mu '] \in \mathfrak {g}_{k[\![u ] \!]}$.
We first analyze ![]() $V_{\mu '}^{\nabla }$. Using Lemma 2.3.3, for any
$V_{\mu '}^{\nabla }$. Using Lemma 2.3.3, for any ![]() $\alpha$ such that
$\alpha$ such that ![]() $\langle \mu ', \alpha \rangle < 0$ we can represent the
$\langle \mu ', \alpha \rangle < 0$ we can represent the ![]() $\alpha$-component of
$\alpha$-component of ![]() $Y$ as
$Y$ as ![]() $Y_{\alpha } = \sum _{i=-1}^{\langle \mu ', \alpha \rangle } Y_{\alpha, i} u^{i}$ where
$Y_{\alpha } = \sum _{i=-1}^{\langle \mu ', \alpha \rangle } Y_{\alpha, i} u^{i}$ where ![]() $Y_{\alpha, i} \in k$. Then condition (5.2.2) becomes
$Y_{\alpha, i} \in k$. Then condition (5.2.2) becomes
 \[ \sum_{i=-1}^{\langle \mu', \alpha \rangle} (i - \langle \mu', \alpha \rangle ) Y_{\alpha, i} u^{i} \in k[\![u]\!]. \]
\[ \sum_{i=-1}^{\langle \mu', \alpha \rangle} (i - \langle \mu', \alpha \rangle ) Y_{\alpha, i} u^{i} \in k[\![u]\!]. \]
Since ![]() $-p < \langle \mu ', \alpha \rangle < 0$, we see
$-p < \langle \mu ', \alpha \rangle < 0$, we see ![]() $(i - \langle \mu ', \alpha \rangle ) \neq 0$ in
$(i - \langle \mu ', \alpha \rangle ) \neq 0$ in ![]() $k$ for
$k$ for ![]() $\langle \mu ', \alpha \rangle < i < 0$ and, hence,
$\langle \mu ', \alpha \rangle < i < 0$ and, hence, ![]() $Y_{\alpha,i}=0$. There is no restriction on
$Y_{\alpha,i}=0$. There is no restriction on ![]() $Y_{\alpha, \langle \mu ',\alpha \rangle }$. Since
$Y_{\alpha, \langle \mu ',\alpha \rangle }$. Since ![]() $\dim P_{\mu '} \backslash G$ is equal to the number of positive roots such that
$\dim P_{\mu '} \backslash G$ is equal to the number of positive roots such that ![]() $\langle \mu ', \alpha \rangle > 0$, we have
$\langle \mu ', \alpha \rangle > 0$, we have ![]() $\dim V_{\mu '}^{\nabla } = \dim P_{\mu '} \backslash G$ and, hence,
$\dim V_{\mu '}^{\nabla } = \dim P_{\mu '} \backslash G$ and, hence,
Define ![]() $V_{\mu '}^{\mu, \nabla }$ to be the subspace of
$V_{\mu '}^{\mu, \nabla }$ to be the subspace of ![]() $V^{\mu }_{\mu '}$ satisfying (5.2.2), and let
$V^{\mu }_{\mu '}$ satisfying (5.2.2), and let ![]() $Y \in V^{\mu }_{\mu '}$. As before, we can write the
$Y \in V^{\mu }_{\mu '}$. As before, we can write the ![]() $\alpha$-component of
$\alpha$-component of ![]() $Y$ as
$Y$ as ![]() $Y_{\alpha } = \sum _{i=-1}^{-N} Y_{\alpha, i} u^{i}$ with
$Y_{\alpha } = \sum _{i=-1}^{-N} Y_{\alpha, i} u^{i}$ with ![]() $Y_{\alpha, i} \in k$ where
$Y_{\alpha, i} \in k$ where ![]() $N := \frac {1}{2}(h_{\mu } - \langle \mu ', \alpha \rangle )$ is the bound given in Proposition 5.1.1. Again, we must have
$N := \frac {1}{2}(h_{\mu } - \langle \mu ', \alpha \rangle )$ is the bound given in Proposition 5.1.1. Again, we must have
 \[ \sum_{i=-1}^{-N} (i - \langle \mu', \alpha \rangle ) Y_{\alpha, i} u^{i} \in k[\![u]\!]. \]
\[ \sum_{i=-1}^{-N} (i - \langle \mu', \alpha \rangle ) Y_{\alpha, i} u^{i} \in k[\![u]\!]. \]
Note that for ![]() $-N \leqslant i \leqslant -1$, we have
$-N \leqslant i \leqslant -1$, we have ![]() $-1 - \langle \mu ', \alpha \rangle \geqslant i - \langle \mu ', \alpha \rangle \geqslant - \frac {1}{2} (h_{\mu } + \langle \mu ', \alpha \rangle )$. For
$-1 - \langle \mu ', \alpha \rangle \geqslant i - \langle \mu ', \alpha \rangle \geqslant - \frac {1}{2} (h_{\mu } + \langle \mu ', \alpha \rangle )$. For ![]() $\alpha \in \Phi _G^+$, since
$\alpha \in \Phi _G^+$, since ![]() $\mu ' \leqslant \mu$ we see that
$\mu ' \leqslant \mu$ we see that ![]() $\langle \mu ', \alpha \rangle \leqslant h_{\mu }$. Hence,
$\langle \mu ', \alpha \rangle \leqslant h_{\mu }$. Hence, ![]() $i - \langle \mu ', \alpha \rangle > -p$ and, thus,
$i - \langle \mu ', \alpha \rangle > -p$ and, thus, ![]() $Y_{\alpha,i} =0$. If
$Y_{\alpha,i} =0$. If ![]() $\alpha \in \Phi _G^-$, a similar check confirms that
$\alpha \in \Phi _G^-$, a similar check confirms that ![]() $(i - \langle \mu ', \alpha \rangle ) \equiv 0 \mod p$ only if
$(i - \langle \mu ', \alpha \rangle ) \equiv 0 \mod p$ only if ![]() $i = \langle \mu ', \alpha \rangle$. Hence
$i = \langle \mu ', \alpha \rangle$. Hence ![]() $Y_{\alpha,i}=0$ except if
$Y_{\alpha,i}=0$ except if ![]() $i = \langle \mu ', \alpha \rangle$ and
$i = \langle \mu ', \alpha \rangle$ and ![]() $\langle \mu ', \alpha \rangle \neq 0$.
$\langle \mu ', \alpha \rangle \neq 0$.
Finally, consider ![]() $Y \in V^{\mu }_{\mu '} \cap \mathfrak {t}_{k(\!(u)\!)}$. By Proposition 5.1.1,
$Y \in V^{\mu }_{\mu '} \cap \mathfrak {t}_{k(\!(u)\!)}$. By Proposition 5.1.1, ![]() $Y = \sum _{i=1}^{h_{\mu }} Y_i u^{-i}$ where
$Y = \sum _{i=1}^{h_{\mu }} Y_i u^{-i}$ where ![]() $Y_i \in \mathfrak {t}$. Condition (5.2.2) becomes
$Y_i \in \mathfrak {t}$. Condition (5.2.2) becomes
 \[ \sum_{i=1}^{h_{\mu}} ( -i Y_i) u^{-i} \in \mathfrak{t}_{ k[\![u]\!]}. \]
\[ \sum_{i=1}^{h_{\mu}} ( -i Y_i) u^{-i} \in \mathfrak{t}_{ k[\![u]\!]}. \]
Since ![]() $h_{\mu } < p$, this implies that each
$h_{\mu } < p$, this implies that each ![]() $Y_i = 0$.
$Y_i = 0$.
Since ![]() $\dim P_{\mu '} \backslash G$ equals the number of positive roots such that
$\dim P_{\mu '} \backslash G$ equals the number of positive roots such that ![]() $\langle \mu ',\alpha \rangle >0$, we conclude that
$\langle \mu ',\alpha \rangle >0$, we conclude that ![]() $\dim W^{\mu,\nabla }_{\mu '} \leqslant \dim V_{\mu '}^{\mu, \nabla } \leqslant \dim P_{\mu '} \backslash G$. Together with (5.2.3) this completes the proof.
$\dim W^{\mu,\nabla }_{\mu '} \leqslant \dim V_{\mu '}^{\mu, \nabla } \leqslant \dim P_{\mu '} \backslash G$. Together with (5.2.3) this completes the proof.
Letting ![]() $e_\alpha$ generate
$e_\alpha$ generate ![]() $\mathfrak {g}_\alpha$, the previous proof also shows.
$\mathfrak {g}_\alpha$, the previous proof also shows.
Corollary 5.2.4 With hypotheses as in Proposition 5.2.3, using the map on tangent spaces induced by right translation by ![]() $u^{\mu '}$, the tangent space of
$u^{\mu '}$, the tangent space of ![]() $\operatorname {Gr}_{G}^{\leqslant \mu, \nabla }$ at
$\operatorname {Gr}_{G}^{\leqslant \mu, \nabla }$ at ![]() $u^{\mu '}$ is contained in
$u^{\mu '}$ is contained in
We now consider the open affine Schubert cell ![]() $\operatorname {Gr}_{G}^{\circ,\mu '}$ and its intersection with
$\operatorname {Gr}_{G}^{\circ,\mu '}$ and its intersection with ![]() $\operatorname {Gr}_G^{\nabla }$ for any dominant cocharacter
$\operatorname {Gr}_G^{\nabla }$ for any dominant cocharacter ![]() $\mu '$. We show that
$\mu '$. We show that ![]() $\operatorname {Gr}_{G}^{\circ, \mu ', \nabla } := \operatorname {Gr}_{G}^{\circ,\mu '} \cap \operatorname {Gr}_G^{\nabla }$ is equal to the orbit
$\operatorname {Gr}_{G}^{\circ, \mu ', \nabla } := \operatorname {Gr}_{G}^{\circ,\mu '} \cap \operatorname {Gr}_G^{\nabla }$ is equal to the orbit ![]() $u^{\mu '} G$; this is known to be a flag variety.
$u^{\mu '} G$; this is known to be a flag variety.
Proposition 5.2.5 Let ![]() $\mu ' \in X_*(T)$ be a dominant coweight. If
$\mu ' \in X_*(T)$ be a dominant coweight. If ![]() $k$ has finite characteristic
$k$ has finite characteristic ![]() $p$, then assume that
$p$, then assume that ![]() $\langle \mu ', \alpha \rangle < p$ for all positive roots
$\langle \mu ', \alpha \rangle < p$ for all positive roots ![]() $\alpha \in \Phi _G^+$ and that
$\alpha \in \Phi _G^+$ and that ![]() $Z^{\operatorname {der}}$ is étale over
$Z^{\operatorname {der}}$ is étale over ![]() $k$. Then we have
$k$. Then we have
Proof. We first show that the closed subscheme ![]() $\operatorname {Gr}_{G}^{\circ,\mu ', \nabla } \subset \operatorname {Gr}_{G}^{\circ, \mu '}$ is stable under the right multiplication by
$\operatorname {Gr}_{G}^{\circ,\mu ', \nabla } \subset \operatorname {Gr}_{G}^{\circ, \mu '}$ is stable under the right multiplication by ![]() $G$. It suffices to show that
$G$. It suffices to show that ![]() $\operatorname {LG}^{\nabla }$ is stable under right multiplication by
$\operatorname {LG}^{\nabla }$ is stable under right multiplication by ![]() $G$. Let
$G$. Let ![]() $A$ be a
$A$ be a ![]() $k$-algebra. For any
$k$-algebra. For any ![]() $C \in LG^{\nabla }(A)$ and
$C \in LG^{\nabla }(A)$ and ![]() $g \in G(A)$, by Remark 4.1.14
$g \in G(A)$, by Remark 4.1.14
As ![]() $g \in G(A)$,
$g \in G(A)$, ![]() $ ({dg}/{du}) g^{-1} = 0$ and, hence,
$ ({dg}/{du}) g^{-1} = 0$ and, hence, ![]() $Cg \in LG^{\nabla }(A)$.
$Cg \in LG^{\nabla }(A)$.
Next, let ![]() $X_{\mu '} \subset \operatorname {Gr}_{G}^{\circ,\mu '}$ denote the orbit
$X_{\mu '} \subset \operatorname {Gr}_{G}^{\circ,\mu '}$ denote the orbit ![]() $u^{\mu '} G$. It is well known that
$u^{\mu '} G$. It is well known that ![]() $X_{\mu '} \cong P_{\mu '} \backslash G$ and, hence, is projective (see top of p. 100 of [Reference Mirković and VilonenMV07]). Now note that
$X_{\mu '} \cong P_{\mu '} \backslash G$ and, hence, is projective (see top of p. 100 of [Reference Mirković and VilonenMV07]). Now note that ![]() $X_{\mu '} \subset \operatorname {Gr}_{G}^{\circ,\mu ', \nabla }$ since
$X_{\mu '} \subset \operatorname {Gr}_{G}^{\circ,\mu ', \nabla }$ since ![]() $u^{\mu '} \in LG^{\nabla }(k)$. Furthermore, we claim that the inclusion
$u^{\mu '} \in LG^{\nabla }(k)$. Furthermore, we claim that the inclusion ![]() $X_{\mu '} \subset \operatorname {Gr}_{G}^{\circ,\mu ', \nabla }$ is an open immersion and, thus, (the projective)
$X_{\mu '} \subset \operatorname {Gr}_{G}^{\circ,\mu ', \nabla }$ is an open immersion and, thus, (the projective) ![]() $X_{\mu '}$ is a connected component of
$X_{\mu '}$ is a connected component of ![]() $\operatorname {Gr}_{G}^{\circ, \mu ',\nabla }$. Since the inclusion is
$\operatorname {Gr}_{G}^{\circ, \mu ',\nabla }$. Since the inclusion is ![]() $G$-equivariant and
$G$-equivariant and ![]() $G$ acts transitively on
$G$ acts transitively on ![]() $X_{\mu '}$, it suffices to show that map on tangent spaces at
$X_{\mu '}$, it suffices to show that map on tangent spaces at ![]() $u^{\mu '}$ is an isomorphism. This follows from proof of Proposition 5.2.3 which shows that the dimension of the tangent space of
$u^{\mu '}$ is an isomorphism. This follows from proof of Proposition 5.2.3 which shows that the dimension of the tangent space of ![]() $\operatorname {Gr}_{G}^{\circ,\mu ', \nabla }$ at
$\operatorname {Gr}_{G}^{\circ,\mu ', \nabla }$ at ![]() $u^{\mu '}$ is equal to
$u^{\mu '}$ is equal to ![]() $\dim P_{\mu '} \backslash G$.
$\dim P_{\mu '} \backslash G$.
Finally, recall the loop ![]() $\mathbf {G}_m$ action on
$\mathbf {G}_m$ action on ![]() $\operatorname {Gr}_G$ denoted
$\operatorname {Gr}_G$ denoted ![]() $\check {\delta }$ from [Reference Mirković and VilonenMV07, § 2] which sends
$\check {\delta }$ from [Reference Mirković and VilonenMV07, § 2] which sends ![]() $u$ to
$u$ to ![]() $\alpha u$. Equation (2.4) in [Reference Mirković and VilonenMV07] says that
$\alpha u$. Equation (2.4) in [Reference Mirković and VilonenMV07] says that ![]() $\mathbf {G}_m$ action of
$\mathbf {G}_m$ action of ![]() $\check {\delta }$ contracts
$\check {\delta }$ contracts ![]() $\operatorname {Gr}^{\circ,\mu '}_{G}$ onto
$\operatorname {Gr}^{\circ,\mu '}_{G}$ onto ![]() $X_{\mu '}$. It is easy to see that
$X_{\mu '}$. It is easy to see that ![]() $\operatorname {LG}^{\nabla }$ is stable under
$\operatorname {LG}^{\nabla }$ is stable under ![]() $\check {\delta }$. Thus, any component of
$\check {\delta }$. Thus, any component of ![]() $\operatorname {Gr}_{G}^{\circ,\mu ', \nabla }$ must necessarily intersect
$\operatorname {Gr}_{G}^{\circ,\mu ', \nabla }$ must necessarily intersect ![]() $X_{\mu '}$.
$X_{\mu '}$.
Proof of Theorem 5.2.1 Given that ![]() $\mu$ satisfies the hypotheses of Theorem 5.2.1, so does any
$\mu$ satisfies the hypotheses of Theorem 5.2.1, so does any ![]() $\mu ' \leqslant \mu$. Since
$\mu ' \leqslant \mu$. Since ![]() $\operatorname {Gr}_{G}^{\leqslant \mu }$ is topologically the union of
$\operatorname {Gr}_{G}^{\leqslant \mu }$ is topologically the union of ![]() $\operatorname {Gr}^{\circ,\mu '}_{G}$ for
$\operatorname {Gr}^{\circ,\mu '}_{G}$ for ![]() $\mu ' \leqslant \mu$, by Proposition 5.2.5
$\mu ' \leqslant \mu$, by Proposition 5.2.5
To prove Theorem 5.2.1, then, we just need to show that ![]() $\operatorname {Gr}^{\leqslant \mu, \nabla }_{G}$ is reduced.
$\operatorname {Gr}^{\leqslant \mu, \nabla }_{G}$ is reduced.
By (5.2.4), ![]() $G$ acts transitively on each connected component of
$G$ acts transitively on each connected component of ![]() $\operatorname {Gr}^{\leqslant \mu, \nabla }_{G}$. To show that
$\operatorname {Gr}^{\leqslant \mu, \nabla }_{G}$. To show that ![]() $\operatorname {Gr}^{\leqslant \mu, \nabla }_{G}$ is reduced, it therefore suffices to show that the dimension of the tangent space at
$\operatorname {Gr}^{\leqslant \mu, \nabla }_{G}$ is reduced, it therefore suffices to show that the dimension of the tangent space at ![]() $[u^{\mu '}]$ is equal to
$[u^{\mu '}]$ is equal to ![]() $\dim P_{\mu '} \backslash G$ which follows from Proposition 5.2.3.
$\dim P_{\mu '} \backslash G$ which follows from Proposition 5.2.3.
6. Proof of the main theorem
Let ![]() $\Lambda$,
$\Lambda$, ![]() $\mathbf {F}$,
$\mathbf {F}$, ![]() $L$, and
$L$, and ![]() $G$ be as before, and continue to assume that
$G$ be as before, and continue to assume that ![]() $p \nmid \# \pi _1(G^{\operatorname {der}})$. Throughout this section, we fix a
$p \nmid \# \pi _1(G^{\operatorname {der}})$. Throughout this section, we fix a ![]() $G$-Kisin module
$G$-Kisin module ![]() $\overline {\mathfrak {P}}$ over
$\overline {\mathfrak {P}}$ over ![]() $\mathbf {F}$ and a continuous Galois representation
$\mathbf {F}$ and a continuous Galois representation ![]() ${\overline {\rho }}: \Gamma _K \to G(\mathbf {F})$ together with an isomorphism
${\overline {\rho }}: \Gamma _K \to G(\mathbf {F})$ together with an isomorphism ![]() $\widetilde {T}_{G,\mathbf {F}}(\overline {\mathfrak {P}}) \simeq {\overline {\rho }}|_{\Gamma _\infty }$ as we did in § 3.3 to define our deformation problems.
$\widetilde {T}_{G,\mathbf {F}}(\overline {\mathfrak {P}}) \simeq {\overline {\rho }}|_{\Gamma _\infty }$ as we did in § 3.3 to define our deformation problems.
6.1 Kisin varieties
We begin by studying the Kisin variety and identifying some conditions that guarantee it is trivial.
Definition 6.1.1 Fix ![]() $\mathcal {P} \in \operatorname {GMod}^{\varphi }_{\mathcal {O}_{\mathcal {E}}, \mathbf {F}}$ and a dominant cocharacter
$\mathcal {P} \in \operatorname {GMod}^{\varphi }_{\mathcal {O}_{\mathcal {E}}, \mathbf {F}}$ and a dominant cocharacter ![]() $\mu$ for
$\mu$ for ![]() $G'$. The Kisin variety
$G'$. The Kisin variety ![]() $Y_{\mathcal {P}}^{\leqslant \mu }$ is the projective scheme over
$Y_{\mathcal {P}}^{\leqslant \mu }$ is the projective scheme over ![]() $\mathbf {F}$ which represents the functor sending an
$\mathbf {F}$ which represents the functor sending an ![]() $\mathbf {F}$-algebra
$\mathbf {F}$-algebra ![]() $A$ to the set of
$A$ to the set of ![]() $G$-Kisin lattices of type
$G$-Kisin lattices of type ![]() $\leqslant \mu$ in
$\leqslant \mu$ in ![]() $\mathcal {P}_A$.
$\mathcal {P}_A$.
Let ![]() $\mathcal {P} = M_{G,\mathbf {F}}({\overline {\rho }}|_{\Gamma _\infty })$ and
$\mathcal {P} = M_{G,\mathbf {F}}({\overline {\rho }}|_{\Gamma _\infty })$ and ![]() $\mathfrak {m}$ be the maximal ideal of
$\mathfrak {m}$ be the maximal ideal of ![]() $R^{\mu,\square }_{\overline {\rho }}$. The Kisin variety is an ‘upper bound’ on the fiber of
$R^{\mu,\square }_{\overline {\rho }}$. The Kisin variety is an ‘upper bound’ on the fiber of ![]() $X^{\mu }_{{\overline {\rho }}}$ over
$X^{\mu }_{{\overline {\rho }}}$ over ![]() ${\overline {\rho }}$. More precisely, Proposition 3.3.8(ii) gives an inclusion
${\overline {\rho }}$. More precisely, Proposition 3.3.8(ii) gives an inclusion
Lemma 6.1.2 Suppose ![]() $\mu$ is Fontaine–Laffaille and
$\mu$ is Fontaine–Laffaille and ![]() $A$ is a local Artinian
$A$ is a local Artinian ![]() $\mathbf {F}$-algebra with residue field
$\mathbf {F}$-algebra with residue field ![]() $\mathbf {F}'$. Fix
$\mathbf {F}'$. Fix ![]() $x \in X^{\mu }_{{\overline {\rho }}}(\mathbf {F}')$ and a lift
$x \in X^{\mu }_{{\overline {\rho }}}(\mathbf {F}')$ and a lift ![]() $\widetilde {x} \in \operatorname {Spf}(\widehat {\mathcal {O}}_x^{\mu })(A)$ where
$\widetilde {x} \in \operatorname {Spf}(\widehat {\mathcal {O}}_x^{\mu })(A)$ where ![]() $\widehat {\mathcal {O}}_x^{\mu }$ is the completion of
$\widehat {\mathcal {O}}_x^{\mu }$ is the completion of ![]() $X^{\mu }_{{\overline {\rho }}}$ at
$X^{\mu }_{{\overline {\rho }}}$ at ![]() $x$. The
$x$. The ![]() $G$-Kisin module
$G$-Kisin module ![]() $\mathfrak {P}$ corresponding to
$\mathfrak {P}$ corresponding to ![]() $\widetilde {x}$ using Proposition 3.3.8(i) satisfies the mod-
$\widetilde {x}$ using Proposition 3.3.8(i) satisfies the mod-![]() $p$ monodromy condition.
$p$ monodromy condition.
Proof. Note that ![]() $\widehat {\mathcal {O}}_x^{\mu }$ is
$\widehat {\mathcal {O}}_x^{\mu }$ is ![]() $\Lambda$-flat and reduced by Proposition 3.3.8(iii) and Fact 2.4.2. Since
$\Lambda$-flat and reduced by Proposition 3.3.8(iii) and Fact 2.4.2. Since ![]() $\Theta [1/p]$ is an isomorphism, the
$\Theta [1/p]$ is an isomorphism, the ![]() $\overline {L}$-points of
$\overline {L}$-points of ![]() $\widehat {\mathcal {O}}_x^{\mu }$ correspond to crystalline representations with
$\widehat {\mathcal {O}}_x^{\mu }$ correspond to crystalline representations with ![]() $p$-adic Hodge type
$p$-adic Hodge type ![]() $\mu$. Using Corollary 4.1.11 we conclude that
$\mu$. Using Corollary 4.1.11 we conclude that ![]() $I_{N_{\infty }} = 0$. The lemma then follows from Corollary 4.2.8.
$I_{N_{\infty }} = 0$. The lemma then follows from Corollary 4.2.8.
We set ![]() $\mathbf {K} := G(\mathbf {F}[\![u ] \!])$, and begin by recalling several useful facts related to the Cartan decomposition. We fix a split maximal torus
$\mathbf {K} := G(\mathbf {F}[\![u ] \!])$, and begin by recalling several useful facts related to the Cartan decomposition. We fix a split maximal torus ![]() $T$ contained in a Borel
$T$ contained in a Borel ![]() $B$ and adopt our standard notation for root systems (see § 1.3.1). Let
$B$ and adopt our standard notation for root systems (see § 1.3.1). Let ![]() $T^{\operatorname {der}}$ be the corresponding maximal torus of
$T^{\operatorname {der}}$ be the corresponding maximal torus of ![]() $G^{\operatorname {der}}$.
$G^{\operatorname {der}}$.
Fact 6.1.3 We have that:
(i) (Cartan Decomposition)
 $G(\mathbf {F}(\!(u ) \!)) = \coprod _{\mu \in X_*(T)_+} \mathbf {K} u^\mu \mathbf {K}$;
$G(\mathbf {F}(\!(u ) \!)) = \coprod _{\mu \in X_*(T)_+} \mathbf {K} u^\mu \mathbf {K}$;(ii) for
 $\mu, \lambda, \omega \in X_*(T)_+$, if
$\mu, \lambda, \omega \in X_*(T)_+$, if  $\mathbf {K} u^\lambda \mathbf {K} u ^ {\omega } \mathbf {K} \cap \mathbf {K} u^\mu \mathbf {K} \neq \emptyset$, then
$\mathbf {K} u^\lambda \mathbf {K} u ^ {\omega } \mathbf {K} \cap \mathbf {K} u^\mu \mathbf {K} \neq \emptyset$, then  $\mu \leqslant \lambda + \omega$.
$\mu \leqslant \lambda + \omega$.
The first is the standard Cartan decomposition; see, for example, [Reference TitsTit79, 3.3.3]. The second is a special case of [Reference Bruhat and TitsBT67, Proposition 4.4.4(iii)]; this is somewhat complicated to apply but we do not know a more direct reference. The footnote in [Reference Henniart and VignérasHV15, § 6.9] explains how to translate our set-up into the language of [Reference Bruhat and TitsBT67, Proposition 4.4.4]. The ![]() $K$ in [Reference Bruhat and TitsBT67] is actually a larger group containing
$K$ in [Reference Bruhat and TitsBT67] is actually a larger group containing ![]() $\mathbf {K}$, which is harmless.
$\mathbf {K}$, which is harmless.
Lemma 6.1.4 For dominant coweights ![]() $\mu, \lambda, \omega, \nu$, if
$\mu, \lambda, \omega, \nu$, if ![]() $\mathbf {K} u ^\lambda \mathbf {K} u^{\omega } \mathbf {K} u^{\nu } \mathbf {K} \cap \mathbf {K} u^\mu \mathbf {K} \neq \emptyset$ then
$\mathbf {K} u ^\lambda \mathbf {K} u^{\omega } \mathbf {K} u^{\nu } \mathbf {K} \cap \mathbf {K} u^\mu \mathbf {K} \neq \emptyset$ then ![]() $\mu \leqslant \lambda + \omega + \nu$.
$\mu \leqslant \lambda + \omega + \nu$.
Proof. Apply Fact 6.1.3(ii) twice.
Given a coweight ![]() $\lambda$, define
$\lambda$, define ![]() $\lambda ^{\operatorname {dom}}$ to be the unique dominant coweight in the same Weyl orbit.
$\lambda ^{\operatorname {dom}}$ to be the unique dominant coweight in the same Weyl orbit.
Lemma 6.1.5 Let ![]() $\mu = (\mu _\sigma )_{\sigma \in \mathcal {J}}$ be a type for
$\mu = (\mu _\sigma )_{\sigma \in \mathcal {J}}$ be a type for ![]() $G$. If
$G$. If ![]() $g \in \prod _{ \sigma \in \mathcal {J}} \mathbf {K} u^{\mu _\sigma } \mathbf {K}$, then
$g \in \prod _{ \sigma \in \mathcal {J}} \mathbf {K} u^{\mu _\sigma } \mathbf {K}$, then
(i)
 $g^{-1}_\sigma \in \mathbf {K} u^{(-\mu _\sigma )^{\operatorname {dom}}} \mathbf {K}$.
$g^{-1}_\sigma \in \mathbf {K} u^{(-\mu _\sigma )^{\operatorname {dom}}} \mathbf {K}$.(ii)
 $\varphi (g)_{\sigma \varphi } \in \mathbf {K} u^{p \mu _\sigma } \mathbf {K}$.
$\varphi (g)_{\sigma \varphi } \in \mathbf {K} u^{p \mu _\sigma } \mathbf {K}$.
Proof. This is clear.
Let ![]() $\Phi _{G}^{\operatorname {high}}$ denote the set of highest roots of the irreducible root systems which appear in the irreducible decomposition of the root system of
$\Phi _{G}^{\operatorname {high}}$ denote the set of highest roots of the irreducible root systems which appear in the irreducible decomposition of the root system of ![]() $G$. Recall that
$G$. Recall that ![]() $h_\mu = \max _{\alpha \in \Phi _{G'}} \langle \mu,\alpha \rangle$.
$h_\mu = \max _{\alpha \in \Phi _{G'}} \langle \mu,\alpha \rangle$.
Proposition 6.1.6 Let ![]() $\mathcal {P} = (P,\phi ) \in \operatorname {GMod}^{\varphi }_{\mathcal {O}_{\mathcal {E}},\mathbf {F}}$ and
$\mathcal {P} = (P,\phi ) \in \operatorname {GMod}^{\varphi }_{\mathcal {O}_{\mathcal {E}},\mathbf {F}}$ and ![]() $\mu$ be a dominant type of
$\mu$ be a dominant type of ![]() $G$ such that for every non-zero dominant coweight
$G$ such that for every non-zero dominant coweight ![]() $\lambda$ of
$\lambda$ of ![]() $G^{\operatorname {der}}$ there exists
$G^{\operatorname {der}}$ there exists ![]() $\alpha _h \in \Phi _G^{\operatorname {high}}$ such that
$\alpha _h \in \Phi _G^{\operatorname {high}}$ such that
Then for any finite extension ![]() $\mathbf {F}' / \mathbf {F}$ there is at most one
$\mathbf {F}' / \mathbf {F}$ there is at most one ![]() $G$-Kisin lattice of type
$G$-Kisin lattice of type ![]() $\leqslant \mu$ in
$\leqslant \mu$ in ![]() $\mathcal {P}_{\mathbf {F}'}$ (up to isomorphism).
$\mathcal {P}_{\mathbf {F}'}$ (up to isomorphism).
Proof. Suppose that ![]() $(\mathfrak {P}',\alpha ')$ and
$(\mathfrak {P}',\alpha ')$ and ![]() $(\mathfrak {P}'',\alpha '')$ are two
$(\mathfrak {P}'',\alpha '')$ are two ![]() $G$-Kisin lattices in
$G$-Kisin lattices in ![]() $\mathcal {P}_{\mathbf {F}'} = (P_{\mathbf {F}'}, \phi _{P_{\mathbf {F}'}})$. After trivializing
$\mathcal {P}_{\mathbf {F}'} = (P_{\mathbf {F}'}, \phi _{P_{\mathbf {F}'}})$. After trivializing ![]() $P_{\mathbf {F}'}$ and identifying
$P_{\mathbf {F}'}$ and identifying ![]() $\epsilon _G(\mathfrak {P}')$ and
$\epsilon _G(\mathfrak {P}')$ and ![]() $\epsilon _G(\mathfrak {P}'')$ with
$\epsilon _G(\mathfrak {P}'')$ with ![]() $P_{\mathbf {F}'}$, we obtain
$P_{\mathbf {F}'}$, we obtain ![]() $A, \Phi$, and
$A, \Phi$, and ![]() $\Phi '$ in
$\Phi '$ in ![]() $G'(\mathbf {F}'(\!(u ) \!))$ such that
$G'(\mathbf {F}'(\!(u ) \!))$ such that
Write ![]() $A = (A_\sigma )_{\sigma \in \mathcal {J}}$,
$A = (A_\sigma )_{\sigma \in \mathcal {J}}$, ![]() $\Phi ' = (\Phi '_\sigma )_{\sigma \in \mathcal {J}},$ and
$\Phi ' = (\Phi '_\sigma )_{\sigma \in \mathcal {J}},$ and ![]() $\Phi '' = (\Phi ''_\sigma )_{\sigma \in \mathcal {J}}$. As the
$\Phi '' = (\Phi ''_\sigma )_{\sigma \in \mathcal {J}}$. As the ![]() $G$-Kisin lattices are of type
$G$-Kisin lattices are of type ![]() $\leqslant \mu$, we know that there are dominant cocharacters
$\leqslant \mu$, we know that there are dominant cocharacters ![]() $\mu ', \mu '' \leqslant \mu$ such that for each
$\mu ', \mu '' \leqslant \mu$ such that for each ![]() $\sigma \in \mathcal {J}$ we have
$\sigma \in \mathcal {J}$ we have ![]() $\Phi '_\sigma \in \mathbf {K} u ^{\mu '_\sigma } \mathbf {K}$ and
$\Phi '_\sigma \in \mathbf {K} u ^{\mu '_\sigma } \mathbf {K}$ and ![]() $\Phi ''_\sigma \in \mathbf {K} u ^{\mu ''_\sigma } \mathbf {K}$. There is a unique dominant coweight
$\Phi ''_\sigma \in \mathbf {K} u ^{\mu ''_\sigma } \mathbf {K}$. There is a unique dominant coweight ![]() $\lambda$ of
$\lambda$ of ![]() $G'$ such that
$G'$ such that ![]() $A_\sigma \in \mathbf {K} u^{\lambda _\sigma } \mathbf {K}$ for each
$A_\sigma \in \mathbf {K} u^{\lambda _\sigma } \mathbf {K}$ for each ![]() $\sigma \in \mathcal {J}$. It suffices to show that
$\sigma \in \mathcal {J}$. It suffices to show that ![]() $\lambda =0$ so that
$\lambda =0$ so that ![]() $A \in G'(\mathbf {F}'[\![u ] \!])$.
$A \in G'(\mathbf {F}'[\![u ] \!])$.
Working with components as in Example 3.1.6, we note that (6.1.2) is equivalent to
We know that ![]() $(\Phi ''_{\sigma })^{-1} \in \mathbf {K} u^{(-\mu _{\sigma } '')^{\operatorname {dom}}} \mathbf {K}$ and that
$(\Phi ''_{\sigma })^{-1} \in \mathbf {K} u^{(-\mu _{\sigma } '')^{\operatorname {dom}}} \mathbf {K}$ and that ![]() $\varphi (A)_{\sigma } \in \mathbf {K} u^{p \lambda _{\sigma \varphi ^{-1}}} \mathbf {K}$ by Lemma 6.1.5. Applying Lemma 6.1.4 to (6.1.3) gives that
$\varphi (A)_{\sigma } \in \mathbf {K} u^{p \lambda _{\sigma \varphi ^{-1}}} \mathbf {K}$ by Lemma 6.1.5. Applying Lemma 6.1.4 to (6.1.3) gives that
In other words, ![]() $\mu '_\sigma + (-\mu ''_\sigma )^{\operatorname {dom}} - p \lambda _{\sigma \varphi ^{-1}} + \lambda _{\sigma }$ is a non-negative linear combination of simple coroots. Since any
$\mu '_\sigma + (-\mu ''_\sigma )^{\operatorname {dom}} - p \lambda _{\sigma \varphi ^{-1}} + \lambda _{\sigma }$ is a non-negative linear combination of simple coroots. Since any ![]() $\alpha _h \in \Phi _G^{\operatorname {high}}$ pairs non-negatively with positive coroots, this implies
$\alpha _h \in \Phi _G^{\operatorname {high}}$ pairs non-negatively with positive coroots, this implies
Now as ![]() $\mu ', \mu '' \leqslant \mu$, the difference
$\mu ', \mu '' \leqslant \mu$, the difference ![]() $\mu '_\sigma - \mu ''_\sigma$ is a combination of simple coroots for each
$\mu '_\sigma - \mu ''_\sigma$ is a combination of simple coroots for each ![]() $\sigma \in \mathcal {J}$. Then
$\sigma \in \mathcal {J}$. Then ![]() $\mu '_\sigma - \mu ''_\sigma$ and, hence,
$\mu '_\sigma - \mu ''_\sigma$ and, hence, ![]() $\mu '_\sigma + (- \mu ''_{\sigma })^{\operatorname {dom}}$ is in
$\mu '_\sigma + (- \mu ''_{\sigma })^{\operatorname {dom}}$ is in ![]() $X_*(T^{\operatorname {der}})$. Likewise, we see
$X_*(T^{\operatorname {der}})$. Likewise, we see ![]() $p \lambda _{\sigma \varphi ^{_1}} - \lambda _\sigma \in X_*(T^{\operatorname {der}})$ for each
$p \lambda _{\sigma \varphi ^{_1}} - \lambda _\sigma \in X_*(T^{\operatorname {der}})$ for each ![]() $\sigma \in \mathcal {J}$ and, hence, that
$\sigma \in \mathcal {J}$ and, hence, that ![]() $(p^{\# \mathcal {J}} -1) \lambda _{\sigma } \in X_*(T^{\operatorname {der}})$. As the quotient of
$(p^{\# \mathcal {J}} -1) \lambda _{\sigma } \in X_*(T^{\operatorname {der}})$. As the quotient of ![]() $X_*(T^{\operatorname {der}}) \to X_*(T^{\operatorname {der}})$ is torsion-free, we conclude that
$X_*(T^{\operatorname {der}}) \to X_*(T^{\operatorname {der}})$ is torsion-free, we conclude that ![]() $\lambda _{\sigma }$ is a cocharacter valued in
$\lambda _{\sigma }$ is a cocharacter valued in ![]() $G^{\operatorname {der}}$.
$G^{\operatorname {der}}$.
Fix a ![]() $\sigma \in \mathcal {J}$ and
$\sigma \in \mathcal {J}$ and ![]() $\alpha _h \in \Phi _G^{\operatorname {high}}$ that maximize
$\alpha _h \in \Phi _G^{\operatorname {high}}$ that maximize ![]() $\langle \lambda _{\sigma \varphi ^{-1}},\alpha _h \rangle$: if
$\langle \lambda _{\sigma \varphi ^{-1}},\alpha _h \rangle$: if ![]() $\lambda \neq 0$ then
$\lambda \neq 0$ then ![]() $(p-1)\langle \lambda _{\sigma \varphi ^{-1}},\alpha _h \rangle >2 h_\mu$ by hypothesis. There is an element
$(p-1)\langle \lambda _{\sigma \varphi ^{-1}},\alpha _h \rangle >2 h_\mu$ by hypothesis. There is an element ![]() $w$ of the Weyl group such that
$w$ of the Weyl group such that ![]() $w (-\mu ''_\sigma )^{\operatorname {dom}} = -\mu ''_\sigma$ and, hence,
$w (-\mu ''_\sigma )^{\operatorname {dom}} = -\mu ''_\sigma$ and, hence,
Likewise as ![]() $\mu ' \leqslant \mu$ we see that
$\mu ' \leqslant \mu$ we see that ![]() $\langle \mu '_\sigma, \alpha _h \rangle \leqslant h_\mu$. We know
$\langle \mu '_\sigma, \alpha _h \rangle \leqslant h_\mu$. We know ![]() $\langle \lambda _{\sigma } ,\alpha _h \rangle \leqslant \langle \lambda _{\sigma \varphi ^{-1}}, \alpha _h \rangle$ by choice of
$\langle \lambda _{\sigma } ,\alpha _h \rangle \leqslant \langle \lambda _{\sigma \varphi ^{-1}}, \alpha _h \rangle$ by choice of ![]() $\sigma$, so we see that
$\sigma$, so we see that
This contradiction shows that ![]() $\lambda = 0$.
$\lambda = 0$.
We next show that the hypothesis on ![]() $\mu$ in Proposition 6.1.6 is satisfied when
$\mu$ in Proposition 6.1.6 is satisfied when ![]() $\mu$ is sufficiently small.
$\mu$ is sufficiently small.
Lemma 6.1.7 Let ![]() $\mu$ be a dominant type for
$\mu$ be a dominant type for ![]() $G$. For every non-zero dominant cocharacter
$G$. For every non-zero dominant cocharacter ![]() $\lambda$ of
$\lambda$ of ![]() $G^{\operatorname {der}}$, there exists
$G^{\operatorname {der}}$, there exists ![]() $\alpha _h \in \Phi _G^{\operatorname {high}}$ such that
$\alpha _h \in \Phi _G^{\operatorname {high}}$ such that
provided that:
(i)
 $\mu$ is strongly Fontaine–Laffaille (i.e.
$\mu$ is strongly Fontaine–Laffaille (i.e.  $\langle \mu, \alpha \rangle < ({p-1})/{2}$ for every
$\langle \mu, \alpha \rangle < ({p-1})/{2}$ for every  $\alpha \in \Phi _{G'}$); or
$\alpha \in \Phi _{G'}$); or(ii)
 $\mu$ is Fontaine–Laffaille (i.e.
$\mu$ is Fontaine–Laffaille (i.e.  $\langle \mu, \alpha \rangle < p-1$ for every
$\langle \mu, \alpha \rangle < p-1$ for every  $\alpha \in \Phi _{G'}$) and there are no non-zero coweights
$\alpha \in \Phi _{G'}$) and there are no non-zero coweights  $\lambda$ of
$\lambda$ of  $G$ such that
$G$ such that  $\langle \lambda, \alpha _h \rangle \leqslant 1$ for all
$\langle \lambda, \alpha _h \rangle \leqslant 1$ for all  $\alpha _h \in \Phi _G^{\operatorname {high}}$; or
$\alpha _h \in \Phi _G^{\operatorname {high}}$; or(iii)
 $\mu$ is Fontaine–Laffaille and
$\mu$ is Fontaine–Laffaille and  $G^{\operatorname {der}}$ is simply connected.
$G^{\operatorname {der}}$ is simply connected.
Proof. The first and second are immediate, as ![]() $\langle \lambda,\alpha _h\rangle$ must be a positive integer for any non-zero dominant coweight
$\langle \lambda,\alpha _h\rangle$ must be a positive integer for any non-zero dominant coweight ![]() $\lambda$.
$\lambda$.
When the root system of ![]() $G$ is irreducible and
$G$ is irreducible and ![]() $G^{\operatorname {der}}$ is simply connected, it turns out there are no coweights
$G^{\operatorname {der}}$ is simply connected, it turns out there are no coweights ![]() $\lambda$ with
$\lambda$ with ![]() $\langle \lambda, \alpha _h \rangle =1$ so the third follows from the second. In particular, the condition
$\langle \lambda, \alpha _h \rangle =1$ so the third follows from the second. In particular, the condition ![]() $\langle \lambda, \alpha _h \rangle =1$ is one of several equivalent definitions for
$\langle \lambda, \alpha _h \rangle =1$ is one of several equivalent definitions for ![]() $\lambda$ being a minuscule weight of the dual root system; see [Reference BourbakiBou05, Ch. VIII, § 7.3] for the properties of minuscule weights. Let
$\lambda$ being a minuscule weight of the dual root system; see [Reference BourbakiBou05, Ch. VIII, § 7.3] for the properties of minuscule weights. Let ![]() $\alpha _1, \ldots, \alpha _r$ be the positive simple roots, and write
$\alpha _1, \ldots, \alpha _r$ be the positive simple roots, and write
with the ![]() $n_i$ positive integers. Then
$n_i$ positive integers. Then ![]() $\lambda$ being minuscule is equivalent to the condition that
$\lambda$ being minuscule is equivalent to the condition that ![]() $\lambda = \varpi ^\vee _i$ for some fundamental weight
$\lambda = \varpi ^\vee _i$ for some fundamental weight ![]() $\varpi ^\vee _i$ with
$\varpi ^\vee _i$ with ![]() $n_i=1$ (see [Reference BourbakiBou05, VIII § 7.3, Proposition 8]). Furthermore, the minuscule
$n_i=1$ (see [Reference BourbakiBou05, VIII § 7.3, Proposition 8]). Furthermore, the minuscule ![]() $\varpi _i^\vee$ form a system of representatives for
$\varpi _i^\vee$ form a system of representatives for ![]() $P(\Phi _G^\vee )/ Q(\Phi _G^\vee )$. However,
$P(\Phi _G^\vee )/ Q(\Phi _G^\vee )$. However, ![]() $G$ is simply connected, so
$G$ is simply connected, so ![]() $X^*(T) = P(\Phi _G)$ and
$X^*(T) = P(\Phi _G)$ and ![]() $X_*(T) = Q(\Phi _G^\vee )$. Thus, none of the minuscule coweights lie in the cocharacter group, so there are no dominant minuscule cocharacters. Therefore, there are no coweights
$X_*(T) = Q(\Phi _G^\vee )$. Thus, none of the minuscule coweights lie in the cocharacter group, so there are no dominant minuscule cocharacters. Therefore, there are no coweights ![]() $\lambda$ with
$\lambda$ with ![]() $\langle \lambda, \alpha _h \rangle =1$.
$\langle \lambda, \alpha _h \rangle =1$.
If ![]() $G^{\operatorname {der}}$ is simply connected but the root system is not irreducible, decompose the root system into irreducibles and write
$G^{\operatorname {der}}$ is simply connected but the root system is not irreducible, decompose the root system into irreducibles and write ![]() $G^{\operatorname {der}}$ as a product of simply connected groups with irreducible root systems. The claim follows as the decomposition of the root system is orthogonal.
$G^{\operatorname {der}}$ as a product of simply connected groups with irreducible root systems. The claim follows as the decomposition of the root system is orthogonal.
Corollary 6.1.8 Let ![]() $\mathcal {P} \in \operatorname {GMod}^{\varphi }_{\mathcal {O}_{\mathcal {E}},\mathbf {F}}$ and
$\mathcal {P} \in \operatorname {GMod}^{\varphi }_{\mathcal {O}_{\mathcal {E}},\mathbf {F}}$ and ![]() $\mu$ be a dominant cocharacter of
$\mu$ be a dominant cocharacter of ![]() $G'$ such that either:
$G'$ such that either:
(i)
 $\mu$ is strongly Fontaine–Laffaille; or
$\mu$ is strongly Fontaine–Laffaille; or(ii)
 $\mu$ is Fontaine–Laffaille and
$\mu$ is Fontaine–Laffaille and  $G^{\operatorname {der}}$ is simply connected.
$G^{\operatorname {der}}$ is simply connected.
Then for any finite extension ![]() $\mathbf {F}'$ of
$\mathbf {F}'$ of ![]() $\mathbf {F}$, we have
$\mathbf {F}$, we have ![]() $Y_{\mathcal {P}}^{\leqslant \mu } (\mathbf {F}')$ is either empty or a single element.
$Y_{\mathcal {P}}^{\leqslant \mu } (\mathbf {F}')$ is either empty or a single element.
Next we establish a result about tangent spaces.
Proposition 6.1.9 Fix a finite extension ![]() $\mathbf {F}' / \mathbf {F}$, a dominant cocharacter
$\mathbf {F}' / \mathbf {F}$, a dominant cocharacter ![]() $\mu$ of
$\mu$ of ![]() $G'$ in the Fontaine–Laffaille range, and
$G'$ in the Fontaine–Laffaille range, and ![]() $\overline {\mathfrak {P}} \in Y^{\leqslant \mu }(\mathbf {F}')$. Consider lifts
$\overline {\mathfrak {P}} \in Y^{\leqslant \mu }(\mathbf {F}')$. Consider lifts ![]() $\mathfrak {P}_1, \mathfrak {P}_2 \in Y^{\leqslant \mu }(\mathbf {F}'[\epsilon ]/(\epsilon ^2))$ of
$\mathfrak {P}_1, \mathfrak {P}_2 \in Y^{\leqslant \mu }(\mathbf {F}'[\epsilon ]/(\epsilon ^2))$ of ![]() $\overline {\mathfrak {P}}$ that satisfy the mod-
$\overline {\mathfrak {P}}$ that satisfy the mod-![]() $p$ monodromy condition. If
$p$ monodromy condition. If ![]() $\epsilon _G(\mathfrak {P}_1) \simeq \epsilon _G(\mathfrak {P}_2)$ compatibly with the identification of the reduction with
$\epsilon _G(\mathfrak {P}_1) \simeq \epsilon _G(\mathfrak {P}_2)$ compatibly with the identification of the reduction with ![]() $\overline {\mathfrak {P}}$, then
$\overline {\mathfrak {P}}$, then ![]() $\mathfrak {P}_1$ and
$\mathfrak {P}_1$ and ![]() $\mathfrak {P}_2$ are isomorphic as deformations of
$\mathfrak {P}_2$ are isomorphic as deformations of ![]() $\,\overline {\mathfrak {P}}$.
$\,\overline {\mathfrak {P}}$.
We continue our standard notation of ![]() $\operatorname {LG}'$,
$\operatorname {LG}'$, ![]() $\textrm {L}^+G'$,
$\textrm {L}^+G'$, ![]() $\operatorname {Gr}_{G'}$,
$\operatorname {Gr}_{G'}$, ![]() $\operatorname {Gr}^{\leqslant \mu }_{G'}$ and
$\operatorname {Gr}^{\leqslant \mu }_{G'}$ and ![]() $\operatorname {Gr}^{\circ, \leqslant \mu }_{G'_{\mathbf {F}}}$ for loop groups and affine Grassmanians as summarized in § 1.3.3, and use the description of the tangent space to
$\operatorname {Gr}^{\circ, \leqslant \mu }_{G'_{\mathbf {F}}}$ for loop groups and affine Grassmanians as summarized in § 1.3.3, and use the description of the tangent space to ![]() $\operatorname {Gr}^{\circ, \leqslant \mu }_{G'_{\mathbf {F}}}$ provided by Lemma 2.3.3. For
$\operatorname {Gr}^{\circ, \leqslant \mu }_{G'_{\mathbf {F}}}$ provided by Lemma 2.3.3. For ![]() $C \in \operatorname {LG}'$, let
$C \in \operatorname {LG}'$, let ![]() $m_C$ denote the right multiplication by
$m_C$ denote the right multiplication by ![]() $C$ map on
$C$ map on ![]() $\operatorname {LG}'$ or
$\operatorname {LG}'$ or ![]() $\operatorname {Gr}_{G'}$.
$\operatorname {Gr}_{G'}$.
Remark 6.1.10 An ![]() $\mathbf {F}'[\epsilon ]/(\epsilon ^2)$-valued point of
$\mathbf {F}'[\epsilon ]/(\epsilon ^2)$-valued point of ![]() $\operatorname {LG}'$ corresponds to an
$\operatorname {LG}'$ corresponds to an ![]() $\mathbf {F}'$-valued point of
$\mathbf {F}'$-valued point of ![]() $\operatorname {LG}'$ plus a tangent vector to
$\operatorname {LG}'$ plus a tangent vector to ![]() $\operatorname {LG}'$ at that point; let
$\operatorname {LG}'$ at that point; let ![]() $\iota$ denote the identification of tangent vectors with
$\iota$ denote the identification of tangent vectors with ![]() $\mathbf {F}[\epsilon ]/(\epsilon ^2)$-points. At the identity, multiplication of
$\mathbf {F}[\epsilon ]/(\epsilon ^2)$-points. At the identity, multiplication of ![]() $\mathbf {F}[\epsilon ]/(\epsilon ^2)$-points corresponds to addition in the Lie algebra. For use in the proof of Proposition 6.1.9, we record how multiplication on
$\mathbf {F}[\epsilon ]/(\epsilon ^2)$-points corresponds to addition in the Lie algebra. For use in the proof of Proposition 6.1.9, we record how multiplication on ![]() $\mathbf {F}'[\epsilon ]/(\epsilon ^2)$-points interacts with identifying the tangent spaces with the Lie algebra via translation.
$\mathbf {F}'[\epsilon ]/(\epsilon ^2)$-points interacts with identifying the tangent spaces with the Lie algebra via translation.
For ![]() $C \in \operatorname {LG}'(\mathbf {F}')$, the derivative
$C \in \operatorname {LG}'(\mathbf {F}')$, the derivative ![]() $d m_{C}$ induces an isomorphism between the tangent space of
$d m_{C}$ induces an isomorphism between the tangent space of ![]() $\operatorname {LG}'$ at the identity and the tangent space of
$\operatorname {LG}'$ at the identity and the tangent space of ![]() $\operatorname {LG}'$ at
$\operatorname {LG}'$ at ![]() $C$. Given
$C$. Given ![]() $Y_1, Y_2$ in the Lie algebra, set
$Y_1, Y_2$ in the Lie algebra, set ![]() $B_i := \iota (Y_i)$ so, for example,
$B_i := \iota (Y_i)$ so, for example, ![]() $\iota ( dm_C(Y_2)) = B_2 C$. As
$\iota ( dm_C(Y_2)) = B_2 C$. As
we conclude that ![]() $B_1 C B_2 = \iota ( dm_C( Y_1 + \operatorname {Ad}_G(C) (Y_2)))$. In contrast,
$B_1 C B_2 = \iota ( dm_C( Y_1 + \operatorname {Ad}_G(C) (Y_2)))$. In contrast, ![]() $B_2 m_C(B_1) = B_2 B_1 C = m_C(B_2 B_1) = \iota ( dm_C(Y_2 + Y_1))$.
$B_2 m_C(B_1) = B_2 B_1 C = m_C(B_2 B_1) = \iota ( dm_C(Y_2 + Y_1))$.
Proof of Proposition 6.1.9 Trivializing ![]() $\mathfrak {P}_1$ and
$\mathfrak {P}_1$ and ![]() $\mathfrak {P}_2$, we obtain
$\mathfrak {P}_2$, we obtain ![]() $C_1, C_2 \in \operatorname {LG}'(\mathbf {F}'[\epsilon ]/(\epsilon ^2))$ representing
$C_1, C_2 \in \operatorname {LG}'(\mathbf {F}'[\epsilon ]/(\epsilon ^2))$ representing ![]() $\varphi _{\mathfrak {P}_1}$ and
$\varphi _{\mathfrak {P}_1}$ and ![]() $\varphi _{\mathfrak {P}_2}$ and
$\varphi _{\mathfrak {P}_2}$ and ![]() $D \in \operatorname {LG}'(\mathbf {F}'[\epsilon ]/(\epsilon ^2))$ representing the isomorphism
$D \in \operatorname {LG}'(\mathbf {F}'[\epsilon ]/(\epsilon ^2))$ representing the isomorphism ![]() $\epsilon _G(\mathfrak {P}_1) \simeq \epsilon _G(\mathfrak {P}_2)$ such that
$\epsilon _G(\mathfrak {P}_1) \simeq \epsilon _G(\mathfrak {P}_2)$ such that
We know that ![]() $D$ is the identity modulo
$D$ is the identity modulo ![]() $\epsilon$, and that
$\epsilon$, and that ![]() $C_1$ and
$C_1$ and ![]() $C_2$ agree modulo
$C_2$ agree modulo ![]() $\epsilon$. Let
$\epsilon$. Let ![]() $\overline {C} \in \operatorname {LG}'(\mathbf {F}')$ be the common reduction of
$\overline {C} \in \operatorname {LG}'(\mathbf {F}')$ be the common reduction of ![]() $C_1$ and
$C_1$ and ![]() $C_2$; we may write
$C_2$; we may write ![]() $\overline {C} = B_1 u ^{\mu '} B_2$ with
$\overline {C} = B_1 u ^{\mu '} B_2$ with ![]() $B_1, B_2 \in \textrm {L}^+G'(\mathbf {F}')$ and
$B_1, B_2 \in \textrm {L}^+G'(\mathbf {F}')$ and ![]() $\mu ' \leqslant \mu$ as
$\mu ' \leqslant \mu$ as ![]() $\overline {\mathfrak {P}} \in Y^{\leqslant \mu }(\mathbf {F}')$. Using the natural inclusion
$\overline {\mathfrak {P}} \in Y^{\leqslant \mu }(\mathbf {F}')$. Using the natural inclusion ![]() $\mathbf {F}' \hookrightarrow \mathbf {F}'[\epsilon ]/(\epsilon ^2)$, we may also view
$\mathbf {F}' \hookrightarrow \mathbf {F}'[\epsilon ]/(\epsilon ^2)$, we may also view ![]() $\overline {C}$ as an element of
$\overline {C}$ as an element of ![]() $\operatorname {LG}'(\mathbf {F}'[\epsilon ]/(\epsilon ^2))$.
$\operatorname {LG}'(\mathbf {F}'[\epsilon ]/(\epsilon ^2))$.
We wish to show that ![]() $D \in \textrm {L}^+G'(\mathbf {F}')$, which implies that
$D \in \textrm {L}^+G'(\mathbf {F}')$, which implies that ![]() $\mathfrak {P}_1$ and
$\mathfrak {P}_1$ and ![]() $\mathfrak {P}_2$ are equivalent deformations of
$\mathfrak {P}_2$ are equivalent deformations of ![]() $\overline {\mathfrak {P}}$. By appropriate choice of trivializations, without loss of generality we may assume that
$\overline {\mathfrak {P}}$. By appropriate choice of trivializations, without loss of generality we may assume that ![]() $B_1$ is the identity. We rewrite (6.1.6) as
$B_1$ is the identity. We rewrite (6.1.6) as
Note that ![]() $D$ corresponds to a tangent vector at the identity, and
$D$ corresponds to a tangent vector at the identity, and ![]() $C_i B_2^{-1}$ corresponds to a tangent vector at
$C_i B_2^{-1}$ corresponds to a tangent vector at ![]() $u^{\mu '}$. The derivative of the right multiplication map
$u^{\mu '}$. The derivative of the right multiplication map ![]() $m_{u^{\mu '}}$ identifies the tangent space at the identity with the tangent space at
$m_{u^{\mu '}}$ identifies the tangent space at the identity with the tangent space at ![]() $u^{\mu '}$, so there are
$u^{\mu '}$, so there are ![]() $X, Y_1,$ and
$X, Y_1,$ and ![]() $Y_2$ in
$Y_2$ in ![]() $\operatorname {Lie} \operatorname {LG}_{\mathbf {F}'} = \mathfrak {g}_{\mathbf {F}'(\!(u ) \!)}$ such that
$\operatorname {Lie} \operatorname {LG}_{\mathbf {F}'} = \mathfrak {g}_{\mathbf {F}'(\!(u ) \!)}$ such that ![]() $\imath (X)=D$ and
$\imath (X)=D$ and ![]() $\imath (d m_{ u^\mu } (Y_i)) = C_i B_2^{-1}$. Using Remark 6.1.10, they satisfy
$\imath (d m_{ u^\mu } (Y_i)) = C_i B_2^{-1}$. Using Remark 6.1.10, they satisfy
Let ![]() $n$ be the largest integer such that
$n$ be the largest integer such that ![]() $X \in u^n \mathfrak {g}'_{\mathbf {F}'[\![u ] \!]}$. We claim that
$X \in u^n \mathfrak {g}'_{\mathbf {F}'[\![u ] \!]}$. We claim that ![]() $n \geqslant 0$, which shows that
$n \geqslant 0$, which shows that ![]() $X$ lies in
$X$ lies in ![]() $\mathfrak {g}'_{\mathbf {F}'[\![u ] \!]}$. This, in turn, implies that
$\mathfrak {g}'_{\mathbf {F}'[\![u ] \!]}$. This, in turn, implies that ![]() $D \in \textrm {L}^+G'(\mathbf {F}')$ as desired.
$D \in \textrm {L}^+G'(\mathbf {F}')$ as desired.
We begin by considering the left-hand side of (6.1.7). Since ![]() $\mathfrak {P}_1$ and
$\mathfrak {P}_1$ and ![]() $\mathfrak {P}_2$ satisfy the mod-
$\mathfrak {P}_2$ satisfy the mod-![]() $p$ monodromy condition, Corollary 5.2.4 shows that
$p$ monodromy condition, Corollary 5.2.4 shows that
In particular, we see that
On the other hand, as ![]() $B_2 \in \textrm {L}^+G'(\mathbf {F}')$ we know
$B_2 \in \textrm {L}^+G'(\mathbf {F}')$ we know ![]() $\operatorname {Ad}_{G'}(B_2)$ is an invertible linear transformation of
$\operatorname {Ad}_{G'}(B_2)$ is an invertible linear transformation of ![]() $\mathfrak {g}'_{\mathbf {F}'[\![u ] \!]}$ and, hence,
$\mathfrak {g}'_{\mathbf {F}'[\![u ] \!]}$ and, hence, ![]() $\operatorname {Ad}_{G'}(B_2) (\varphi (X))$ lies in
$\operatorname {Ad}_{G'}(B_2) (\varphi (X))$ lies in ![]() $u^{pn} \mathfrak {g}'_{\mathbf {F}'[\![u ] \!]}$ but not
$u^{pn} \mathfrak {g}'_{\mathbf {F}'[\![u ] \!]}$ but not ![]() $u^{pn+1} \mathfrak {g}'_{\mathbf {F}'[\![u ] \!]}$. As
$u^{pn+1} \mathfrak {g}'_{\mathbf {F}'[\![u ] \!]}$. As ![]() $\operatorname {Ad}_{G'}(u^{\mu '})$ acts on the root space
$\operatorname {Ad}_{G'}(u^{\mu '})$ acts on the root space ![]() $\mathfrak {g}'_\alpha$ via multiplication by
$\mathfrak {g}'_\alpha$ via multiplication by ![]() $u^{ \langle \mu ',\alpha \rangle }$ and it acts trivially on
$u^{ \langle \mu ',\alpha \rangle }$ and it acts trivially on ![]() $\mathfrak {t}$, we see that
$\mathfrak {t}$, we see that
We also know there is either a root ![]() $\alpha$ for which the
$\alpha$ for which the ![]() $\mathfrak {g}'_\alpha$-component of
$\mathfrak {g}'_\alpha$-component of ![]() $Z$ does not lie in
$Z$ does not lie in ![]() $u^{pn+1 + \langle \mu ',\alpha \rangle } \mathfrak {g}'_{\alpha, \mathbf {F}'[\![u ] \!]}$ or the
$u^{pn+1 + \langle \mu ',\alpha \rangle } \mathfrak {g}'_{\alpha, \mathbf {F}'[\![u ] \!]}$ or the ![]() $\mathfrak {t}'$-component of
$\mathfrak {t}'$-component of ![]() $Z$ does not lie in
$Z$ does not lie in ![]() $u^{pn+1}\mathfrak {t}'_{\mathbf {F}'[\![u ] \!]}$. In the latter case, if
$u^{pn+1}\mathfrak {t}'_{\mathbf {F}'[\![u ] \!]}$. In the latter case, if ![]() $n<0$, then the
$n<0$, then the ![]() $\mathfrak {t}'$-component of
$\mathfrak {t}'$-component of ![]() $Z = X + Y_1 - Y_2$ does not lie in
$Z = X + Y_1 - Y_2$ does not lie in ![]() $u^n \mathfrak {t}'_{\mathbf {F}'[\![u ] \!]}$, a contradiction. In the former case, this would imply that
$u^n \mathfrak {t}'_{\mathbf {F}'[\![u ] \!]}$, a contradiction. In the former case, this would imply that ![]() $pn + \langle \mu ', \alpha \rangle \geqslant \min ( \langle \mu ',\alpha \rangle ), n)$. If the minimum is
$pn + \langle \mu ', \alpha \rangle \geqslant \min ( \langle \mu ',\alpha \rangle ), n)$. If the minimum is ![]() $\langle \mu ', \alpha \rangle$, then we see that
$\langle \mu ', \alpha \rangle$, then we see that ![]() $pn\geqslant 0$ and, hence,
$pn\geqslant 0$ and, hence, ![]() $n \geqslant 0$. If the minimum is
$n \geqslant 0$. If the minimum is ![]() $n$ we would have
$n$ we would have ![]() $(p-1)n \geqslant - \langle \mu ',\alpha \rangle$. But since
$(p-1)n \geqslant - \langle \mu ',\alpha \rangle$. But since ![]() $\mu$ is Fontaine–Laffaille,
$\mu$ is Fontaine–Laffaille, ![]() $|\langle \mu ', \alpha \rangle | \leqslant |\langle \mu, \alpha \rangle | < p-1$, so we again conclude that
$|\langle \mu ', \alpha \rangle | \leqslant |\langle \mu, \alpha \rangle | < p-1$, so we again conclude that ![]() $n \geqslant 0$.
$n \geqslant 0$.
Corollary 6.1.11 Fix a finite extension ![]() $\mathbf {F}' / \mathbf {F}$,
$\mathbf {F}' / \mathbf {F}$, ![]() $\mu$ in the Fontaine–Laffaille range, and
$\mu$ in the Fontaine–Laffaille range, and ![]() $\overline {\mathfrak {P}} \in Y^{\leqslant \mu }(\mathbf {F}')$. Given lifts
$\overline {\mathfrak {P}} \in Y^{\leqslant \mu }(\mathbf {F}')$. Given lifts ![]() $\mathfrak {P}_1, \mathfrak {P}_2 \in Y^{\leqslant \mu }(\mathbf {F}'[\epsilon ]/(\epsilon ^2))$ of
$\mathfrak {P}_1, \mathfrak {P}_2 \in Y^{\leqslant \mu }(\mathbf {F}'[\epsilon ]/(\epsilon ^2))$ of ![]() $\overline {\mathfrak {P}}$ satisfying the mod-
$\overline {\mathfrak {P}}$ satisfying the mod-![]() $p$ monodromy condition such that
$p$ monodromy condition such that ![]() $\widetilde {T}_{G, \mathbf {F}'[\epsilon ]/(\epsilon ^2)}(\mathfrak {P}_1) \simeq \widetilde {T}_{G,\mathbf {F}'[\epsilon ]/(\epsilon ^2)}( \mathfrak {P}_2)$ (compatible with the identification of the reduction with
$\widetilde {T}_{G, \mathbf {F}'[\epsilon ]/(\epsilon ^2)}(\mathfrak {P}_1) \simeq \widetilde {T}_{G,\mathbf {F}'[\epsilon ]/(\epsilon ^2)}( \mathfrak {P}_2)$ (compatible with the identification of the reduction with ![]() ${\overline {\rho }}|_{\Gamma _\infty } \simeq \widetilde {T}_{G,\mathbf {F}'} (\overline {\mathfrak {P}})$), then
${\overline {\rho }}|_{\Gamma _\infty } \simeq \widetilde {T}_{G,\mathbf {F}'} (\overline {\mathfrak {P}})$), then ![]() $\mathfrak {P}_1$ and
$\mathfrak {P}_1$ and ![]() $\mathfrak {P}_2$ are isomorphic as deformations of
$\mathfrak {P}_2$ are isomorphic as deformations of ![]() $\,\overline {\mathfrak {P}}$.
$\,\overline {\mathfrak {P}}$.
Proof. This is an immediate consequence of Proposition 6.1.9 as ![]() $T_{G,\mathbf {F}'[\epsilon ]/(\epsilon ^2)}$ is an equivalence of categories
$T_{G,\mathbf {F}'[\epsilon ]/(\epsilon ^2)}$ is an equivalence of categories ![]() $\operatorname {GMod}_{\mathcal {O}_{\mathcal {E} , \mathbf {F}'[\epsilon ]/(\epsilon ^2)}}^\varphi \to \operatorname {GRep}(\mathbf {F}'[\epsilon ]/(\epsilon ^2))$ (Fact 3.2.4).
$\operatorname {GMod}_{\mathcal {O}_{\mathcal {E} , \mathbf {F}'[\epsilon ]/(\epsilon ^2)}}^\varphi \to \operatorname {GRep}(\mathbf {F}'[\epsilon ]/(\epsilon ^2))$ (Fact 3.2.4).
Corollary 6.1.12 Suppose ![]() $\mu$ is Fontaine–Laffaille and
$\mu$ is Fontaine–Laffaille and ![]() $G^{\operatorname {der}}$ is simply connected, or that
$G^{\operatorname {der}}$ is simply connected, or that ![]() $\mu$ is strongly Fontaine–Laffaille. If
$\mu$ is strongly Fontaine–Laffaille. If ![]() $Y^{\leqslant \mu }_{\mathcal {P}}(\mathbf {F}) \neq \emptyset$, then
$Y^{\leqslant \mu }_{\mathcal {P}}(\mathbf {F}) \neq \emptyset$, then ![]() $Y^{\leqslant \mu }_{\mathcal {P}} = \operatorname {Spec}(\mathbf {F})$.
$Y^{\leqslant \mu }_{\mathcal {P}} = \operatorname {Spec}(\mathbf {F})$.
6.2 Forgetting Kisin modules
Fix ![]() ${\overline {\rho }} : \Gamma _K \to G(\mathbf {F})$ and a dominant cocharacter
${\overline {\rho }} : \Gamma _K \to G(\mathbf {F})$ and a dominant cocharacter ![]() $\mu$ for
$\mu$ for ![]() $G'$. Our next goal is to show the Kisin resolution is an isomorphism in our situation.
$G'$. Our next goal is to show the Kisin resolution is an isomorphism in our situation.
Proposition 6.2.1 Let ![]() $\mathcal {P} = M_{G,\mathbf {F}}({\overline {\rho }})$, and suppose the Kisin variety
$\mathcal {P} = M_{G,\mathbf {F}}({\overline {\rho }})$, and suppose the Kisin variety ![]() $Y^{\leqslant \mu }_{\mathcal {P}}$ is trivial (i.e. isomorphic to
$Y^{\leqslant \mu }_{\mathcal {P}}$ is trivial (i.e. isomorphic to ![]() $\operatorname {Spec}(\mathbf {F})$). Then
$\operatorname {Spec}(\mathbf {F})$). Then ![]() $\Theta : X^{\mu }_{ {\overline {\rho }}} \to \operatorname {Spec} R^{\mu,\square }_{{\overline {\rho }}}$ is an isomorphism.
$\Theta : X^{\mu }_{ {\overline {\rho }}} \to \operatorname {Spec} R^{\mu,\square }_{{\overline {\rho }}}$ is an isomorphism.
Proof. Since ![]() $\Theta : X^{\leqslant \mu }_{{\overline {\rho }}} \to \operatorname {Spec} R^{\mu,\square }_{{\overline {\rho }}}$ is constructed as the limit of
$\Theta : X^{\leqslant \mu }_{{\overline {\rho }}} \to \operatorname {Spec} R^{\mu,\square }_{{\overline {\rho }}}$ is constructed as the limit of ![]() $\Theta _n : X^{\leqslant \mu }_{{\overline {\rho }}, n} \to \operatorname {Spec} R^{\mu,\square }_{{\overline {\rho }}} / \mathfrak {m}^n$ (where
$\Theta _n : X^{\leqslant \mu }_{{\overline {\rho }}, n} \to \operatorname {Spec} R^{\mu,\square }_{{\overline {\rho }}} / \mathfrak {m}^n$ (where ![]() $\mathfrak {m}$ is the maximal ideal of
$\mathfrak {m}$ is the maximal ideal of ![]() $R^{\mu,\square }_{{\overline {\rho }}}$), to check it is finite it suffices to check that each
$R^{\mu,\square }_{{\overline {\rho }}}$), to check it is finite it suffices to check that each ![]() $\Theta _n$ is finite. But
$\Theta _n$ is finite. But ![]() $R^{\mu,\square }_{{\overline {\rho }}} / \mathfrak {m}^n$ is a local Artin ring, so has a unique geometric point. As the Kisin variety is trivial, the fiber is a single point, and so
$R^{\mu,\square }_{{\overline {\rho }}} / \mathfrak {m}^n$ is a local Artin ring, so has a unique geometric point. As the Kisin variety is trivial, the fiber is a single point, and so ![]() $\Theta _n$ is quasi-finite and, hence, finite as
$\Theta _n$ is quasi-finite and, hence, finite as ![]() $\Theta$ is projective by Proposition 3.3.8. Thus,
$\Theta$ is projective by Proposition 3.3.8. Thus, ![]() $X^{\leqslant \mu }_{{\overline {\rho }}} = \operatorname {Spec} S$ for a local ring
$X^{\leqslant \mu }_{{\overline {\rho }}} = \operatorname {Spec} S$ for a local ring ![]() $S$ that is finite over
$S$ that is finite over ![]() $R^{\mu,\square }_{{\overline {\rho }}}$.
$R^{\mu,\square }_{{\overline {\rho }}}$.
As the Kisin variety is trivial, ![]() $\Theta$ induces an injection on tangent spaces at the closed point. Using the finiteness of
$\Theta$ induces an injection on tangent spaces at the closed point. Using the finiteness of ![]() $S$ and Nakayama's lemma, we see
$S$ and Nakayama's lemma, we see ![]() $\Theta$ is a closed immersion and hence
$\Theta$ is a closed immersion and hence ![]() $S$ is a quotient of
$S$ is a quotient of ![]() $R_{{\overline {\rho }}}^{\mu,\square }$. However, since
$R_{{\overline {\rho }}}^{\mu,\square }$. However, since ![]() $R_{{\overline {\rho }}}^{\mu,\square }$ injects into
$R_{{\overline {\rho }}}^{\mu,\square }$ injects into ![]() $R_{{\overline {\rho }}}^{\mu,\square }[ {1}/{p}]$ (as
$R_{{\overline {\rho }}}^{\mu,\square }[ {1}/{p}]$ (as ![]() $R_{{\overline {\rho }}}^{\mu,\square }$ is
$R_{{\overline {\rho }}}^{\mu,\square }$ is ![]() $\Lambda$-flat) and
$\Lambda$-flat) and ![]() $\Theta [ {1}/{p}]$ is an isomorphism (by Proposition 3.3.8(iii)), it follows that
$\Theta [ {1}/{p}]$ is an isomorphism (by Proposition 3.3.8(iii)), it follows that ![]() $R_{{\overline {\rho }}}^{\mu,\square } \to S$ is injective. This completes the proof.
$R_{{\overline {\rho }}}^{\mu,\square } \to S$ is injective. This completes the proof.
Corollary 6.2.2 Fix a ![]() $G$-Kisin module
$G$-Kisin module ![]() $\overline {\mathfrak {P}}$ in
$\overline {\mathfrak {P}}$ in ![]() $M_{G,\mathbf {F}}({\overline {\rho }}|_{\Gamma _\infty })$ of type
$M_{G,\mathbf {F}}({\overline {\rho }}|_{\Gamma _\infty })$ of type ![]() $\leqslant \mu$. If the Kisin variety is trivial, then
$\leqslant \mu$. If the Kisin variety is trivial, then ![]() $R_{{\overline {\rho }}}^{\mu,\square } = R_{{\overline {\rho }},\overline {\mathfrak {P}}} ^{\mu, \square,\operatorname {flat}}$.
$R_{{\overline {\rho }}}^{\mu,\square } = R_{{\overline {\rho }},\overline {\mathfrak {P}}} ^{\mu, \square,\operatorname {flat}}$.
Proof. Proposition 6.2.1 shows that ![]() $X^{\mu }_{{\overline {\rho }}}$ is represented by local ring; it is
$X^{\mu }_{{\overline {\rho }}}$ is represented by local ring; it is ![]() $\Lambda$-flat by Fact 2.4.2. Using Proposition 3.3.8(i), we see it is isomorphic to
$\Lambda$-flat by Fact 2.4.2. Using Proposition 3.3.8(i), we see it is isomorphic to ![]() $\operatorname {Spf} R^{\mu,\square,\operatorname {flat}}_{{\overline {\rho }},\overline {\mathfrak {P}}}$.
$\operatorname {Spf} R^{\mu,\square,\operatorname {flat}}_{{\overline {\rho }},\overline {\mathfrak {P}}}$.
Remark 6.2.3 We know that the Kisin variety is trivial when ![]() $G^{\operatorname {der}}$ is simply connected and
$G^{\operatorname {der}}$ is simply connected and ![]() $\mu$ is Fontaine–Laffaille, or when
$\mu$ is Fontaine–Laffaille, or when ![]() $\mu$ is strongly Fontaine–Laffaille (Corollary 6.1.12). We expect the Kisin variety to be trivial for most
$\mu$ is strongly Fontaine–Laffaille (Corollary 6.1.12). We expect the Kisin variety to be trivial for most ![]() ${\overline {\rho }}$ when
${\overline {\rho }}$ when ![]() $\mu$ is Fontaine–Laffaille, but we give an example below where the Kisin variety is non-trivial for a particular
$\mu$ is Fontaine–Laffaille, but we give an example below where the Kisin variety is non-trivial for a particular ![]() ${\overline {\rho }}$ valued in the non-simply connected group
${\overline {\rho }}$ valued in the non-simply connected group ![]() $\operatorname {PGL}_2$ and a particular
$\operatorname {PGL}_2$ and a particular ![]() $\mu$ which is Fontaine–Laffaille but not strongly Fontaine–Laffaille.
$\mu$ which is Fontaine–Laffaille but not strongly Fontaine–Laffaille.
Example 6.2.4 Let ![]() $K = \mathbf {Q}_{p}$ with
$K = \mathbf {Q}_{p}$ with ![]() $p \neq 2$, and consider the projection map
$p \neq 2$, and consider the projection map ![]() $\mathrm {pr}:\operatorname {GL}_2 \rightarrow \mathrm {PGL}_2$. Let
$\mathrm {pr}:\operatorname {GL}_2 \rightarrow \mathrm {PGL}_2$. Let ![]() $\overline {\omega }$ denote mod
$\overline {\omega }$ denote mod ![]() $p$ cyclotomic character. Consider
$p$ cyclotomic character. Consider ![]() ${\overline {\rho }} = \overline {\omega }^{ ({p-1})/{2}} \oplus 1$ and
${\overline {\rho }} = \overline {\omega }^{ ({p-1})/{2}} \oplus 1$ and ![]() ${\overline {\rho }}' = \mathrm {pr}({\overline {\rho }})$, and let
${\overline {\rho }}' = \mathrm {pr}({\overline {\rho }})$, and let ![]() $\mathcal {P}' = M_{\mathrm {PGL}_2, \mathbf {F}}({\overline {\rho }}')$. We denote the cocharacter of
$\mathcal {P}' = M_{\mathrm {PGL}_2, \mathbf {F}}({\overline {\rho }}')$. We denote the cocharacter of ![]() $\operatorname {GL}_2$ sending
$\operatorname {GL}_2$ sending ![]() $u$ to the diagonal matrix with entries
$u$ to the diagonal matrix with entries ![]() $u^a$ and
$u^a$ and ![]() $u^b$ by
$u^b$ by ![]() $(a,b)$. We abuse notation and use the same notation to denote the composition of this cocharacter with
$(a,b)$. We abuse notation and use the same notation to denote the composition of this cocharacter with ![]() $\mathrm {pr}$.
$\mathrm {pr}$.
We claim that for ![]() $\mu = ( ({p-1})/{2}, 0)$, the
$\mu = ( ({p-1})/{2}, 0)$, the ![]() $\mathrm {PGL}_2$ Kisin variety
$\mathrm {PGL}_2$ Kisin variety ![]() $Y^{\leqslant \mu }_{\mathcal {P}'}$ has at least two closed points. Note that
$Y^{\leqslant \mu }_{\mathcal {P}'}$ has at least two closed points. Note that ![]() $\mu$ is Fontaine–Laffaille but not strongly Fontaine–Laffaille, and
$\mu$ is Fontaine–Laffaille but not strongly Fontaine–Laffaille, and ![]() $\operatorname {PGL}_2$ is not simply connected. We start with the rank 2 Kisin module
$\operatorname {PGL}_2$ is not simply connected. We start with the rank 2 Kisin module ![]() $\mathfrak {M}_1$ over
$\mathfrak {M}_1$ over ![]() $\mathbf {F}$ with Frobenius given by
$\mathbf {F}$ with Frobenius given by ![]() $u^{\mu }$. Clearly
$u^{\mu }$. Clearly ![]() $\mathrm {pr}(\mathfrak {M}_1) = \mathfrak {P}'_1$ is a lattice in
$\mathrm {pr}(\mathfrak {M}_1) = \mathfrak {P}'_1$ is a lattice in ![]() $\mathcal {P}'$ with type
$\mathcal {P}'$ with type ![]() $\leqslant \mu$. We can define a second lattice
$\leqslant \mu$. We can define a second lattice ![]() $\mathfrak {M}_2$ in
$\mathfrak {M}_2$ in ![]() $\mathfrak {M}_1[1/u]$ which scales the second basis vector by
$\mathfrak {M}_1[1/u]$ which scales the second basis vector by ![]() $u$; Frobenius is then given by
$u$; Frobenius is then given by ![]() $u^{( ({p-1})/{2}, p-1)}$. The pushout
$u^{( ({p-1})/{2}, p-1)}$. The pushout ![]() $\mathrm {pr}(\mathfrak {M}_2) = \mathfrak {P}'_2$ is a lattice in
$\mathrm {pr}(\mathfrak {M}_2) = \mathfrak {P}'_2$ is a lattice in ![]() $\mathcal {P}'$ different from
$\mathcal {P}'$ different from ![]() $\mathfrak {P}_1'$ because
$\mathfrak {P}_1'$ because ![]() $u^{(0,1)} \notin L^+ \mathrm {PGL}_2(\mathbf {F})$. Finally, the image of
$u^{(0,1)} \notin L^+ \mathrm {PGL}_2(\mathbf {F})$. Finally, the image of ![]() $u^{( ({p-1})/{2}, p-1)}$ in
$u^{( ({p-1})/{2}, p-1)}$ in ![]() $\operatorname {Gr}_{\mathrm {PGL}_2}(\mathbf {F})$ is the same as the image of
$\operatorname {Gr}_{\mathrm {PGL}_2}(\mathbf {F})$ is the same as the image of ![]() $u^{( ({p-1})/{2},0)}$ and so
$u^{( ({p-1})/{2},0)}$ and so ![]() $\mathfrak {P}'_2$ has type
$\mathfrak {P}'_2$ has type ![]() $\leqslant \mu$.
$\leqslant \mu$.
6.3 Forgetting Galois representations
We next study the forgetful map ![]() $D^{\mu,\beta,\square }_{ {\overline {\rho }},\overline {\mathfrak {P}}} \to D^{\leqslant \mu,\beta,\square }_{\overline {\mathfrak {P}}}$. To do so, we use the theory of
$D^{\mu,\beta,\square }_{ {\overline {\rho }},\overline {\mathfrak {P}}} \to D^{\leqslant \mu,\beta,\square }_{\overline {\mathfrak {P}}}$. To do so, we use the theory of ![]() $(\varphi,\widehat {\Gamma })$-modules with
$(\varphi,\widehat {\Gamma })$-modules with ![]() $G$-structure developed in [Reference LevinLev15, § 4.2], extending Liu's theory of
$G$-structure developed in [Reference LevinLev15, § 4.2], extending Liu's theory of ![]() $(\varphi,\widehat {G})$-modules (see [Reference LiuLiu10]). We briefly recall a concrete version here.
$(\varphi,\widehat {G})$-modules (see [Reference LiuLiu10]). We briefly recall a concrete version here.
Let ![]() $\mathcal {O}_{\overline {K}}^\flat$ be the perfection of
$\mathcal {O}_{\overline {K}}^\flat$ be the perfection of ![]() $\mathcal {O}_{\overline {K}} / (p)$ and
$\mathcal {O}_{\overline {K}} / (p)$ and ![]() $\mathbf {A}_{{\operatorname {inf}}} = W(\mathcal {O}_{\overline {K}}^\flat )$. A fixed compatible set
$\mathbf {A}_{{\operatorname {inf}}} = W(\mathcal {O}_{\overline {K}}^\flat )$. A fixed compatible set ![]() $\{p^{1/p}, p^{1/p^2}, \ldots \}$ of
$\{p^{1/p}, p^{1/p^2}, \ldots \}$ of ![]() $p$-power roots of
$p$-power roots of ![]() $p$ defines an element
$p$ defines an element ![]() $\pi \in \mathcal {O}_{\overline {K}}^\flat$. Let
$\pi \in \mathcal {O}_{\overline {K}}^\flat$. Let ![]() $[\pi ] \in \mathbf {A}_{{\operatorname {inf}}}$ be the Teichmuller lift of
$[\pi ] \in \mathbf {A}_{{\operatorname {inf}}}$ be the Teichmuller lift of ![]() $\pi$. There are embeddings
$\pi$. There are embeddings ![]() $\mathfrak {S} \hookrightarrow \mathbf {A}_{{\operatorname {inf}}}$ and
$\mathfrak {S} \hookrightarrow \mathbf {A}_{{\operatorname {inf}}}$ and ![]() $\mathcal {O}_{\mathcal {E}} \hookrightarrow \mathbf {A}_{{\operatorname {inf}}}$ defined by sending
$\mathcal {O}_{\mathcal {E}} \hookrightarrow \mathbf {A}_{{\operatorname {inf}}}$ defined by sending ![]() $u \in \mathfrak {S}$ to
$u \in \mathfrak {S}$ to ![]() $[\pi ]$; they are compatible with Frobenius. In this section only, let
$[\pi ]$; they are compatible with Frobenius. In this section only, let ![]() $\mathfrak {t} \in \mathbf {A}_{{\operatorname {inf}}}$ denote the period of
$\mathfrak {t} \in \mathbf {A}_{{\operatorname {inf}}}$ denote the period of ![]() $\mathfrak {S}(1)$, which satisfies
$\mathfrak {S}(1)$, which satisfies ![]() $\varphi (\mathfrak {t}) = c_0^{-1} E(u) \mathfrak {t}$.
$\varphi (\mathfrak {t}) = c_0^{-1} E(u) \mathfrak {t}$.
The theory of ![]() $(\varphi,\widehat {G})$-modules uses a ring
$(\varphi,\widehat {G})$-modules uses a ring ![]() $\widehat {R} \subset \mathbf {A}_{{\operatorname {inf}}}$ which contains
$\widehat {R} \subset \mathbf {A}_{{\operatorname {inf}}}$ which contains ![]() $\mathfrak {S}$. It is defined on p. 5 of [Reference LiuLiu10]; we do not need detailed information about it. For a
$\mathfrak {S}$. It is defined on p. 5 of [Reference LiuLiu10]; we do not need detailed information about it. For a ![]() $\mathbf {Z}_p$-algebra
$\mathbf {Z}_p$-algebra ![]() $A$, define
$A$, define ![]() $\widehat {R}_A := \widehat {R} \otimes _{\mathbf {Z}_p} A$ and
$\widehat {R}_A := \widehat {R} \otimes _{\mathbf {Z}_p} A$ and ![]() $\mathbf {A}_{{\operatorname {inf}},A} := \mathbf {A}_{{\operatorname {inf}}} \otimes _{\mathbf {Z}_p} A$.
$\mathbf {A}_{{\operatorname {inf}},A} := \mathbf {A}_{{\operatorname {inf}}} \otimes _{\mathbf {Z}_p} A$.
As in § 1.3.4, let ![]() $K_\infty = K(p^{1/p}, p^{1/p^2}, \ldots )$ and
$K_\infty = K(p^{1/p}, p^{1/p^2}, \ldots )$ and ![]() $\Gamma _\infty = \operatorname {Gal}(\overline {K} / K_\infty )$. Furthermore, set
$\Gamma _\infty = \operatorname {Gal}(\overline {K} / K_\infty )$. Furthermore, set ![]() $K_{p^\infty } = \cup _n K(\zeta _{p^n})$ where
$K_{p^\infty } = \cup _n K(\zeta _{p^n})$ where ![]() $\zeta _{p^n}$ is a primitive
$\zeta _{p^n}$ is a primitive ![]() $p^n$th root of unity. Let
$p^n$th root of unity. Let ![]() $K_{\infty,p^\infty }$ denote the compositum of
$K_{\infty,p^\infty }$ denote the compositum of ![]() $K_\infty$ and
$K_\infty$ and ![]() $K_{p^\infty }$. It is Galois over
$K_{p^\infty }$. It is Galois over ![]() $K$; set
$K$; set ![]() $\widehat {\Gamma } := \operatorname {Gal}(K_{\infty, p^\infty } /K)$ and
$\widehat {\Gamma } := \operatorname {Gal}(K_{\infty, p^\infty } /K)$ and ![]() $\widehat {\Gamma }_\infty := \operatorname {Gal}(K_{\infty,p^\infty }/K_\infty )$.
$\widehat {\Gamma }_\infty := \operatorname {Gal}(K_{\infty,p^\infty }/K_\infty )$.
Fix a coefficient ring ![]() $A \in \widehat {\mathcal {C}}_{\Lambda }$.
$A \in \widehat {\mathcal {C}}_{\Lambda }$.
Definition 6.3.1 Define ![]() $G_A(u^n)$ to be the kernel of the reduction map
$G_A(u^n)$ to be the kernel of the reduction map
For our purposes, we do not need the general definition of a ![]() $(\varphi,\widehat {\Gamma })$-modules with
$(\varphi,\widehat {\Gamma })$-modules with ![]() $G$-structure [Reference LevinLev15, Definition 4.2.6], and instead use the following description [Reference LevinLev15, Proposition 4.3.10].
$G$-structure [Reference LevinLev15, Definition 4.2.6], and instead use the following description [Reference LevinLev15, Proposition 4.3.10].
Fact 6.3.2 A crystalline ![]() $(\varphi,\widehat {\Gamma })$-module with
$(\varphi,\widehat {\Gamma })$-module with ![]() $G$-structure and coefficients in
$G$-structure and coefficients in ![]() $A$ is equivalent to a
$A$ is equivalent to a ![]() $G$-Kisin module
$G$-Kisin module ![]() $(\mathfrak {P},\phi )$ with coefficients in
$(\mathfrak {P},\phi )$ with coefficients in ![]() $A$ with a ‘crystalline
$A$ with a ‘crystalline ![]() $\widehat {\Gamma }$-structure’. If we fix a trivialization
$\widehat {\Gamma }$-structure’. If we fix a trivialization ![]() $\beta$ of
$\beta$ of ![]() $\mathfrak {P}$, trivialize
$\mathfrak {P}$, trivialize ![]() $\varphi ^*(\mathfrak {P})$ using
$\varphi ^*(\mathfrak {P})$ using ![]() $1 \otimes _{\varphi } \beta$, and let
$1 \otimes _{\varphi } \beta$, and let ![]() $C_{\mathfrak {P}, \beta } \in G(\mathfrak {S}_{A}[ 1 / E(u)])$ correspond to
$C_{\mathfrak {P}, \beta } \in G(\mathfrak {S}_{A}[ 1 / E(u)])$ correspond to ![]() $\varphi$, a crystalline
$\varphi$, a crystalline ![]() $\widehat {\Gamma }$-structure is a continuous map
$\widehat {\Gamma }$-structure is a continuous map
that satisfies the following conditions:
(i)
 $C_{\mathfrak {P}, \beta } \varphi (B_\gamma ) = B_\gamma \cdot \gamma (C_{\mathfrak {P}, \beta })$ in
$C_{\mathfrak {P}, \beta } \varphi (B_\gamma ) = B_\gamma \cdot \gamma (C_{\mathfrak {P}, \beta })$ in  $G(\mathbf {A}_{{\operatorname {inf}},A})$ for all
$G(\mathbf {A}_{{\operatorname {inf}},A})$ for all  $\gamma \in \widehat {\Gamma }$;
$\gamma \in \widehat {\Gamma }$;(ii)
 $B_\gamma = \operatorname {Id}$ for all
$B_\gamma = \operatorname {Id}$ for all  $\gamma \in \widehat {\Gamma }_\infty$;
$\gamma \in \widehat {\Gamma }_\infty$;(iii)
 $B_\gamma \in G_A(u^p)$ for all
$B_\gamma \in G_A(u^p)$ for all  $\gamma \in \widehat {\Gamma }$;
$\gamma \in \widehat {\Gamma }$;(iv)
 $B_{\gamma \gamma '} = B_\gamma \cdot \gamma (B_{\gamma '})$ for all
$B_{\gamma \gamma '} = B_\gamma \cdot \gamma (B_{\gamma '})$ for all  $\gamma, \gamma ' \in \widehat {\Gamma }$.
$\gamma, \gamma ' \in \widehat {\Gamma }$.
Fact 6.3.3 Let ![]() $A$ be a finite
$A$ be a finite ![]() $\Lambda$-algebra which is either flat or Artinian. There is a functor
$\Lambda$-algebra which is either flat or Artinian. There is a functor ![]() $\widehat {T}_{G,A}$ from the category of crystalline
$\widehat {T}_{G,A}$ from the category of crystalline ![]() $(\varphi,\widehat {\Gamma })$-modules with
$(\varphi,\widehat {\Gamma })$-modules with ![]() $G$-structure with coefficients in
$G$-structure with coefficients in ![]() $A$ to
$A$ to ![]() $\operatorname {GRep}_A(\Gamma _K)$. It is compatible with base change along finite flat maps. For a crystalline
$\operatorname {GRep}_A(\Gamma _K)$. It is compatible with base change along finite flat maps. For a crystalline ![]() $(\varphi,\widehat {\Gamma })$-module
$(\varphi,\widehat {\Gamma })$-module ![]() $\widehat {\mathfrak {P}}$ with
$\widehat {\mathfrak {P}}$ with ![]() $G$-structure and underlying
$G$-structure and underlying ![]() $G$-Kisin module
$G$-Kisin module ![]() $\mathfrak {P}$, there is a natural isomorphism
$\mathfrak {P}$, there is a natural isomorphism
where ![]() $\widetilde {T}_{G,A}$ is the functor from
$\widetilde {T}_{G,A}$ is the functor from ![]() $G$-Kisin modules to representations of
$G$-Kisin modules to representations of ![]() $\Gamma _\infty$ in Definition 3.2.5.
$\Gamma _\infty$ in Definition 3.2.5.
Proof. The functor ![]() $\widehat {T}_{G,A}$ is discussed in [Reference LevinLev15, § 4.2].
$\widehat {T}_{G,A}$ is discussed in [Reference LevinLev15, § 4.2].
Remark 6.3.4 As the name suggests, crystalline ![]() $(\varphi,\widehat {\Gamma })$-modules with
$(\varphi,\widehat {\Gamma })$-modules with ![]() $G$-structure are related to crystalline representations. Let
$G$-structure are related to crystalline representations. Let ![]() $L'/L$ be a finite extension with ring of integer
$L'/L$ be a finite extension with ring of integer ![]() $\mathcal {O}_{L'}$. Then
$\mathcal {O}_{L'}$. Then ![]() $\widehat {T}_{G,\mathcal {O}_{L'}}$ gives an equivalence of categories between the category of crystalline
$\widehat {T}_{G,\mathcal {O}_{L'}}$ gives an equivalence of categories between the category of crystalline ![]() $(\varphi,\widehat {\Gamma })$-modules with
$(\varphi,\widehat {\Gamma })$-modules with ![]() $G$-structure and coefficients in
$G$-structure and coefficients in ![]() $\mathcal {O}_{L'}$ and the category of crystalline representations in
$\mathcal {O}_{L'}$ and the category of crystalline representations in ![]() $\operatorname {GRep}_{\mathcal {O}_{L'}}(\Gamma _K)$. This is [Reference LevinLev15, Proposition 4.3.5].
$\operatorname {GRep}_{\mathcal {O}_{L'}}(\Gamma _K)$. This is [Reference LevinLev15, Proposition 4.3.5].
We say that ![]() $C \in G(\mathfrak {S}_A[1/E(u)])$ has height in
$C \in G(\mathfrak {S}_A[1/E(u)])$ has height in ![]() $[a,b]$ with respect to the adjoint representation if
$[a,b]$ with respect to the adjoint representation if
Lemma 6.3.5 Let ![]() $A$ be a
$A$ be a ![]() $p$-adically complete
$p$-adically complete ![]() $\Lambda$-algebra such that
$\Lambda$-algebra such that ![]() $p A =0$, and let
$p A =0$, and let ![]() $C \in G(\mathfrak {S}_A [ 1 / E(u)])$ have height in
$C \in G(\mathfrak {S}_A [ 1 / E(u)])$ have height in ![]() $[-h,h]$ with respect to the adjoint representation. If
$[-h,h]$ with respect to the adjoint representation. If ![]() $h < p-1$, then for any
$h < p-1$, then for any ![]() $Y \in G_A(u^n)$ with
$Y \in G_A(u^n)$ with ![]() $n \geqslant p$, we have
$n \geqslant p$, we have
Proof. Let ![]() $\mathcal {O}_G$ denote the coordinate ring of
$\mathcal {O}_G$ denote the coordinate ring of ![]() $G$ and let
$G$ and let ![]() $I_e$ denote the ideal defining the identity. We have that
$I_e$ denote the ideal defining the identity. We have that ![]() $\mathcal {O}_G/I_e = \Lambda$ and
$\mathcal {O}_G/I_e = \Lambda$ and ![]() $I_e / I_e^2 \simeq (\operatorname {Lie} G)^\vee$. For a
$I_e / I_e^2 \simeq (\operatorname {Lie} G)^\vee$. For a ![]() $\Lambda$-algebra
$\Lambda$-algebra ![]() $B$, we know that
$B$, we know that ![]() $G(B)$ can be identified with maps of rings from
$G(B)$ can be identified with maps of rings from ![]() $\mathcal {O}_G$ to
$\mathcal {O}_G$ to ![]() $B$; the identity of
$B$; the identity of ![]() $G(B)$ is the natural map
$G(B)$ is the natural map ![]() $\mathcal {O}_G \to \mathcal {O}_G/ I_e = \Lambda \to B$. Thus, we can identify
$\mathcal {O}_G \to \mathcal {O}_G/ I_e = \Lambda \to B$. Thus, we can identify ![]() $G_A(u^n)$ with
$G_A(u^n)$ with
Note that ![]() $\varphi (Y)$ is the composition of
$\varphi (Y)$ is the composition of ![]() $Y$ with the endomorphism
$Y$ with the endomorphism ![]() $\varphi$ of
$\varphi$ of ![]() $\mathbf {A}_{{\operatorname {inf}},A}$, so, in particular, we conclude that
$\mathbf {A}_{{\operatorname {inf}},A}$, so, in particular, we conclude that ![]() $\varphi (Y)(I_e) \subset (\varphi (\varphi (\mathfrak {t}) u^n)) = (\varphi (\varphi (\mathfrak {t})) u^{pn})$.
$\varphi (Y)(I_e) \subset (\varphi (\varphi (\mathfrak {t}) u^n)) = (\varphi (\varphi (\mathfrak {t})) u^{pn})$.
Now conjugation by ![]() $C$ induces an automorphism of
$C$ induces an automorphism of ![]() $G_{\mathfrak {S}_A[1/E(u)]}$, and hence an automorphism
$G_{\mathfrak {S}_A[1/E(u)]}$, and hence an automorphism
Conjugation by ![]() $\varphi (C)$ likewise induces an automorphism, and is given by
$\varphi (C)$ likewise induces an automorphism, and is given by ![]() $(1 \otimes \varphi ) \circ \operatorname {Ad}_{\mathcal {O}_G}(C)^*$. For
$(1 \otimes \varphi ) \circ \operatorname {Ad}_{\mathcal {O}_G}(C)^*$. For ![]() $x \in I_e \otimes 1$, we claim that
$x \in I_e \otimes 1$, we claim that
By successive approximation, we can just study the induced automorphisms of the graded pieces ![]() $I_e^j / I_e^{j+1} \otimes _{\Lambda } \mathfrak {S}_A[1/E(u)] \simeq \operatorname {Sym}^j(\operatorname {Lie}(G)^\vee ) \otimes _{\Lambda } \mathfrak {S}_A[1/E(u)]$. Using the height condition, the image of
$I_e^j / I_e^{j+1} \otimes _{\Lambda } \mathfrak {S}_A[1/E(u)] \simeq \operatorname {Sym}^j(\operatorname {Lie}(G)^\vee ) \otimes _{\Lambda } \mathfrak {S}_A[1/E(u)]$. Using the height condition, the image of ![]() $\operatorname {Sym}^j(\operatorname {Lie}(G)^\vee ) \otimes _{\Lambda } \mathfrak {S}_A[1/E(u)]$ lies in
$\operatorname {Sym}^j(\operatorname {Lie}(G)^\vee ) \otimes _{\Lambda } \mathfrak {S}_A[1/E(u)]$ lies in ![]() $E(u) ^{-h j} \operatorname {Sym}^j(\operatorname {Lie}(G)^\vee ) \otimes _{\Lambda } \mathfrak {S}_A[1/E(u)]$ as desired.
$E(u) ^{-h j} \operatorname {Sym}^j(\operatorname {Lie}(G)^\vee ) \otimes _{\Lambda } \mathfrak {S}_A[1/E(u)]$ as desired.
Now viewing ![]() $\varphi (C) \varphi (Y) \varphi (C)^{-1}$ as a homomorphism from
$\varphi (C) \varphi (Y) \varphi (C)^{-1}$ as a homomorphism from ![]() $\mathcal {O}_G \otimes _{\Lambda } \mathfrak {S}_A[1/E(u)]$ to
$\mathcal {O}_G \otimes _{\Lambda } \mathfrak {S}_A[1/E(u)]$ to ![]() $\mathbf {A}_{{\operatorname {inf}},A} \otimes _{\Lambda } \mathfrak {S}_A[1/E(u)]$, observe that for
$\mathbf {A}_{{\operatorname {inf}},A} \otimes _{\Lambda } \mathfrak {S}_A[1/E(u)]$, observe that for ![]() $x \in I_e \otimes 1$
$x \in I_e \otimes 1$
Using (6.3.1), as ![]() $\varphi (Y)(I_e^j) \subset \varphi (\varphi (\mathfrak {t}) )^j u ^{pn j}$ we see that
$\varphi (Y)(I_e^j) \subset \varphi (\varphi (\mathfrak {t}) )^j u ^{pn j}$ we see that
Thus, to check that ![]() $\varphi (C) \varphi (Y) \varphi (C)^{-1} \in G_A(u^{n+1})$, it suffices to check that
$\varphi (C) \varphi (Y) \varphi (C)^{-1} \in G_A(u^{n+1})$, it suffices to check that ![]() $u^{n+1} \varphi (\mathfrak {t})$ divides
$u^{n+1} \varphi (\mathfrak {t})$ divides ![]() $\alpha _j := \varphi (\varphi (\mathfrak {t}) )^j u ^{pn j} \varphi (E(u))^{-h j}$ in
$\alpha _j := \varphi (\varphi (\mathfrak {t}) )^j u ^{pn j} \varphi (E(u))^{-h j}$ in ![]() $\mathbf {A}_{{\operatorname {inf}},A}$ for any
$\mathbf {A}_{{\operatorname {inf}},A}$ for any ![]() $j \geqslant 1$. As
$j \geqslant 1$. As ![]() $p A =0$ we have that
$p A =0$ we have that ![]() $E(u) = u$, so using that
$E(u) = u$, so using that ![]() $\mathfrak {t} E(u)$ divides
$\mathfrak {t} E(u)$ divides ![]() $\varphi (\mathfrak {t})$ in
$\varphi (\mathfrak {t})$ in ![]() $\mathbf {A}_{{\operatorname {inf}}}$ (since
$\mathbf {A}_{{\operatorname {inf}}}$ (since ![]() $\varphi (\mathfrak {t}) = c_0^{-1} E(u) \mathfrak {t}$) we see that
$\varphi (\mathfrak {t}) = c_0^{-1} E(u) \mathfrak {t}$) we see that ![]() $\alpha _j$ is a multiple of
$\alpha _j$ is a multiple of ![]() $\varphi (\mathfrak {t}) u^{pj} u^{pn j} u^{-p h j}$. However, when
$\varphi (\mathfrak {t}) u^{pj} u^{pn j} u^{-p h j}$. However, when ![]() $h < p-1$ and
$h < p-1$ and ![]() $n \geqslant p$,
$n \geqslant p$, ![]() $(p-1)n \geqslant p (p-1) > p (h-1)$ and, hence,
$(p-1)n \geqslant p (p-1) > p (h-1)$ and, hence, ![]() $(p + pn - p h)j > n$ as desired.
$(p + pn - p h)j > n$ as desired.
Lemma 6.3.6 Suppose ![]() $A$ is a
$A$ is a ![]() $p$-adically complete
$p$-adically complete ![]() $\Lambda$-algebra such that
$\Lambda$-algebra such that ![]() $p A=0$. For
$p A=0$. For ![]() $\mathfrak {P} \in D_{\overline {\mathfrak {P}}}^{\leqslant \mu,\beta } (A)$ with
$\mathfrak {P} \in D_{\overline {\mathfrak {P}}}^{\leqslant \mu,\beta } (A)$ with ![]() $\mu$ in the Fontaine–Laffaille range, there is at most one crystalline
$\mu$ in the Fontaine–Laffaille range, there is at most one crystalline ![]() $\widehat {\Gamma }$-structure on
$\widehat {\Gamma }$-structure on ![]() $\mathfrak {P}$.
$\mathfrak {P}$.
Proof. Suppose we have two crystalline ![]() $\widehat {\Gamma }$-structures, with the action of
$\widehat {\Gamma }$-structures, with the action of ![]() $\gamma \in \widehat {\Gamma }$ given by
$\gamma \in \widehat {\Gamma }$ given by ![]() $B_\gamma$ and
$B_\gamma$ and ![]() $B'_\gamma$ in
$B'_\gamma$ in ![]() $G(\mathbf {A}_{{\operatorname {inf}},A})$. Using property (iii) of Fact 6.3.2, we have that
$G(\mathbf {A}_{{\operatorname {inf}},A})$. Using property (iii) of Fact 6.3.2, we have that ![]() $B_\gamma (B'_\gamma )^{-1} \in G_A(u^p)$. Furthermore, if the Frobenius on
$B_\gamma (B'_\gamma )^{-1} \in G_A(u^p)$. Furthermore, if the Frobenius on ![]() $\mathfrak {P}$ is given by
$\mathfrak {P}$ is given by ![]() $C$, then
$C$, then
An inductive argument using Lemma 6.3.5 shows that ![]() $B_\gamma (B'_\gamma )^{-1} \in G_A(u^n)$ for all
$B_\gamma (B'_\gamma )^{-1} \in G_A(u^n)$ for all ![]() $n \geqslant p$. Thus,
$n \geqslant p$. Thus, ![]() $B_\gamma = B_\gamma '$ as desired.
$B_\gamma = B_\gamma '$ as desired.
Note the forgetful map ![]() $\operatorname {Spf} R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\beta,\square } \to \operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu,\beta,\square }$ factors through the flat closure by Lemma 3.3.4.
$\operatorname {Spf} R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\beta,\square } \to \operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu,\beta,\square }$ factors through the flat closure by Lemma 3.3.4.
Proposition 6.3.7 For ![]() $\mu$ in the Fontaine–Laffaille range, the natural map
$\mu$ in the Fontaine–Laffaille range, the natural map ![]() $\operatorname {Spf} R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\beta,\square,\operatorname {flat}} \to \operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu,\beta,\square }$ is injective on tangent spaces.
$\operatorname {Spf} R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\beta,\square,\operatorname {flat}} \to \operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu,\beta,\square }$ is injective on tangent spaces.
Proof. Let ![]() $A$ be a finite
$A$ be a finite ![]() $\mathbf {F}$-algebra, and set
$\mathbf {F}$-algebra, and set ![]() $R:= R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\beta,\square,\operatorname {flat}}$. We first claim that for every
$R:= R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\beta,\square,\operatorname {flat}}$. We first claim that for every ![]() $A$-valued point
$A$-valued point ![]() $f_A : R \to A$, there exists a finite flat
$f_A : R \to A$, there exists a finite flat ![]() $\Lambda$-algebra
$\Lambda$-algebra ![]() $B$ and a
$B$ and a ![]() $B$-valued point
$B$-valued point ![]() $f_B : R \to B$ that lifts
$f_B : R \to B$ that lifts ![]() $f_A$. We do so using an idea from [Reference BartlettBar21, Lemma 3.2.2]. Note that
$f_A$. We do so using an idea from [Reference BartlettBar21, Lemma 3.2.2]. Note that ![]() $R$ is a complete local
$R$ is a complete local ![]() $\Lambda$-algebra that is reduced and
$\Lambda$-algebra that is reduced and ![]() $\Lambda$-flat (Corollary 6.2.2 and Fact 2.4.2). Furthermore,
$\Lambda$-flat (Corollary 6.2.2 and Fact 2.4.2). Furthermore, ![]() $R$ is Nagata as it is a complete local Noetherian ring. Now
$R$ is Nagata as it is a complete local Noetherian ring. Now ![]() $f_A : R \to A$ factors through
$f_A : R \to A$ factors through ![]() $R/ \mathfrak {m}_R^j$ for some integer
$R/ \mathfrak {m}_R^j$ for some integer ![]() $j \geqslant 1$ by continuity, so we easily adapt [Reference BartlettBar20, Lemma 4.1.2] to find a finite flat
$j \geqslant 1$ by continuity, so we easily adapt [Reference BartlettBar20, Lemma 4.1.2] to find a finite flat ![]() $\Lambda$-algebra
$\Lambda$-algebra ![]() $B$ and a
$B$ and a ![]() $B$-valued point
$B$-valued point ![]() $f_B : R \to B$ that lifts
$f_B : R \to B$ that lifts ![]() $f_A$.
$f_A$.
We apply the previous paragraph with ![]() $A = \mathbf {F}[\epsilon ]/(\epsilon ^2)$. A tangent vector to
$A = \mathbf {F}[\epsilon ]/(\epsilon ^2)$. A tangent vector to ![]() $\operatorname {Spf} R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\beta,\square,\operatorname {flat}}$ at the closed point corresponds to a pair
$\operatorname {Spf} R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\beta,\square,\operatorname {flat}}$ at the closed point corresponds to a pair ![]() $(\mathfrak {P}_A, \rho _A)$ and is the reduction of a
$(\mathfrak {P}_A, \rho _A)$ and is the reduction of a ![]() $B$-valued point for some finite flat
$B$-valued point for some finite flat ![]() $\Lambda$-algebra
$\Lambda$-algebra ![]() $B$. This point gives a trivialized Kisin module
$B$. This point gives a trivialized Kisin module ![]() $\mathfrak {P}_B$ and a Galois representation
$\mathfrak {P}_B$ and a Galois representation ![]() $\rho : \Gamma _K \to G(B)$ such that
$\rho : \Gamma _K \to G(B)$ such that ![]() $\widetilde {T}_{G,B}(\mathfrak {P}_B) = \rho |_{\Gamma _\infty }$ and
$\widetilde {T}_{G,B}(\mathfrak {P}_B) = \rho |_{\Gamma _\infty }$ and ![]() $\rho \otimes L$ is crystalline. The same argument used in the proof of [Reference LevinLev15, Theorem 4.2.7] which relies on [Reference LiuLiu10] shows that
$\rho \otimes L$ is crystalline. The same argument used in the proof of [Reference LevinLev15, Theorem 4.2.7] which relies on [Reference LiuLiu10] shows that ![]() $\mathfrak {P}_B$ admits a crystalline
$\mathfrak {P}_B$ admits a crystalline ![]() $(\varphi,\widehat {\Gamma })$-structure
$(\varphi,\widehat {\Gamma })$-structure ![]() $\widehat {\mathfrak {P}}_B$ such that
$\widehat {\mathfrak {P}}_B$ such that ![]() $\widehat {T}_{G, B}(\widehat {\mathfrak {P}}_B) = \rho$. (In fact, as
$\widehat {T}_{G, B}(\widehat {\mathfrak {P}}_B) = \rho$. (In fact, as ![]() $B$ is finite flat it is the unique such structure.) Therefore, its reduction, the
$B$ is finite flat it is the unique such structure.) Therefore, its reduction, the ![]() $G$-Kisin module
$G$-Kisin module ![]() $\mathfrak {P}_A$, also admits a crystalline
$\mathfrak {P}_A$, also admits a crystalline ![]() $(\varphi,\widehat {\Gamma })$-structure such that
$(\varphi,\widehat {\Gamma })$-structure such that ![]() $\widehat {T}_{G, A}(\mathfrak {P}_A) = \rho _A$.
$\widehat {T}_{G, A}(\mathfrak {P}_A) = \rho _A$.
Finally, given two tangent vectors to ![]() $\operatorname {Spf} R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\beta,\square,\operatorname {flat}}$ with the same underlying
$\operatorname {Spf} R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\beta,\square,\operatorname {flat}}$ with the same underlying ![]() $G$-Kisin module, we know each admits a crystalline
$G$-Kisin module, we know each admits a crystalline ![]() $(\varphi,\widehat {\Gamma })$-structure. By Lemma 6.3.6 these structures are the same, and we know the crystalline structure determines the Galois representation.
$(\varphi,\widehat {\Gamma })$-structure. By Lemma 6.3.6 these structures are the same, and we know the crystalline structure determines the Galois representation.
Corollary 6.3.8 If ![]() $\mu$ is Fontaine–Laffaille, the natural map
$\mu$ is Fontaine–Laffaille, the natural map ![]() $\operatorname {Spf} R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\beta,\square,\operatorname {flat}} \to \operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu,\beta,\square }$ is a closed immersion.
$\operatorname {Spf} R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\beta,\square,\operatorname {flat}} \to \operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu,\beta,\square }$ is a closed immersion.
Proof. This follows from Proposition 6.3.7 and Nakayama's lemma.
6.4 Relationships between deformation rings
Definition 6.4.1 We let ![]() $R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta,\square,\nabla }$ be the
$R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta,\square,\nabla }$ be the ![]() $\Lambda$-flat and reduced quotient of
$\Lambda$-flat and reduced quotient of ![]() $R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta,\square }$ such that
$R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta,\square }$ such that ![]() $\operatorname {Spec} R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta,\square,\nabla } [1/p]$ is the vanishing locus of the monodromy condition on
$\operatorname {Spec} R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta,\square,\nabla } [1/p]$ is the vanishing locus of the monodromy condition on ![]() $\operatorname {Spec} R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta,\square }[1/p]$. Define
$\operatorname {Spec} R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta,\square }[1/p]$. Define ![]() $R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta,\nabla }$ similarly.
$R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta,\nabla }$ similarly.
There are closed immersions
As ![]() $R_{\overline {\rho }}^{\mu,\square }$ is
$R_{\overline {\rho }}^{\mu,\square }$ is ![]() $\Lambda$-flat (recall Fact 2.4.2), the forgetful map
$\Lambda$-flat (recall Fact 2.4.2), the forgetful map ![]() $\operatorname {Spf} R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\square } \to \operatorname {Spf} R_{\overline {\rho }}^{\mu,\square }$ factors through
$\operatorname {Spf} R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\square } \to \operatorname {Spf} R_{\overline {\rho }}^{\mu,\square }$ factors through ![]() $R^{\mu,\square,\operatorname {flat}}_{{\overline {\rho }},\overline {\mathfrak {P}}}$. As
$R^{\mu,\square,\operatorname {flat}}_{{\overline {\rho }},\overline {\mathfrak {P}}}$. As ![]() $\operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta, \square }$ is
$\operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta, \square }$ is ![]() $\Lambda$-flat by Lemma 3.3.4, we likewise obtain a map
$\Lambda$-flat by Lemma 3.3.4, we likewise obtain a map ![]() $\operatorname {Spf} R^{\mu,\beta,\square,\operatorname {flat}}_{{\overline {\rho }},\overline {\mathfrak {P}}} \to \operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta, \square }$.
$\operatorname {Spf} R^{\mu,\beta,\square,\operatorname {flat}}_{{\overline {\rho }},\overline {\mathfrak {P}}} \to \operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta, \square }$.
Theorem 6.4.2 Assume that ![]() $p \nmid \# \pi _1(G^{\mathrm {ad}})$ and that
$p \nmid \# \pi _1(G^{\mathrm {ad}})$ and that ![]() $\mu$ is Fontaine–Laffaille. We continue to fix a
$\mu$ is Fontaine–Laffaille. We continue to fix a ![]() $G$-Kisin module
$G$-Kisin module ![]() $\overline {\mathfrak {P}}$ over
$\overline {\mathfrak {P}}$ over ![]() $\mathbf {F}$ and a continuous Galois representation
$\mathbf {F}$ and a continuous Galois representation ![]() ${\overline {\rho }}: \Gamma _K \to G(\mathbf {F})$ together with an isomorphism
${\overline {\rho }}: \Gamma _K \to G(\mathbf {F})$ together with an isomorphism ![]() $\widetilde {T}_{G,\mathbf {F}}(\overline {\mathfrak {P}}) \simeq {\overline {\rho }}|_{\Gamma _\infty }$. If the Kisin variety
$\widetilde {T}_{G,\mathbf {F}}(\overline {\mathfrak {P}}) \simeq {\overline {\rho }}|_{\Gamma _\infty }$. If the Kisin variety ![]() $Y^{\leqslant \mu }_{M_{G,\mathbf {F}}({\overline {\rho }})}$ is trivial, there is a commutative diagram of formal schemes
$Y^{\leqslant \mu }_{M_{G,\mathbf {F}}({\overline {\rho }})}$ is trivial, there is a commutative diagram of formal schemes

with the indicated arrows isomorphisms and closed immersions, and with the arrows labeled ![]() $f.s.$ formally smooth. The square is cartesian.
$f.s.$ formally smooth. The square is cartesian.
Remark 6.4.3 The hypothesis that ![]() $p \nmid \# \pi _1(G^{\mathrm {ad}})$ is equivalent to
$p \nmid \# \pi _1(G^{\mathrm {ad}})$ is equivalent to ![]() $Z^{\operatorname {der}}$ being étale over
$Z^{\operatorname {der}}$ being étale over ![]() $\Lambda$ and
$\Lambda$ and ![]() $p \nmid \pi _1(G^{\operatorname {der}})$, which are necessary to apply many of our results. The restrictions ultimately trace back to Theorem 2.3.1 and Proposition 5.1.1.
$p \nmid \pi _1(G^{\operatorname {der}})$, which are necessary to apply many of our results. The restrictions ultimately trace back to Theorem 2.3.1 and Proposition 5.1.1.
Proof. The maps in (6.4.1) labeled ![]() $f.s.$ come from forgetting a trivialization modulo
$f.s.$ come from forgetting a trivialization modulo ![]() $E(u)^N$ of a
$E(u)^N$ of a ![]() $G$-Kisin module, or forgetting a trivialization of a Galois representation. These are formally smooth as the set of trivializations are a
$G$-Kisin module, or forgetting a trivialization of a Galois representation. These are formally smooth as the set of trivializations are a ![]() $G$-torsor and
$G$-torsor and ![]() $G$ is smooth.
$G$ is smooth.
The horizontal isomorphism comes from forgetting the ![]() $G$-Kisin module; Corollary 6.2.2 shows it is an isomorphism.
$G$-Kisin module; Corollary 6.2.2 shows it is an isomorphism.
Corollary 6.3.8 shows that the forgetful map ![]() $\operatorname {Spf} R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\beta,\square,\operatorname {flat}} \to \operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu,\beta,\square }$ is a closed immersion.
$\operatorname {Spf} R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\beta,\square,\operatorname {flat}} \to \operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu,\beta,\square }$ is a closed immersion.
We next claim that forgetful map ![]() $\operatorname {Spf} R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\beta,\square } \to \operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu,\beta,\square }$ factors through
$\operatorname {Spf} R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\beta,\square } \to \operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu,\beta,\square }$ factors through ![]() $\operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta,\square,\nabla }$ and that
$\operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta,\square,\nabla }$ and that ![]() $\imath : \operatorname {Spf} R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\beta,\square } \to \operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta,\square,\nabla }$ is a closed immersion. It suffices to check this on
$\imath : \operatorname {Spf} R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\beta,\square } \to \operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta,\square,\nabla }$ is a closed immersion. It suffices to check this on ![]() $\overline {L}$-points as
$\overline {L}$-points as ![]() $R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\beta,\square,\operatorname {flat}}$ and
$R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\beta,\square,\operatorname {flat}}$ and ![]() $R_{\overline {\mathfrak {P}}}^{\leqslant \mu,\beta,\square }$ are flat
$R_{\overline {\mathfrak {P}}}^{\leqslant \mu,\beta,\square }$ are flat ![]() $\Lambda$-algebras (by construction and by Lemma 3.3.4) and
$\Lambda$-algebras (by construction and by Lemma 3.3.4) and ![]() $R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\beta,\square,\operatorname {flat}}[1/p]$ is reduced (which follows from Fact 2.4.2). Let
$R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\beta,\square,\operatorname {flat}}[1/p]$ is reduced (which follows from Fact 2.4.2). Let ![]() $A$ be the a finite flat
$A$ be the a finite flat ![]() $\Lambda$-algebra. An
$\Lambda$-algebra. An ![]() $A$-point of
$A$-point of ![]() $R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\beta,\square }$ is a
$R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\beta,\square }$ is a ![]() $G$-Kisin module
$G$-Kisin module ![]() $\mathfrak {P}$ with coefficients in
$\mathfrak {P}$ with coefficients in ![]() $A$ together with a Galois representation
$A$ together with a Galois representation ![]() $\rho : \Gamma _K \to G(A)$ extending
$\rho : \Gamma _K \to G(A)$ extending ![]() $\widetilde {T}_{G,A}(\mathfrak {P})$ (plus trivialization). After inverting
$\widetilde {T}_{G,A}(\mathfrak {P})$ (plus trivialization). After inverting ![]() $p$, we know that
$p$, we know that ![]() $\rho$ is crystalline with
$\rho$ is crystalline with ![]() $p$-adic Hodge type
$p$-adic Hodge type ![]() $\mu$ (see the discussion after Fact 2.4.2). Corollary 4.1.11 implies
$\mu$ (see the discussion after Fact 2.4.2). Corollary 4.1.11 implies ![]() $\mathfrak {P}[1/p]$ satisfies the monodromy condition. This gives the factorization. As
$\mathfrak {P}[1/p]$ satisfies the monodromy condition. This gives the factorization. As ![]() $R_{\overline {\mathfrak {P}}}^{\leqslant \mu,\beta,\square }$ surjects onto
$R_{\overline {\mathfrak {P}}}^{\leqslant \mu,\beta,\square }$ surjects onto ![]() $R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\beta,\square,\operatorname {flat}}$, we immediately see that
$R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\beta,\square,\operatorname {flat}}$, we immediately see that ![]() $R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta,\square,\nabla }$ surjects onto
$R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta,\square,\nabla }$ surjects onto ![]() $R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\beta,\square,\operatorname {flat}}$ and, hence, that
$R_{{\overline {\rho }},\overline {\mathfrak {P}}}^{\mu,\beta,\square,\operatorname {flat}}$ and, hence, that ![]() $\imath$ is a closed immersion.
$\imath$ is a closed immersion.
The remaining maps were discussed before the statement of the theorem. The square is cartesian by construction.
Using this, we can prove a technical version of our main theorem. Recall that ![]() $P_{\mu,\mathbf {F}}$ (respectively,
$P_{\mu,\mathbf {F}}$ (respectively, ![]() $P_{\mu ',\bf }$) are the parabolics over
$P_{\mu ',\bf }$) are the parabolics over ![]() $\mathbf {F}$ associated to the cocharacter
$\mathbf {F}$ associated to the cocharacter ![]() $\mu$ (respectively,
$\mu$ (respectively, ![]() $\mu '$).
$\mu '$).
Theorem 6.4.4 Suppose that ![]() $p \nmid \# \pi _1(G^{\mathrm {ad}})$. Fix a Galois representation
$p \nmid \# \pi _1(G^{\mathrm {ad}})$. Fix a Galois representation ![]() ${\overline {\rho }} : \Gamma _K \to G(\mathbf {F})$ with shape
${\overline {\rho }} : \Gamma _K \to G(\mathbf {F})$ with shape ![]() $\mu '$ and a Fontaine–Laffaille type
$\mu '$ and a Fontaine–Laffaille type ![]() $\mu$ for
$\mu$ for ![]() $G$ with
$G$ with ![]() $\mu$ and
$\mu$ and ![]() $\mu '$ dominant and
$\mu '$ dominant and ![]() $\mu ' \leqslant \mu$. Suppose that:
$\mu ' \leqslant \mu$. Suppose that:
(i)
 $\dim P_{\mu,\mathbf {F}} \backslash G_{\mathbf {F}} \geqslant \dim P_{\mu ', \mathbf {F}} \backslash G_{\mathbf {F}}$;
$\dim P_{\mu,\mathbf {F}} \backslash G_{\mathbf {F}} \geqslant \dim P_{\mu ', \mathbf {F}} \backslash G_{\mathbf {F}}$;(ii) the Kisin variety
 $Y^{\leqslant \mu }_{M_{G,\mathbf {F}}({\overline {\rho }})}$ is trivial; and
$Y^{\leqslant \mu }_{M_{G,\mathbf {F}}({\overline {\rho }})}$ is trivial; and(iii)
 $\operatorname {Spf} R_{{\overline {\rho }}}^{\mu,\square }$ is non-empty.
$\operatorname {Spf} R_{{\overline {\rho }}}^{\mu,\square }$ is non-empty.
Then ![]() $\operatorname {Spf} R_{{\overline {\rho }}}^{\mu,\square }$ is formally smooth.
$\operatorname {Spf} R_{{\overline {\rho }}}^{\mu,\square }$ is formally smooth.
Proof. We show that ![]() $\operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta,\square,\nabla }$ is either empty or formally smooth of the same dimension as
$\operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta,\square,\nabla }$ is either empty or formally smooth of the same dimension as ![]() $\operatorname {Spf} R^{\mu, \beta,\square,\operatorname {flat}}_{{\overline {\rho }},\overline {\mathfrak {P}}}$. Since
$\operatorname {Spf} R^{\mu, \beta,\square,\operatorname {flat}}_{{\overline {\rho }},\overline {\mathfrak {P}}}$. Since ![]() $\imath$ is a closed immersion, it follows that
$\imath$ is a closed immersion, it follows that ![]() $\operatorname {Spf} R^{\mu, \beta,\square,\operatorname {flat}}_{{\overline {\rho }},\overline {\mathfrak {P}}}$ and, hence,
$\operatorname {Spf} R^{\mu, \beta,\square,\operatorname {flat}}_{{\overline {\rho }},\overline {\mathfrak {P}}}$ and, hence, ![]() $\operatorname {Spf} R^{\mu,\square }_{{\overline {\rho }}}$ is formally smooth.
$\operatorname {Spf} R^{\mu,\square }_{{\overline {\rho }}}$ is formally smooth.
Let ![]() $\overline {C} \in \operatorname {LG}(\mathbf {F})$ correspond to
$\overline {C} \in \operatorname {LG}(\mathbf {F})$ correspond to ![]() $\varphi _{\overline {\mathfrak {P}}}$; it has shape
$\varphi _{\overline {\mathfrak {P}}}$; it has shape ![]() $\mu '$. Imposing the monodromy condition on the map from Proposition 3.3.7, we obtain a Cartesian diagram
$\mu '$. Imposing the monodromy condition on the map from Proposition 3.3.7, we obtain a Cartesian diagram

Note that ![]() $\operatorname {Spf} (R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta, \nabla })_\mathbf {F} \subset \operatorname {Spf} (R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta })_{\mathbf {F}}^ {\nabla }$ by Theorem 4.2.6. As
$\operatorname {Spf} (R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta, \nabla })_\mathbf {F} \subset \operatorname {Spf} (R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta })_{\mathbf {F}}^ {\nabla }$ by Theorem 4.2.6. As ![]() $\operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta, \nabla }$ involves imposing the monodromy condition and then taking the flat closure, it is conceivable that it is empty. The relative dimension of the bottom map is
$\operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta, \nabla }$ involves imposing the monodromy condition and then taking the flat closure, it is conceivable that it is empty. The relative dimension of the bottom map is ![]() $\dim G'_{(N)}$, where
$\dim G'_{(N)}$, where ![]() $N$ is the fixed integer from § 3.3 we have been using to define the deformation rings by trivializing
$N$ is the fixed integer from § 3.3 we have been using to define the deformation rings by trivializing ![]() $G$-Kisin modules modulo
$G$-Kisin modules modulo ![]() $E(u)^N$. The upper right formal scheme is formally smooth of dimension
$E(u)^N$. The upper right formal scheme is formally smooth of dimension ![]() $\dim P_{\mu ',\mathbf {F}} \backslash G_\mathbf {F}$ by Theorem 5.2.1. Thus
$\dim P_{\mu ',\mathbf {F}} \backslash G_\mathbf {F}$ by Theorem 5.2.1. Thus ![]() $\operatorname {Spf} (R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta, \nabla })_\mathbf {F}$ is either empty or formally smooth of dimension at most
$\operatorname {Spf} (R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta, \nabla })_\mathbf {F}$ is either empty or formally smooth of dimension at most ![]() $\dim P_{\mu ',\mathbf {F}} \backslash G'_\mathbf {F} + \dim G'_{(N)}$. Since, by definition,
$\dim P_{\mu ',\mathbf {F}} \backslash G'_\mathbf {F} + \dim G'_{(N)}$. Since, by definition, ![]() $R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta, \nabla }$ is
$R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta, \nabla }$ is ![]() $\Lambda$-flat, if
$\Lambda$-flat, if ![]() $\operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta, \nabla }$ is non-empty, then it is formally smooth of relative dimension at most
$\operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta, \nabla }$ is non-empty, then it is formally smooth of relative dimension at most ![]() $\dim P_{\mu ',\mathbf {F}} \backslash G'_\mathbf {F} + \dim G'_{(N)}$. We conclude that
$\dim P_{\mu ',\mathbf {F}} \backslash G'_\mathbf {F} + \dim G'_{(N)}$. We conclude that ![]() $\operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta,\square, \nabla }$ is either empty or formally smooth of relative dimension at most
$\operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta,\square, \nabla }$ is either empty or formally smooth of relative dimension at most
as the set of trivializations on the ![]() $\Gamma _\infty$-representation is a
$\Gamma _\infty$-representation is a ![]() $G_\mathbf {F}$-torsor. On the other hand, we assumed that
$G_\mathbf {F}$-torsor. On the other hand, we assumed that ![]() $\operatorname {Spf} R_{{\overline {\rho }}}^{\mu,\square }$ is non-empty. By Fact 2.4.2, we know it has relative dimension
$\operatorname {Spf} R_{{\overline {\rho }}}^{\mu,\square }$ is non-empty. By Fact 2.4.2, we know it has relative dimension ![]() $\dim G_{\mathbf {F}} + \dim P_{\mu, \mathbf {F}} \backslash G'_{\mathbf {F}}$. Hence,
$\dim G_{\mathbf {F}} + \dim P_{\mu, \mathbf {F}} \backslash G'_{\mathbf {F}}$. Hence, ![]() $\operatorname {Spf} R^{\mu, \beta,\square,\operatorname {flat}}_{{\overline {\rho }},\overline {\mathfrak {P}}}$ has relative dimension
$\operatorname {Spf} R^{\mu, \beta,\square,\operatorname {flat}}_{{\overline {\rho }},\overline {\mathfrak {P}}}$ has relative dimension
As ![]() $\dim P_{\mu,\mathbf {F}} \backslash G_{\mathbf {F}} \geqslant \dim P_{\mu ', \mathbf {F}} \backslash G_{\mathbf {F}}$, the existence of the closed immersion
$\dim P_{\mu,\mathbf {F}} \backslash G_{\mathbf {F}} \geqslant \dim P_{\mu ', \mathbf {F}} \backslash G_{\mathbf {F}}$, the existence of the closed immersion ![]() $\imath$ completes the proof.
$\imath$ completes the proof.
Remark 6.4.5
(i) When
 $\mu$ is a regular cocharacter, condition (i) is automatic.
$\mu$ is a regular cocharacter, condition (i) is automatic.(ii) We expect that
 $R_{{\overline {\rho }}}^{\mu,\square }$ is in fact zero when
$R_{{\overline {\rho }}}^{\mu,\square }$ is in fact zero when  $\mu ' \neq \mu$ so that condition (i) in Theorem 6.4.4 should not be necessary.
$\mu ' \neq \mu$ so that condition (i) in Theorem 6.4.4 should not be necessary.
Theorem A is a direct consequence.
Proof of Theorem A Take ![]() $\mu ' = \mu$ to guarantee condition (i) in Theorem 6.4.4, and use Corollary 6.1.12 to guarantee condition (ii).
$\mu ' = \mu$ to guarantee condition (i) in Theorem 6.4.4, and use Corollary 6.1.12 to guarantee condition (ii).
Finally, note that ![]() $\operatorname {Spf} R_{{\overline {\rho }}}^{\mu,\square }$ is non-empty if and only if there exists a crystalline lift of
$\operatorname {Spf} R_{{\overline {\rho }}}^{\mu,\square }$ is non-empty if and only if there exists a crystalline lift of ![]() ${\overline {\rho }}$ with
${\overline {\rho }}$ with ![]() $p$-adic Hodge type
$p$-adic Hodge type ![]() $\mu$. We now record a few partial results about the non-existence of crystalline lifts which follow from our methods.
$\mu$. We now record a few partial results about the non-existence of crystalline lifts which follow from our methods.
Corollary 6.4.6 With the setup of Theorem 6.4.4, assume that condition (ii) holds but that ![]() $\dim P_{\mu,\mathbf {F}} \backslash G_{\mathbf {F}} < \dim P_{\mu ',\mathbf {F}} \backslash G_{\mathbf {F}}$. Then there does not exist a crystalline lift of
$\dim P_{\mu,\mathbf {F}} \backslash G_{\mathbf {F}} < \dim P_{\mu ',\mathbf {F}} \backslash G_{\mathbf {F}}$. Then there does not exist a crystalline lift of ![]() ${\overline {\rho }}$ with
${\overline {\rho }}$ with ![]() $p$-adic Hodge type
$p$-adic Hodge type ![]() $\mu$.
$\mu$.
Proof. By hypothesis (6.4.2) is larger than (6.4.3). Then the proof of Theorem 6.4.4 shows that ![]() $\operatorname {Spf} R^{\mu, \beta,\square,\operatorname {flat}}_{{\overline {\rho }},\overline {\mathfrak {P}}}$ is either empty or has relative dimension larger than the relative dimension of
$\operatorname {Spf} R^{\mu, \beta,\square,\operatorname {flat}}_{{\overline {\rho }},\overline {\mathfrak {P}}}$ is either empty or has relative dimension larger than the relative dimension of ![]() $\operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta,\square, \nabla }$. As there is a closed immersion
$\operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta,\square, \nabla }$. As there is a closed immersion ![]() $\imath : \operatorname {Spf} R^{\mu, \beta,\square,\operatorname {flat}}_{{\overline {\rho }},\overline {\mathfrak {P}}} \to \operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta,\square, \nabla }$, we conclude that
$\imath : \operatorname {Spf} R^{\mu, \beta,\square,\operatorname {flat}}_{{\overline {\rho }},\overline {\mathfrak {P}}} \to \operatorname {Spf} R_{\overline {\mathfrak {P}}}^{\leqslant \mu, \beta,\square, \nabla }$, we conclude that ![]() $\operatorname {Spf} R^{\mu, \beta,\square,\operatorname {flat}}_{{\overline {\rho }},\overline {\mathfrak {P}}}$ is empty.
$\operatorname {Spf} R^{\mu, \beta,\square,\operatorname {flat}}_{{\overline {\rho }},\overline {\mathfrak {P}}}$ is empty.
Remark 6.4.7 The techniques of this paper can also be adapted to show that the existence of a crystalline lift of type ![]() $\mu$ satisfying the hypotheses (i) and (ii) from Theorem A implies non-existence of a crystalline lift of weight
$\mu$ satisfying the hypotheses (i) and (ii) from Theorem A implies non-existence of a crystalline lift of weight ![]() $\mu '$ for
$\mu '$ for ![]() $\mu ' < \mu$. This is a motivation for the expectation in Remark 6.4.5(2).
$\mu ' < \mu$. This is a motivation for the expectation in Remark 6.4.5(2).
Acknowledgements
We thank Matthew Emerton, Toby Gee, Florian Herzig, Timo Richarz, and Niccolo’ Ronchetti for helpful conversations. We thank the referees for a very careful reading. The first author was partially supported by the Marsden Fund Council administered by the Royal Society of New Zealand. The second author was supported by a grant from the Simons Foundation/SFARI (#585753) and supported in part by NSF Grant DMS-1952556.
Conflicts of Interest
None.