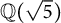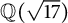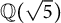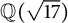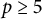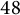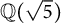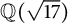1 Introduction
The celebrated Fermat’s Last Theorem was proven in [Reference Taylor and Wiles19, Reference Wiles22] by Taylor-Wiles and Wiles. Ever since then, it has been natural to attempt to use the same methods to tackle more general forms of the Fermat equation, particularly the still unresolved Beal conjecture [Reference Mauldin16].
Another direction has been to study the usual Fermat equation over number fields. For instance, Freitas and Siksek considered, in [Reference Freitas and Siksek10, Reference Freitas and Siksek11], Fermat’s Last Theorem over real quadratic fields. In particular, it is currently known that Fermat’s Last Theorem is asymptotically true for
![]() $K = \mathbb {Q}(\sqrt {d})$
where
$K = \mathbb {Q}(\sqrt {d})$
where
![]() $2 \le d \le 23$
square-free and
$2 \le d \le 23$
square-free and
![]() $d \not = 5, 17$
and also on a subset of d which has density
$d \not = 5, 17$
and also on a subset of d which has density
![]() $5/6$
among square-free
$5/6$
among square-free
![]() $d> 0$
. For a given number field K, asymptotically true means that Fermat’s Last Theorem is true for sufficiently large exponents. In a different vein, [Reference Freitas, Kraus and Siksek6–Reference Freitas, Kraus and Siksek8] establish more general criteria for proving the asymptotic Fermat’s Last Theorem and apply these to a number of infinite families of number fields.
$d> 0$
. For a given number field K, asymptotically true means that Fermat’s Last Theorem is true for sufficiently large exponents. In a different vein, [Reference Freitas, Kraus and Siksek6–Reference Freitas, Kraus and Siksek8] establish more general criteria for proving the asymptotic Fermat’s Last Theorem and apply these to a number of infinite families of number fields.
In this paper, we study Fermat’s Last Theorem over K for
![]() $d = 5$
and
$d = 5$
and
![]() $d = 17$
, the first two notable cases where asymptotic results are not yet proved. These cases present difficulties within the framework of [Reference Freitas and Siksek11] due to a large number of solutions to the S-unit equation over K where S is the set of primes of K above
$d = 17$
, the first two notable cases where asymptotic results are not yet proved. These cases present difficulties within the framework of [Reference Freitas and Siksek11] due to a large number of solutions to the S-unit equation over K where S is the set of primes of K above
![]() $2$
. We circumvent these obstructions by showing that the reciprocity constraints in [Reference Bennett, Chen, Dahmen and Yazdani1, Reference Chen and Siksek4] generalize to a real quadratic base field, allowing a complete resolution in certain congruence classes of prime exponents p. In addition to [Reference Bennett, Chen, Dahmen and Yazdani1, Reference Chen and Siksek4], we also mention [Reference Deconinck5, Reference Ibrahim14] where reciprocity constraints have been used to solve generalized Fermat equations.
$2$
. We circumvent these obstructions by showing that the reciprocity constraints in [Reference Bennett, Chen, Dahmen and Yazdani1, Reference Chen and Siksek4] generalize to a real quadratic base field, allowing a complete resolution in certain congruence classes of prime exponents p. In addition to [Reference Bennett, Chen, Dahmen and Yazdani1, Reference Chen and Siksek4], we also mention [Reference Deconinck5, Reference Ibrahim14] where reciprocity constraints have been used to solve generalized Fermat equations.
Let K be a quadratic field, and let
![]() $\mathcal {O}_K$
be its ring of integers. Assume that K has class number one. We say that a solution
$\mathcal {O}_K$
be its ring of integers. Assume that K has class number one. We say that a solution
![]() $(a,b,c)$
over
$(a,b,c)$
over
![]() $\mathcal {O}_K$
, i.e., where
$\mathcal {O}_K$
, i.e., where
![]() $a,b,c \in \mathcal {O}_K$
, to
$a,b,c \in \mathcal {O}_K$
, to
is primitive if the ideal
![]() $(a,b,c) = \mathcal {O}_K$
and nontrivial if
$(a,b,c) = \mathcal {O}_K$
and nontrivial if
![]() $abc \not = 0$
.
$abc \not = 0$
.
Under the assumption that K has class number one, we note that any nonzero solution
![]() $(a,b,c) \in K^3$
to (1.1) can be scaled to a primitive solution over
$(a,b,c) \in K^3$
to (1.1) can be scaled to a primitive solution over
![]() $\mathcal {O}_K$
, and henceforth, when we refer to solutions over K, we mean that the solutions have been scaled to a primitive solution over
$\mathcal {O}_K$
, and henceforth, when we refer to solutions over K, we mean that the solutions have been scaled to a primitive solution over
![]() $\mathcal {O}_K$
. In the more general case that K does not have class number one, we refer the reader to [Reference Freitas and Siksek11].
$\mathcal {O}_K$
. In the more general case that K does not have class number one, we refer the reader to [Reference Freitas and Siksek11].
Theorem 1.2 There are no nontrivial primitive solutions over
![]() $\mathbb {Q}(\sqrt {5})$
to
$\mathbb {Q}(\sqrt {5})$
to
for prime
![]() $p \ge 5$
if p satisfies one of the following:
$p \ge 5$
if p satisfies one of the following:
-
(1)
 $p \equiv 5,7 \ \pmod 8$
, or
$p \equiv 5,7 \ \pmod 8$
, or -
(2)
 $p \equiv 19, 41 \ \pmod {48}$
.
$p \equiv 19, 41 \ \pmod {48}$
.
The above theorem shows that Fermat’s Last Theorem over
![]() $\mathbb {Q}(\sqrt {5})$
is true for a set of prime exponents with Dirichlet density
$\mathbb {Q}(\sqrt {5})$
is true for a set of prime exponents with Dirichlet density
![]() $5/8$
. In [Reference Kraus15], Theorem 1.2 is proved for
$5/8$
. In [Reference Kraus15], Theorem 1.2 is proved for
![]() $5 \le p < 10^7$
, where we note that the small exponents in this range rely on [Reference Hao and Parry13]. The method used in [Reference Kraus15] is to fix a prime exponent
$5 \le p < 10^7$
, where we note that the small exponents in this range rely on [Reference Hao and Parry13]. The method used in [Reference Kraus15] is to fix a prime exponent
![]() $p \ge 11$
and use an auxiliary prime
$p \ge 11$
and use an auxiliary prime
![]() $q = pk+1$
with
$q = pk+1$
with
![]() $k < p-2$
and q split in K, and apply the modular method together with the local condition mod q on solutions to (1.1). In practice, it appears that most primes q of this form succeed in giving a proof for the fixed exponent p, but there is no currently known way to prove results of this type in general.
$k < p-2$
and q split in K, and apply the modular method together with the local condition mod q on solutions to (1.1). In practice, it appears that most primes q of this form succeed in giving a proof for the fixed exponent p, but there is no currently known way to prove results of this type in general.
Theorem 1.3 There are no nontrivial primitive solutions over
![]() $\mathbb {Q}(\sqrt {17})$
to
$\mathbb {Q}(\sqrt {17})$
to
for prime
![]() $p \ge 5$
if p satisfies one of the following:
$p \ge 5$
if p satisfies one of the following:
-
(1)
 $p \equiv 5, 7 \ \pmod 8$
, or
$p \equiv 5, 7 \ \pmod 8$
, or -
(2)
 $p \equiv 17 \ \pmod {24}$
.
$p \equiv 17 \ \pmod {24}$
.
Remark 1.4 In [Reference Freitas and Siksek11], Theorem 1.3 is established for
![]() $p \equiv 3, 5 \ \pmod 8$
using the symplectic method [Reference Halberstadt and Kraus12]. The above theorem and the result in [Reference Freitas and Siksek11] imply the corollary below, which shows that Fermat’s Last Theorem over
$p \equiv 3, 5 \ \pmod 8$
using the symplectic method [Reference Halberstadt and Kraus12]. The above theorem and the result in [Reference Freitas and Siksek11] imply the corollary below, which shows that Fermat’s Last Theorem over
![]() $K = \mathbb {Q}(\sqrt {17})$
is true for a set of prime exponents with Dirichlet density
$K = \mathbb {Q}(\sqrt {17})$
is true for a set of prime exponents with Dirichlet density
![]() $7/8$
.
$7/8$
.
Corollary 1.5 There are no nontrivial primitive solutions over
![]() $\mathbb {Q}(\sqrt {17})$
to
$\mathbb {Q}(\sqrt {17})$
to
for prime
![]() $p \ge 5$
if
$p \ge 5$
if
![]() $p \not \equiv 1 \ \pmod {24}$
.
$p \not \equiv 1 \ \pmod {24}$
.
The proofs of the above theorems are based on the modular method, which attaches a Frey elliptic curve
![]() $E_0$
defined over K to a putative nontrivial primitive solution. One then considers the representation
$E_0$
defined over K to a putative nontrivial primitive solution. One then considers the representation
![]() ${\overline {\rho }}_{E_0,p} : G_K \rightarrow \operatorname {GL}_2(\mathbb {F}_p)$
on the p-torsion points of
${\overline {\rho }}_{E_0,p} : G_K \rightarrow \operatorname {GL}_2(\mathbb {F}_p)$
on the p-torsion points of
![]() $E_0$
, which, by virtue of being a Frey elliptic curve, has Artin conductor bounded independently of the solution and prime exponent p.
$E_0$
, which, by virtue of being a Frey elliptic curve, has Artin conductor bounded independently of the solution and prime exponent p.
Using modularity and level lowering, one deduces that
![]() ${\overline {\rho }}_{E_0,p} \cong {\overline {\rho }}_{f,p}$
, where
${\overline {\rho }}_{E_0,p} \cong {\overline {\rho }}_{f,p}$
, where
![]() ${\overline {\rho }}_{f,p} : G_K \rightarrow \operatorname {GL}_2(\mathbb {F}_p)$
is the residual Galois representation attached to a Hilbert newform at the possible Artin conductors. For the cases considered in this paper, f has a coefficient field equal to the field of rational numbers.
${\overline {\rho }}_{f,p} : G_K \rightarrow \operatorname {GL}_2(\mathbb {F}_p)$
is the residual Galois representation attached to a Hilbert newform at the possible Artin conductors. For the cases considered in this paper, f has a coefficient field equal to the field of rational numbers.
Unlike the original Fermat’s Last Theorem, the space of newforms with level equal to the possible Artin conductor is typically not zero. Hence, to achieve a contradiction, one needs additional methods. To accomplish this, we combine information from reciprocity constraints such as in [Reference Chen and Siksek4] to obtain a contradiction for prime exponents in certain congruence classes. This succeeds for
![]() $\mathbb {Q}(\sqrt {5})$
; however, the reciprocity constraint used in [Reference Chen and Siksek4] is not strong enough to treat
$\mathbb {Q}(\sqrt {5})$
; however, the reciprocity constraint used in [Reference Chen and Siksek4] is not strong enough to treat
![]() $\mathbb {Q}(\sqrt {17})$
.
$\mathbb {Q}(\sqrt {17})$
.
Using the approach in [Reference Bennett, Chen, Dahmen and Yazdani1], valid over
![]() $\mathbb {Q}$
, we prove a stronger reciprocity constraint, valid over certain real quadratic base fields, in terms of Hilbert symbols. This has an added advantage that the reciprocity law needed is simply the well-known reciprocity law for Hilbert symbols over a number field [Reference Voight21].
$\mathbb {Q}$
, we prove a stronger reciprocity constraint, valid over certain real quadratic base fields, in terms of Hilbert symbols. This has an added advantage that the reciprocity law needed is simply the well-known reciprocity law for Hilbert symbols over a number field [Reference Voight21].
The programs and output transcripts for the computations needed in this paper are described and posted at [Reference Chen, Efemwonkieke and Sun3].
2 Proof of Theorem 1.2
Let
![]() $K = \mathbb {Q}(\sqrt {5})$
and note that
$K = \mathbb {Q}(\sqrt {5})$
and note that
![]() $\mathcal {O}_K$
has unique factorization. Suppose
$\mathcal {O}_K$
has unique factorization. Suppose
![]() $(a,b,c)$
is a nontrivial primitive solution over
$(a,b,c)$
is a nontrivial primitive solution over
![]() $\mathcal {O}_K$
to (1.1) for a prime
$\mathcal {O}_K$
to (1.1) for a prime
![]() $p \ge 5$
. Normalize the solution
$p \ge 5$
. Normalize the solution
![]() $(a,b,c)$
as in [Reference Kraus15].
$(a,b,c)$
as in [Reference Kraus15].
Let
![]() $E_0$
denote the Frey elliptic curve over K:
$E_0$
denote the Frey elliptic curve over K:
Let
![]() $\mathfrak {P}$
be the unique prime of K above
$\mathfrak {P}$
be the unique prime of K above
![]() $2$
.
$2$
.
Proposition 2.2 Assuming
![]() $p \ge 5$
, the conductor of
$p \ge 5$
, the conductor of
![]() $E_0$
over K is given by
$E_0$
over K is given by
where
![]() $t \in \{1,2,3\}$
. Moreover,
$t \in \{1,2,3\}$
. Moreover,
![]() $t = 1$
if
$t = 1$
if
![]() $2 \mid abc$
and
$2 \mid abc$
and
![]() $t \in \left \{ 2, 3 \right \}$
if
$t \in \left \{ 2, 3 \right \}$
if
![]() $2 \nmid abc$
.
$2 \nmid abc$
.
Proof See [Reference Kraus15, Lemme 3].
Proposition 2.3 The representation
![]() ${\overline {\rho }}_{E_0,p} : G_K \rightarrow \operatorname {GL}_2(\mathbb {F}_p)$
is irreducible if
${\overline {\rho }}_{E_0,p} : G_K \rightarrow \operatorname {GL}_2(\mathbb {F}_p)$
is irreducible if
![]() $p \ge 11$
.
$p \ge 11$
.
Proof See [Reference Kraus15, Proposition, p. 7].
Proposition 2.4 There is a Hilbert newform f of trivial character, parallel weight
![]() $2$
, and level
$2$
, and level
![]() $\mathfrak {P}^t$
such that
$\mathfrak {P}^t$
such that
![]() ${\overline {\rho }}_{E_0,p} \simeq {\overline {\rho }}_{f,\mathfrak {p}}$
.
${\overline {\rho }}_{E_0,p} \simeq {\overline {\rho }}_{f,\mathfrak {p}}$
.
Proof The elliptic curve
![]() $E_0$
over K is modular by [Reference Freitas, LeHung and Siksek9]. Using [Reference Freitas and Siksek10, Theorem 7], we obtain the desired statement.
$E_0$
over K is modular by [Reference Freitas, LeHung and Siksek9]. Using [Reference Freitas and Siksek10, Theorem 7], we obtain the desired statement.
The space of Hilbert newforms of trivial character, parallel weight
![]() $2$
, and level
$2$
, and level
![]() $\mathfrak {P}, \mathfrak {P}^2$
is zero, so these cases do not occur. In particular, we may now assume that
$\mathfrak {P}, \mathfrak {P}^2$
is zero, so these cases do not occur. In particular, we may now assume that
and
![]() $t = 3$
.
$t = 3$
.
There is a unique Hilbert newform f of trivial character, parallel weight
![]() $2$
, and level
$2$
, and level
![]() $\mathfrak {P}^3$
which corresponds to an elliptic curve E over K. Hence, we have that
$\mathfrak {P}^3$
which corresponds to an elliptic curve E over K. Hence, we have that
by Proposition 2.4.
Lemma 2.7 The elliptic curve E over K is given by
Proof The conductor of E over K is
![]() $\mathfrak {P}^3$
. Since E is modular, it corresponds to the unique Hilbert newform f of trivial character, parallel weight
$\mathfrak {P}^3$
. Since E is modular, it corresponds to the unique Hilbert newform f of trivial character, parallel weight
![]() $2$
, and level
$2$
, and level
![]() $\mathfrak {P}^3$
.
$\mathfrak {P}^3$
.
Remark 2.8 In the last section, we explain how to determine the full list of solutions
![]() $(a,b,c)$
to
$(a,b,c)$
to
![]() $a + b + c = 0$
, up to multiplication by the square of a unit of
$a + b + c = 0$
, up to multiplication by the square of a unit of
![]() $\mathcal {O}_K$
, such that
$\mathcal {O}_K$
, such that
gives rise to an elliptic curve in the same isogeny class of E over K. We remark that the
![]() $2$
-adic conditions on these
$2$
-adic conditions on these
![]() $(a,b,c)$
vary; in particular, there are some triples where
$(a,b,c)$
vary; in particular, there are some triples where
![]() $2 \nmid abc$
. This implies that inertia arguments at
$2 \nmid abc$
. This implies that inertia arguments at
![]() $2$
will fail as any solution which is
$2$
will fail as any solution which is
![]() $2$
-adically close to one of these triples
$2$
-adically close to one of these triples
![]() $(a,b,c)$
cannot be ruled out by inertia arguments at
$(a,b,c)$
cannot be ruled out by inertia arguments at
![]() $2$
.
$2$
.
Let
![]() $L = K(\zeta _r)$
where
$L = K(\zeta _r)$
where
![]() $\zeta _r$
is a primitive rth root of unity. Using modularity arguments and Theorem 3.5 in the following cases involving values of r, we will prove Theorem 1.2.
$\zeta _r$
is a primitive rth root of unity. Using modularity arguments and Theorem 3.5 in the following cases involving values of r, we will prove Theorem 1.2.
-
(1) Case
 $r=1$
.
$r=1$
.Let
 $k = \mathcal {O}_K/3 \mathcal {O}_K \cong \mathbb {F}_9$
, noting that
$k = \mathcal {O}_K/3 \mathcal {O}_K \cong \mathbb {F}_9$
, noting that
 $\# k^\times = 8$
.
$\# k^\times = 8$
.Let
 $\mathfrak {q}_3 = 3 \mathcal {O}_K$
and
$\mathfrak {q}_3 = 3 \mathcal {O}_K$
and
 $N(\mathfrak {q}_3) = 9$
be the norm of
$N(\mathfrak {q}_3) = 9$
be the norm of
 $\mathfrak {q}_3$
.
$\mathfrak {q}_3$
.If
 $abc = 0$
in k, then we obtain a bound on p by [Reference Kraus15, p. 9]. In particular, if
$abc = 0$
in k, then we obtain a bound on p by [Reference Kraus15, p. 9]. In particular, if
 $p \not = 3$
, then p divides (2.9)which is nonzero by the Hasse bound
$p \not = 3$
, then p divides (2.9)which is nonzero by the Hasse bound $$ \begin{align} a_{\mathfrak{q}_3}(f) \pm (N(\mathfrak{q}_3) +1) \not= 0, \end{align} $$
(2.10)
$$ \begin{align} a_{\mathfrak{q}_3}(f) \pm (N(\mathfrak{q}_3) +1) \not= 0, \end{align} $$
(2.10) $$ \begin{align} | a_{\mathfrak{q}_3}(f)| = |a_{\mathfrak{q}_3}(E)| \le 2 \sqrt{N(\mathfrak{q}_3)}. \end{align} $$
$$ \begin{align} | a_{\mathfrak{q}_3}(f)| = |a_{\mathfrak{q}_3}(E)| \le 2 \sqrt{N(\mathfrak{q}_3)}. \end{align} $$
If
 $a_{\mathfrak {q}_3}(E_0) \not = a_{\mathfrak {q}_3}(E)$
, then we also obtain a bound on p by [Reference Kraus15, p. 9]. In particular, if
$a_{\mathfrak {q}_3}(E_0) \not = a_{\mathfrak {q}_3}(E)$
, then we also obtain a bound on p by [Reference Kraus15, p. 9]. In particular, if
 $p \not = 3$
, then p divides (2.11)
$p \not = 3$
, then p divides (2.11) $$ \begin{align} a_{\mathfrak{q}_3}(E_0) - a_{\mathfrak{q}_3}(E) \not= 0. \end{align} $$
$$ \begin{align} a_{\mathfrak{q}_3}(E_0) - a_{\mathfrak{q}_3}(E) \not= 0. \end{align} $$
Thus, either we obtain a bound on p or we have that
 $a,b,c \in k^\times $
and
$a,b,c \in k^\times $
and
 $a_{\mathfrak {q}_3}(E_0) = a_{\mathfrak {q}_3}(E)$
. The bound can be computed to be
$a_{\mathfrak {q}_3}(E_0) = a_{\mathfrak {q}_3}(E)$
. The bound can be computed to be
 $p \in \left \{ 2,3 \right \}$
.
$p \in \left \{ 2,3 \right \}$
.Assume now that
 $a,b,c \in k^\times $
and
$a,b,c \in k^\times $
and
 $a_{\mathfrak {q}_3}(E_0) = a_{\mathfrak {q}_3}(E)$
. Now, set (2.12)
$a_{\mathfrak {q}_3}(E_0) = a_{\mathfrak {q}_3}(E)$
. Now, set (2.12) $$ \begin{align} \epsilon = a^p b^p c^{-2p} \text{ in } k. \end{align} $$
$$ \begin{align} \epsilon = a^p b^p c^{-2p} \text{ in } k. \end{align} $$
Since
 $p^2 \equiv 1 \ \pmod 8$
, we have that
$p^2 \equiv 1 \ \pmod 8$
, we have that
 $\epsilon ^R = ab c^{-2}$
in k where
$\epsilon ^R = ab c^{-2}$
in k where
 $R \equiv p \ \pmod 8$
. Hence, the condition (3.6) becomes (2.13)for all permutations of
$R \equiv p \ \pmod 8$
. Hence, the condition (3.6) becomes (2.13)for all permutations of $$ \begin{align} \left(\frac{\epsilon^R-1}{3}\right)_{K} \not= -1, \end{align} $$
$$ \begin{align} \left(\frac{\epsilon^R-1}{3}\right)_{K} \not= -1, \end{align} $$
 $a,b,c$
as (2.5) holds. Using
$a,b,c$
as (2.5) holds. Using
 $\mathsf{Magma}$
, we can check the set of triples
$\mathsf{Magma}$
, we can check the set of triples
 $(a,b,c) \in (k^\times )^3$
which satisfy and (2.13) for all permutations of
$(a,b,c) \in (k^\times )^3$
which satisfy and (2.13) for all permutations of $$ \begin{align*} a_{\mathfrak{q}_3}(E_0) = a_{\mathfrak{q}_3}(E), \end{align*} $$
$$ \begin{align*} a_{\mathfrak{q}_3}(E_0) = a_{\mathfrak{q}_3}(E), \end{align*} $$
 $a,b,c$
is empty if
$a,b,c$
is empty if
 $p \equiv 5, 7 \ \pmod {8}$
.
$p \equiv 5, 7 \ \pmod {8}$
.
-
(2) Case
 $r = 3$
.
$r = 3$
.Let
 $k = \mathcal {O}_K/21 \mathcal {O}_K \cong \mathbb {F}_9 \times \mathbb {F}_{49}$
, noting that
$k = \mathcal {O}_K/21 \mathcal {O}_K \cong \mathbb {F}_9 \times \mathbb {F}_{49}$
, noting that
 $\# k^\times = 384$
. Let
$\# k^\times = 384$
. Let
 $\mathfrak {q}_3 = 3 \mathcal {O}_K$
and
$\mathfrak {q}_3 = 3 \mathcal {O}_K$
and
 $\mathfrak {q}_7 = 7 \mathcal {O}_K$
.
$\mathfrak {q}_7 = 7 \mathcal {O}_K$
.If
 $abc \notin k^\times $
or one of the following two conditions holds, we obtain a bound on p similarly as in (2.9) and (2.11). This bound can be computed to be
$abc \notin k^\times $
or one of the following two conditions holds, we obtain a bound on p similarly as in (2.9) and (2.11). This bound can be computed to be $$ \begin{align*} a_{\mathfrak{q}_3}(E_0) & \not= a_{\mathfrak{q}_3}(E), \\ a_{\mathfrak{q}_7}(E_0) & \not= a_{\mathfrak{q}_7}(E), \end{align*} $$
$$ \begin{align*} a_{\mathfrak{q}_3}(E_0) & \not= a_{\mathfrak{q}_3}(E), \\ a_{\mathfrak{q}_7}(E_0) & \not= a_{\mathfrak{q}_7}(E), \end{align*} $$
 $p \in \left \{ 2,3,5 \right \}$
. The case
$p \in \left \{ 2,3,5 \right \}$
. The case
 $p = 5$
is covered by [Reference Kraus15].
$p = 5$
is covered by [Reference Kraus15].
Assume from here on that
 $a,b,c \in k^\times $
and both hold. Now set
$a,b,c \in k^\times $
and both hold. Now set $$ \begin{align*} a_{\mathfrak{q}_3}(E_0) & = a_{\mathfrak{q}_3}(E) \quad\text{and} \\ a_{\mathfrak{q}_7}(E_0) & = a_{\mathfrak{q}_7}(E) \end{align*} $$
(2.14)
$$ \begin{align*} a_{\mathfrak{q}_3}(E_0) & = a_{\mathfrak{q}_3}(E) \quad\text{and} \\ a_{\mathfrak{q}_7}(E_0) & = a_{\mathfrak{q}_7}(E) \end{align*} $$
(2.14) $$ \begin{align} \epsilon = a^p b^p c^{-2p} \text{ in } k. \end{align} $$
$$ \begin{align} \epsilon = a^p b^p c^{-2p} \text{ in } k. \end{align} $$
Let
 $R^{*}$
be the least positive residue such that
$R^{*}$
be the least positive residue such that
 $p \equiv R^* \ \pmod {384}$
, and let R be such that
$p \equiv R^* \ \pmod {384}$
, and let R be such that
 $R R^* \equiv 1 \ \pmod {384}$
. Then we have that
$R R^* \equiv 1 \ \pmod {384}$
. Then we have that
 $\epsilon ^R = ab c^{-2}$
in k. Hence, the condition (3.6), taking
$\epsilon ^R = ab c^{-2}$
in k. Hence, the condition (3.6), taking
 $\zeta _r' = \zeta _r^R$
since
$\zeta _r' = \zeta _r^R$
since
 $r = 3$
divides
$r = 3$
divides
 $384$
, becomes (2.15)for all permutations of
$384$
, becomes (2.15)for all permutations of $$ \begin{align} \left(\frac{\epsilon^R - \zeta_r'}{1- 4 \zeta_r}\right)_{K} \not= -1, \end{align} $$
$$ \begin{align} \left(\frac{\epsilon^R - \zeta_r'}{1- 4 \zeta_r}\right)_{K} \not= -1, \end{align} $$
 $a,b,c$
as (2.5) holds. Using
$a,b,c$
as (2.5) holds. Using
 $\mathsf{Magma}$
, we can check the set of triples
$\mathsf{Magma}$
, we can check the set of triples
 $(a,b,c) \in (k^\times )^3$
which satisfy and (2.15) for all permutations of
$(a,b,c) \in (k^\times )^3$
which satisfy and (2.15) for all permutations of $$ \begin{align*} a_{\mathfrak{q}_3}(E_0) & = a_{\mathfrak{q}_3}(E), \\ a_{\mathfrak{q}_7}(E_0) & = a_{\mathfrak{q}_7}(E), \end{align*} $$
$$ \begin{align*} a_{\mathfrak{q}_3}(E_0) & = a_{\mathfrak{q}_3}(E), \\ a_{\mathfrak{q}_7}(E_0) & = a_{\mathfrak{q}_7}(E), \end{align*} $$
 $a,b,c$
is empty if
$a,b,c$
is empty if  $$ \begin{align*} & p \equiv 7, 19, 29, 41, 55, 67, 77, 89, 103, 115, 125, 137, 151, 163, 173, 185, \\ & 199, 211, 221, 233, 247, 259, 269, 281, 295, 307, 317, 329, 343, 355, 365, 377 \ \pmod{384}. \end{align*} $$
$$ \begin{align*} & p \equiv 7, 19, 29, 41, 55, 67, 77, 89, 103, 115, 125, 137, 151, 163, 173, 185, \\ & 199, 211, 221, 233, 247, 259, 269, 281, 295, 307, 317, 329, 343, 355, 365, 377 \ \pmod{384}. \end{align*} $$
It can be verified that the set of congruence condition above is equivalent to
 $p \equiv 7, 19, 29, 41 \ \pmod {48}$
, noting that
$p \equiv 7, 19, 29, 41 \ \pmod {48}$
, noting that
 $48$
divides
$48$
divides
 $384$
.
$384$
.
This concludes the proof of Theorem 1.2.
Remark 2.16 In the proof of Theorem 1.2, we argued on a hypothetical solution
![]() $(a,b,c)$
to
$(a,b,c)$
to
![]() $a^p + b^p + c^p = 0$
and applied constraints over the residue class ring k. However, since p is coprime to
$a^p + b^p + c^p = 0$
and applied constraints over the residue class ring k. However, since p is coprime to
![]() $\# k^\times $
, we can check the modular and reciprocity constraints in terms of new variables
$\# k^\times $
, we can check the modular and reciprocity constraints in terms of new variables
![]() $(a',b',c') = (a^p,b^p,c^p)$
in
$(a',b',c') = (a^p,b^p,c^p)$
in
![]() $k^3$
. This remark also applies to Theorem 1.3.
$k^3$
. This remark also applies to Theorem 1.3.
Remark 2.17 For a given
![]() $r \ge 1$
, let
$r \ge 1$
, let
![]() $K = \mathbb {Q}(\sqrt {d})$
and
$K = \mathbb {Q}(\sqrt {d})$
and
![]() $L = \mathbb {Q}(\sqrt {d},\zeta _r)$
. Our method of obtaining results for the Fermat’s Last Theorem over K requires us to check the reciprocity constraints for all
$L = \mathbb {Q}(\sqrt {d},\zeta _r)$
. Our method of obtaining results for the Fermat’s Last Theorem over K requires us to check the reciprocity constraints for all
![]() $3$
-tuples
$3$
-tuples
![]() $(a,b,c) \in k_r^3$
where
$(a,b,c) \in k_r^3$
where
![]() $k_r$
is the residue ring given by
$k_r$
is the residue ring given by
and
![]() $\mathfrak {N}_r := (1-4\zeta _r)\mathcal {O}_L \cap \mathcal {O}_K$
. As we increase r, the size of the rational prime factors of
$\mathfrak {N}_r := (1-4\zeta _r)\mathcal {O}_L \cap \mathcal {O}_K$
. As we increase r, the size of the rational prime factors of
![]() $\text {Norm}(1 - 4\zeta _r)$
grows rapidly, which leads to computational bottlenecks as then
$\text {Norm}(1 - 4\zeta _r)$
grows rapidly, which leads to computational bottlenecks as then
![]() $k_r$
is too large (implying that the number of
$k_r$
is too large (implying that the number of
![]() $R^*$
and triples
$R^*$
and triples
![]() $(a,b,c) \in k_r^3$
to consider are too numerous or the Hecke eigenvalue computation for the modular constraint is infeasible). We therefore restricted our search for results to
$(a,b,c) \in k_r^3$
to consider are too numerous or the Hecke eigenvalue computation for the modular constraint is infeasible). We therefore restricted our search for results to
![]() $r \le 10$
.
$r \le 10$
.
Remark 2.18 We describe more specifically how Remark 2.17 applies to
![]() $d = 5$
: if
$d = 5$
: if
![]() $r = 2$
, then
$r = 2$
, then
![]() $(1-4\zeta _2)\mathcal {O}_L = (\sqrt {5} \mathcal {O}_L)^2$
so that
$(1-4\zeta _2)\mathcal {O}_L = (\sqrt {5} \mathcal {O}_L)^2$
so that
 $$ \begin{align} {\left(\frac{{ab-c^2\zeta_r'}}{5}\right)_{L}} = \left(\frac{ab-c^2\zeta_r'}{\sqrt{5}}\right)_{L}\left(\frac{ab-c^2\zeta_r'}{\sqrt{5}}\right)_{L} = 1 \ne -1 \end{align} $$
$$ \begin{align} {\left(\frac{{ab-c^2\zeta_r'}}{5}\right)_{L}} = \left(\frac{ab-c^2\zeta_r'}{\sqrt{5}}\right)_{L}\left(\frac{ab-c^2\zeta_r'}{\sqrt{5}}\right)_{L} = 1 \ne -1 \end{align} $$
for any
![]() $(a,b,c) \in k_r^3$
; that is, we obtain a trivial reciprocity constraint. For
$(a,b,c) \in k_r^3$
; that is, we obtain a trivial reciprocity constraint. For
![]() $r = 4,5, 6,10$
, every possible choice of
$r = 4,5, 6,10$
, every possible choice of
![]() $R^*$
had a triple
$R^*$
had a triple
![]() $(a,b,c) \in k_r^3$
which passed all of the imposed constraints, implying negative results for these r’s. For
$(a,b,c) \in k_r^3$
which passed all of the imposed constraints, implying negative results for these r’s. For
![]() $r = 8$
, the Hecke eigenvalue computation for the modular constraint was not feasible. For
$r = 8$
, the Hecke eigenvalue computation for the modular constraint was not feasible. For
![]() $r = 7,9$
, the size of
$r = 7,9$
, the size of
![]() $k_r$
was unfeasible (
$k_r$
was unfeasible (
![]() $\# k_r> 17 \times 10^6$
). However, there were choices of
$\# k_r> 17 \times 10^6$
). However, there were choices of
![]() $R^*$
such that sampling many
$R^*$
such that sampling many
![]() $(a,b,c) \in k_r^3$
at random for that
$(a,b,c) \in k_r^3$
at random for that
![]() $R^*$
did not yield a triple
$R^*$
did not yield a triple
![]() $(a,b,c)$
which passed all of the imposed constraints. It thus remains possible that the imposed constraints are in principle sufficient to give a positive result for some
$(a,b,c)$
which passed all of the imposed constraints. It thus remains possible that the imposed constraints are in principle sufficient to give a positive result for some
![]() $R^*$
’s for
$R^*$
’s for
![]() $r = 7, 9$
, but the method is infeasible computationally in its present form because
$r = 7, 9$
, but the method is infeasible computationally in its present form because
![]() $\# k_r$
is too large.
$\# k_r$
is too large.
3 Reciprocity constraints
In this section, we will prove the reciprocity constraint, which is used in the proof of Theorem 1.2. For this, we will use the following form of quadratic reciprocity over number fields and a corollary, both of which are taken from [Reference Chen and Siksek4].
Let L be a number field with ring of integers
![]() $\mathcal {O}_L$
. For an element or ideal of
$\mathcal {O}_L$
. For an element or ideal of
![]() $\mathcal {O}_L$
, we say that it is odd if it is coprime to
$\mathcal {O}_L$
, we say that it is odd if it is coprime to
![]() $2 \mathcal {O}_L$
.
$2 \mathcal {O}_L$
.
Theorem 3.1 Suppose
![]() $ L $
is a number field with r real embeddings. We write
$ L $
is a number field with r real embeddings. We write
![]() $\operatorname {\mathrm {sgn}}_{i}(\alpha )$
for the sign of the image of
$\operatorname {\mathrm {sgn}}_{i}(\alpha )$
for the sign of the image of
![]() $\alpha $
under the ith real embedding. Let
$\alpha $
under the ith real embedding. Let
![]() $\alpha , \lambda \in \mathcal {O}_L$
be integers with
$\alpha , \lambda \in \mathcal {O}_L$
be integers with
![]() $\alpha $
odd and
$\alpha $
odd and
![]() $\alpha $
and
$\alpha $
and
![]() $\lambda $
coprime. Decompose
$\lambda $
coprime. Decompose
![]() $\lambda \mathcal {O}_L = \mathfrak {L}\mathfrak {R}$
where
$\lambda \mathcal {O}_L = \mathfrak {L}\mathfrak {R}$
where
![]() $\mathfrak {R}$
is an odd ideal in
$\mathfrak {R}$
is an odd ideal in
![]() $\mathcal {O}_L$
and
$\mathcal {O}_L$
and
![]() $\mathfrak {L}$
is even. Suppose that
$\mathfrak {L}$
is even. Suppose that
![]() $\alpha $
is a quadratic residue modulo
$\alpha $
is a quadratic residue modulo
![]() $4\mathfrak {L}$
. Then
$4\mathfrak {L}$
. Then
where
![]() $\left (\frac {a}{\mathfrak {R}}\right )_{L}$
is the Jacobi symbol in L and
$\left (\frac {a}{\mathfrak {R}}\right )_{L}$
is the Jacobi symbol in L and
 $$\begin{align*}\sigma = \sum_{i=1}^{r} \frac{\operatorname{\mathrm{sgn}}_{i}(\alpha) - 1}{2}\frac{\operatorname{\mathrm{sgn}}_{i}(\lambda) - 1}{2}. \end{align*}$$
$$\begin{align*}\sigma = \sum_{i=1}^{r} \frac{\operatorname{\mathrm{sgn}}_{i}(\alpha) - 1}{2}\frac{\operatorname{\mathrm{sgn}}_{i}(\lambda) - 1}{2}. \end{align*}$$
For the definition of Jacobi symbol
![]() $\left (\frac {\lambda }{\mathfrak {R}}\right )_{L}$
over a number field L, see [Reference Chen and Siksek4] or [Reference Neukirch17, Definition 8.2]. Furthermore, for
$\left (\frac {\lambda }{\mathfrak {R}}\right )_{L}$
over a number field L, see [Reference Chen and Siksek4] or [Reference Neukirch17, Definition 8.2]. Furthermore, for
![]() $\alpha \in \mathcal {O}_L$
,
$\alpha \in \mathcal {O}_L$
,
![]() $\left (\frac {\lambda }{\alpha }\right )_{L} := \left (\frac {\lambda }{\alpha \mathcal {O}_L}\right )_{L}$
.
$\left (\frac {\lambda }{\alpha }\right )_{L} := \left (\frac {\lambda }{\alpha \mathcal {O}_L}\right )_{L}$
.
Corollary 3.2 Let
![]() $\alpha , \lambda $
be algebraic integers in the number field
$\alpha , \lambda $
be algebraic integers in the number field
![]() $ L $
with
$ L $
with
![]() $\alpha $
odd. Suppose that
$\alpha $
odd. Suppose that
![]() $\alpha \equiv \epsilon ^{2} \ \pmod {4\lambda }$
for some algebraic integer
$\alpha \equiv \epsilon ^{2} \ \pmod {4\lambda }$
for some algebraic integer
![]() $\epsilon $
in L. In addition, suppose that
$\epsilon $
in L. In addition, suppose that
![]() $\alpha $
is positive in every real embedding of
$\alpha $
is positive in every real embedding of
![]() $ L $
. Then
$ L $
. Then
Proof If
![]() $\alpha $
and
$\alpha $
and
![]() $\lambda $
are not coprime, the above symbol is zero. Otherwise, we are in the case where we can apply Theorem 3.1 in the case where
$\lambda $
are not coprime, the above symbol is zero. Otherwise, we are in the case where we can apply Theorem 3.1 in the case where
![]() $\mathfrak {L} = \lambda \mathcal {O}_{L}$
and
$\mathfrak {L} = \lambda \mathcal {O}_{L}$
and
![]() $\mathfrak {R} = \mathcal {O}_{L}$
. In this case,
$\mathfrak {R} = \mathcal {O}_{L}$
. In this case,
![]() $\sigma = 0$
since
$\sigma = 0$
since
![]() $\alpha $
is positive in every real embedding, and
$\alpha $
is positive in every real embedding, and
![]() ${\left (\frac {\alpha }{\mathcal {O}_{L}}\right )_L = 1}$
, so that
${\left (\frac {\alpha }{\mathcal {O}_{L}}\right )_L = 1}$
, so that
![]() ${\left (\frac {\lambda }{\alpha }\right )_L = 1}$
.
${\left (\frac {\lambda }{\alpha }\right )_L = 1}$
.
We also require the following lemmas.
Lemma 3.3 If
![]() $x, y \in \mathbb {R}$
satisfy
$x, y \in \mathbb {R}$
satisfy
![]() $x^n + y^n = 1$
for
$x^n + y^n = 1$
for
![]() $n \in \mathbb {N}$
, then
$n \in \mathbb {N}$
, then
![]() $xy < 1$
.
$xy < 1$
.
Proof For all real x, we have that
![]() $x^{2n} - x^{n} + 1> 0$
. This implies that
$x^{2n} - x^{n} + 1> 0$
. This implies that
![]() $x^{n}(1 - x^{n}) < 1$
. If
$x^{n}(1 - x^{n}) < 1$
. If
![]() $xy \ge 1$
, then we would have that
$xy \ge 1$
, then we would have that
![]() $x^n y^n = x^n (1-x^n) \ge 1$
, a contradiction. Hence, we conclude
$x^n y^n = x^n (1-x^n) \ge 1$
, a contradiction. Hence, we conclude
![]() $xy < 1$
.
$xy < 1$
.
Lemma 3.4 If
![]() $(a, b, c)$
is a primitive nontrivial solution to Fermat’s equation over K for some odd prime
$(a, b, c)$
is a primitive nontrivial solution to Fermat’s equation over K for some odd prime
![]() $p> 2$
, then
$p> 2$
, then
![]() $ab - c^{2}$
is negative in every real embedding of K.
$ab - c^{2}$
is negative in every real embedding of K.
Proof Let
![]() $\rho $
be any real embedding of K. Since
$\rho $
be any real embedding of K. Since
![]() $(a, b, c)$
is a primitive solution to the Fermat equation,
$(a, b, c)$
is a primitive solution to the Fermat equation,
![]() $(\rho (a), \rho (b), \rho (c))$
is also a primitive solution. Thus, if
$(\rho (a), \rho (b), \rho (c))$
is also a primitive solution. Thus, if
![]() $(a, b, c)$
is such a triple, then
$(a, b, c)$
is such a triple, then
 $$\begin{align*}{\bigg(\frac{\rho(a)}{-\rho(c)}\bigg)}^{p} + {\bigg(\frac{\rho(b)}{-\rho(c)}\bigg)}^{p} = 1. \end{align*}$$
$$\begin{align*}{\bigg(\frac{\rho(a)}{-\rho(c)}\bigg)}^{p} + {\bigg(\frac{\rho(b)}{-\rho(c)}\bigg)}^{p} = 1. \end{align*}$$
Now, we employ Lemma 3.3 to deduce
 $$\begin{align*}\frac{\rho(a)\rho(b)}{\rho(c)^{2}} < 1, \end{align*}$$
$$\begin{align*}\frac{\rho(a)\rho(b)}{\rho(c)^{2}} < 1, \end{align*}$$
which gives
![]() $\rho (ab - c^{2}) = \rho (a)(b) - \rho (c)^2 < 0$
.
$\rho (ab - c^{2}) = \rho (a)(b) - \rho (c)^2 < 0$
.
We now state and prove the reciprocity constraint.
Theorem 3.5 Let K be a number field, and let
![]() $\zeta _{r}$
be a primitive rth root of unity where
$\zeta _{r}$
be a primitive rth root of unity where
![]() $ (r,p) = 1 $
. If
$ (r,p) = 1 $
. If
![]() $r = 1$
, assume further that K has an even number of real embeddings. Let
$r = 1$
, assume further that K has an even number of real embeddings. Let
![]() $L = K(\zeta _{r})$
and write
$L = K(\zeta _{r})$
and write
![]() $\zeta _r = {\zeta ^{\prime }_{r}}^p $
where
$\zeta _r = {\zeta ^{\prime }_{r}}^p $
where
![]() $\zeta ^{\prime }_r$
is a primitive rth root of unity.
$\zeta ^{\prime }_r$
is a primitive rth root of unity.
If
![]() $(a,b,c)$
is a primitive solution over
$(a,b,c)$
is a primitive solution over
![]() $\mathcal {O}_K$
to
$\mathcal {O}_K$
to
and c is coprime to
![]() $2\mathcal {O}_{K}$
, then
$2\mathcal {O}_{K}$
, then
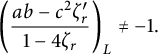 $$ \begin{align} \left(\frac{ab - c^{2}\zeta^{\prime}_{r}}{1 - 4\zeta_{r}}\right)_{L} \neq -1. \end{align} $$
$$ \begin{align} \left(\frac{ab - c^{2}\zeta^{\prime}_{r}}{1 - 4\zeta_{r}}\right)_{L} \neq -1. \end{align} $$
In particular, if
![]() $abc$
is coprime to
$abc$
is coprime to
![]() $2 \mathcal {O}_K$
, then (3.6) holds for all permutations of
$2 \mathcal {O}_K$
, then (3.6) holds for all permutations of
![]() $a,b,c$
.
$a,b,c$
.
Proof By assumption, c is coprime to
![]() $2\mathcal {O}_{K}$
. We employ the identity
$2\mathcal {O}_{K}$
. We employ the identity
Subtracting both sides of this identity by
![]() $c^{2p}(1 - 4\zeta _{r})$
, we get
$c^{2p}(1 - 4\zeta _{r})$
, we get
 $$ \begin{align} {(a^{p} - b^{p})}^{2} - c^{2p}(1 - 4\zeta_{r}) & = -4 \left( (ab)^p - \zeta_r c^{2p} \right) \\ \notag & = -4(ab -c^{2}\zeta^{\prime}_{r})h, \end{align} $$
$$ \begin{align} {(a^{p} - b^{p})}^{2} - c^{2p}(1 - 4\zeta_{r}) & = -4 \left( (ab)^p - \zeta_r c^{2p} \right) \\ \notag & = -4(ab -c^{2}\zeta^{\prime}_{r})h, \end{align} $$
where
Let
![]() $\alpha = 1 - 4\zeta _{r}$
and
$\alpha = 1 - 4\zeta _{r}$
and
![]() $\lambda = ab - c^{2} \zeta ^{\prime }_{r}$
. We first show that c is invertible modulo
$\lambda = ab - c^{2} \zeta ^{\prime }_{r}$
. We first show that c is invertible modulo
![]() $4\lambda = 4(ab - c^{2}\zeta ^{\prime }_{r})$
. To this end, let
$4\lambda = 4(ab - c^{2}\zeta ^{\prime }_{r})$
. To this end, let
![]() $\mathfrak {P}$
be a prime in
$\mathfrak {P}$
be a prime in
![]() $\mathcal {O}_{L}$
dividing c. We show that
$\mathcal {O}_{L}$
dividing c. We show that
![]() $\mathfrak {P}$
does not divide
$\mathfrak {P}$
does not divide
![]() $4\lambda $
. Indeed, suppose this were the case. Then
$4\lambda $
. Indeed, suppose this were the case. Then
![]() $\mathfrak {P}$
divides
$\mathfrak {P}$
divides
![]() $4\lambda $
and so either divides
$4\lambda $
and so either divides
![]() $4 \mathcal {O}_L$
or divides
$4 \mathcal {O}_L$
or divides
![]() $\lambda $
. Note that
$\lambda $
. Note that
![]() $\mathfrak {P}$
cannot divide
$\mathfrak {P}$
cannot divide
![]() $4 \mathcal {O}_L$
, for then
$4 \mathcal {O}_L$
, for then
![]() $\mathfrak {P}$
divides
$\mathfrak {P}$
divides
![]() $2 \mathcal {O}_L$
and thus
$2 \mathcal {O}_L$
and thus
![]() $c \in \mathfrak {P} \cap \mathcal {O}_{K}$
, contradicting that c is coprime to
$c \in \mathfrak {P} \cap \mathcal {O}_{K}$
, contradicting that c is coprime to
![]() $2 \mathcal {O}_K$
. Hence,
$2 \mathcal {O}_K$
. Hence,
![]() $\mathfrak {P} \mid \lambda $
. Then we have that
$\mathfrak {P} \mid \lambda $
. Then we have that
and so either a or b is in
![]() $\mathfrak {P}$
. However,
$\mathfrak {P}$
. However,
so
![]() $\mathfrak {P}$
divides
$\mathfrak {P}$
divides
![]() $a, b$
, and c. We have assumed that
$a, b$
, and c. We have assumed that
![]() $a, b, c$
are coprime in
$a, b, c$
are coprime in
![]() $\mathcal {O}_{K}$
. Let
$\mathcal {O}_{K}$
. Let
![]() $r_{1}, r_{2}, r_{3}$
be such that
$r_{1}, r_{2}, r_{3}$
be such that
Then we get the contradiction that
![]() $1 \in \mathfrak {P}$
.
$1 \in \mathfrak {P}$
.
In light of this, let
![]() $\epsilon \in \mathcal {O}_{L}$
be such that the image of
$\epsilon \in \mathcal {O}_{L}$
be such that the image of
![]() $\epsilon $
in
$\epsilon $
in
![]() $\mathcal {O}_{L}/(4(ab - c^{2}\zeta ^{\prime }_{r}))$
is
$\mathcal {O}_{L}/(4(ab - c^{2}\zeta ^{\prime }_{r}))$
is
We see that
![]() $\alpha $
is odd, for if
$\alpha $
is odd, for if
![]() $\mathfrak {P}$
divides both
$\mathfrak {P}$
divides both
![]() $\alpha $
and
$\alpha $
and
![]() $2 \mathcal {O}_L$
, then
$2 \mathcal {O}_L$
, then
![]() $\mathfrak {P}$
divides
$\mathfrak {P}$
divides
![]() $1$
, a contradiction. Then, from (3.7),
$1$
, a contradiction. Then, from (3.7),
Since L has no real embeddings if
![]() $r> 2$
, Corollary 3.2 gives the result in this case.
$r> 2$
, Corollary 3.2 gives the result in this case.
If
![]() $r = 2$
, we have that
$r = 2$
, we have that
![]() $\alpha = 5$
is positive in every real embedding of
$\alpha = 5$
is positive in every real embedding of
![]() $L = K$
because
$L = K$
because
![]() $\mathbb {Q}$
is fixed. Corollary 3.2 then gives the result in this case.
$\mathbb {Q}$
is fixed. Corollary 3.2 then gives the result in this case.
From Theorem 3.1, we have that
 $$\begin{align*}\left(\frac{ab - c^{2}}{-3}\right)_{K} = {(-1)}^{\sigma}. \end{align*}$$
$$\begin{align*}\left(\frac{ab - c^{2}}{-3}\right)_{K} = {(-1)}^{\sigma}. \end{align*}$$
We are under the assumption that K has an even number of real embeddings
![]() $2t$
so that
$2t$
so that
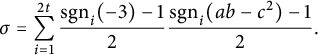 $$\begin{align*}\sigma = \sum_{i=1}^{2t} \frac{\operatorname{\mathrm{sgn}}_{i}(-3) - 1}{2}\frac{\operatorname{\mathrm{sgn}}_{i}(ab - c^{2}) - 1}{2}. \end{align*}$$
$$\begin{align*}\sigma = \sum_{i=1}^{2t} \frac{\operatorname{\mathrm{sgn}}_{i}(-3) - 1}{2}\frac{\operatorname{\mathrm{sgn}}_{i}(ab - c^{2}) - 1}{2}. \end{align*}$$
We see that
![]() $\operatorname {\mathrm {sgn}}_{i}(-3) = -1$
for all i. Lemma 3.4 gives that
$\operatorname {\mathrm {sgn}}_{i}(-3) = -1$
for all i. Lemma 3.4 gives that
![]() $ ab - c^{2} $
is totally negative and so
$ ab - c^{2} $
is totally negative and so
![]() $\operatorname {\mathrm {sgn}}_{i}(ab - c^{2}) = -1$
for all i and hence we conclude
$\operatorname {\mathrm {sgn}}_{i}(ab - c^{2}) = -1$
for all i and hence we conclude
![]() $\sigma = 2t $
is even. This gives the result for
$\sigma = 2t $
is even. This gives the result for
![]() $r = 1$
.
$r = 1$
.
4 Proof of Theorem 1.3
Let
![]() $K = \mathbb {Q}(\sqrt {17})$
, and let
$K = \mathbb {Q}(\sqrt {17})$
, and let
![]() $\mathcal {O}_K$
be its ring of integer, which has unique factorization. The prime
$\mathcal {O}_K$
be its ring of integer, which has unique factorization. The prime
![]() $2$
splits in K as
$2$
splits in K as
![]() $2 \mathcal {O}_K = \mathfrak {P}_1 \mathfrak {P}_2$
for prime ideals
$2 \mathcal {O}_K = \mathfrak {P}_1 \mathfrak {P}_2$
for prime ideals
![]() $\mathfrak {P}_1$
and
$\mathfrak {P}_1$
and
![]() $\mathfrak {P}_2$
of K. Suppose
$\mathfrak {P}_2$
of K. Suppose
![]() $(a,b,c)$
is a nontrivial primitive solution over
$(a,b,c)$
is a nontrivial primitive solution over
![]() $\mathcal {O}_K$
to (1.1), and let
$\mathcal {O}_K$
to (1.1), and let
![]() $E_0$
denote the Frey elliptic curve over K:
$E_0$
denote the Frey elliptic curve over K:
Proposition 4.2 Assume
![]() $p \ge 5$
. Up to scaling
$p \ge 5$
. Up to scaling
![]() $(a,b,c)$
by a unit in
$(a,b,c)$
by a unit in
![]() $\mathcal {O}_K$
, the conductor of
$\mathcal {O}_K$
, the conductor of
![]() $E_0$
over K is given by
$E_0$
over K is given by
Proof See [Reference Freitas and Siksek11, Corollary 5.1]. We note the fact that
![]() $\mathcal {O}_K$
has unique factorization means that there is no need to consider the extraneous prime
$\mathcal {O}_K$
has unique factorization means that there is no need to consider the extraneous prime
![]() $\mathfrak {r}$
in [Reference Freitas and Siksek11].
$\mathfrak {r}$
in [Reference Freitas and Siksek11].
We may assume that
since
![]() $a^p + b^p + c^p = 0$
implies that one of
$a^p + b^p + c^p = 0$
implies that one of
![]() $a^p,b^p,c^p$
is
$a^p,b^p,c^p$
is
![]() $0$
in the residue fields of
$0$
in the residue fields of
![]() $\mathfrak {P}_1$
and
$\mathfrak {P}_1$
and
![]() $\mathfrak {P}_2$
.
$\mathfrak {P}_2$
.
By the arguments in [Reference Freitas and Siksek11, p. 2], we need only prove Theorem 1.3 for
![]() $p \ge 17$
, which we now assume.
$p \ge 17$
, which we now assume.
Proposition 4.4 The Galois representation
![]() ${\overline {\rho }}_{E_0,p} : G_K \rightarrow \operatorname {GL}_2(\mathbb {F}_p)$
is irreducible if
${\overline {\rho }}_{E_0,p} : G_K \rightarrow \operatorname {GL}_2(\mathbb {F}_p)$
is irreducible if
![]() $p \ge 17$
.
$p \ge 17$
.
Proof See [Reference Freitas and Siksek11, Lemma 6.1, p. 9].
Proposition 4.5 There is a Hilbert newform f of trivial character, parallel weight
![]() $2$
, and level
$2$
, and level
![]() $\mathfrak {P}_1 \mathfrak {P}_2$
such that
$\mathfrak {P}_1 \mathfrak {P}_2$
such that
![]() ${\overline {\rho }}_{E_0,p} \simeq {\overline {\rho }}_{f,\mathfrak {p}}$
.
${\overline {\rho }}_{E_0,p} \simeq {\overline {\rho }}_{f,\mathfrak {p}}$
.
Proof The elliptic curve
![]() $E_0$
over K is modular by [Reference Freitas, LeHung and Siksek9]. Using [Reference Freitas and Siksek10, Theorem 7], we obtain the desired statement.
$E_0$
over K is modular by [Reference Freitas, LeHung and Siksek9]. Using [Reference Freitas and Siksek10, Theorem 7], we obtain the desired statement.
There is a unique Hilbert newform f of trivial character, parallel weight
![]() $2$
, and level
$2$
, and level
![]() $\mathfrak {P}_1\mathfrak {P}_2$
, and this corresponds to an elliptic curve E over K.
$\mathfrak {P}_1\mathfrak {P}_2$
, and this corresponds to an elliptic curve E over K.
Lemma 4.6 The elliptic curve E over K is given by
 $$ \begin{align*} E : Y^2 = X (X - (4 - \sqrt{17})) \left( X + \frac{-13+5 \sqrt{17}}{2} \right). \end{align*} $$
$$ \begin{align*} E : Y^2 = X (X - (4 - \sqrt{17})) \left( X + \frac{-13+5 \sqrt{17}}{2} \right). \end{align*} $$
Proof See [Reference Freitas and Siksek11, p. 13]. The conductor of E over K is
![]() $2 \mathcal {O}_K$
. Since E is modular, it corresponds to the unique Hilbert newform f of trivial character, parallel weight
$2 \mathcal {O}_K$
. Since E is modular, it corresponds to the unique Hilbert newform f of trivial character, parallel weight
![]() $2$
, and level
$2$
, and level
![]() $2 \mathcal {O}_K$
.
$2 \mathcal {O}_K$
.
Hence, we have that
by Proposition 4.5.
Proof of Theorem 1.3
Let
![]() $L = K(\zeta _r)$
where
$L = K(\zeta _r)$
where
![]() $\zeta _r$
is a primitive rth root of unity. We give two proofs in the cases
$\zeta _r$
is a primitive rth root of unity. We give two proofs in the cases
![]() $r = 1$
,
$r = 1$
,
![]() $r = 2$
, and
$r = 2$
, and
![]() $r = 3$
.
$r = 3$
.
-
(1) Case
 $r=1$
.
$r=1$
.Let
 $k = \mathcal {O}_K/3 \mathcal {O}_K \cong \mathbb {F}_9$
, noting that
$k = \mathcal {O}_K/3 \mathcal {O}_K \cong \mathbb {F}_9$
, noting that
 $\# k^\times = 8$
. Let
$\# k^\times = 8$
. Let
 $\mathfrak {q}_3 = 3 \mathcal {O}_K$
.
$\mathfrak {q}_3 = 3 \mathcal {O}_K$
.If
 $abc \notin k^\times $
or
$abc \notin k^\times $
or
 $a_{\mathfrak {q}_3}(E_0) \not = a_{\mathfrak {q}_3}(E)$
, then we obtain a bound on p similarly as in (2.9) and (2.11). This bound can be computed to be
$a_{\mathfrak {q}_3}(E_0) \not = a_{\mathfrak {q}_3}(E)$
, then we obtain a bound on p similarly as in (2.9) and (2.11). This bound can be computed to be
 $p \in \left \{ 2,3 \right \}$
.
$p \in \left \{ 2,3 \right \}$
.Assume from here on that
 $a,b,c \in k^\times $
and
$a,b,c \in k^\times $
and
 $a_{\mathfrak {q}_3}(E_0) = a_{\mathfrak {q}_3}(E)$
holds. For
$a_{\mathfrak {q}_3}(E_0) = a_{\mathfrak {q}_3}(E)$
holds. For
 $a,b, c \in k^\times $
, we set (4.8)
$a,b, c \in k^\times $
, we set (4.8) $$ \begin{align} \epsilon = a^p b^p c^{-2p} \text{ in } k. \end{align} $$
$$ \begin{align} \epsilon = a^p b^p c^{-2p} \text{ in } k. \end{align} $$
Since
 $p^2 \equiv 1 \ \pmod 8$
, we have that
$p^2 \equiv 1 \ \pmod 8$
, we have that
 $\epsilon ^R = ab c^{-2}$
in k where
$\epsilon ^R = ab c^{-2}$
in k where
 $R \equiv p \ \pmod 8$
. Hence, the condition (5.22) becomes (4.9)for all permutations of
$R \equiv p \ \pmod 8$
. Hence, the condition (5.22) becomes (4.9)for all permutations of $$ \begin{align} \left(\frac{\epsilon^R-1}{3}\right)_{K} \not= -1, \end{align} $$
$$ \begin{align} \left(\frac{\epsilon^R-1}{3}\right)_{K} \not= -1, \end{align} $$
 $a,b,c$
as (4.3) holds. We note that (5.20) holds as if not, by the left-hand side of (5.10), we would have that
$a,b,c$
as (4.3) holds. We note that (5.20) holds as if not, by the left-hand side of (5.10), we would have that
 $\sqrt {-3} \in K$
.
$\sqrt {-3} \in K$
.
Using
 $\mathsf{Magma}$
, we can check the set of triples
$\mathsf{Magma}$
, we can check the set of triples
 $(a,b,c) \in (k^\times )^3$
which satisfy and (4.11) for all permutations of
$(a,b,c) \in (k^\times )^3$
which satisfy and (4.11) for all permutations of $$ \begin{align*} a_{\mathfrak{q}_3}(E_0) = a_{\mathfrak{q}_3}(E), \end{align*} $$
$$ \begin{align*} a_{\mathfrak{q}_3}(E_0) = a_{\mathfrak{q}_3}(E), \end{align*} $$
 $a,b,c$
is empty if
$a,b,c$
is empty if
 $p \equiv 5, 7 \ \pmod {8}$
.
$p \equiv 5, 7 \ \pmod {8}$
.
-
(2) Case
 $r = 2$
.
$r = 2$
.Let
 $k = \mathcal {O}_K/5 \mathcal {O}_K \cong \mathbb {F}_{25}$
, noting that
$k = \mathcal {O}_K/5 \mathcal {O}_K \cong \mathbb {F}_{25}$
, noting that
 $\# k^\times = 24$
. Let
$\# k^\times = 24$
. Let
 $\mathfrak {q}_5 = 5 \mathcal {O}_K$
.
$\mathfrak {q}_5 = 5 \mathcal {O}_K$
.If
 $abc \notin k^\times $
or
$abc \notin k^\times $
or
 $a_{\mathfrak {q}_5}(E_0) \not = a_{\mathfrak {q}_5}(E)$
, then we obtain a bound on p similarly as in (2.9) and (2.11). This bound can be computed to be
$a_{\mathfrak {q}_5}(E_0) \not = a_{\mathfrak {q}_5}(E)$
, then we obtain a bound on p similarly as in (2.9) and (2.11). This bound can be computed to be
 $p \in \left \{ 2, 3, 5, 7 \right \}$
.
$p \in \left \{ 2, 3, 5, 7 \right \}$
.Assume from here on that
 $a,b,c \in k^\times $
and
$a,b,c \in k^\times $
and
 $a_{\mathfrak {q}_5}(E_0) = a_{\mathfrak {q}_5}(E)$
holds. For
$a_{\mathfrak {q}_5}(E_0) = a_{\mathfrak {q}_5}(E)$
holds. For
 $a,b, c \in k^\times $
, we set (4.10)
$a,b, c \in k^\times $
, we set (4.10) $$ \begin{align} \epsilon = a^p b^p c^{-2p} \text{ in } k. \end{align} $$
$$ \begin{align} \epsilon = a^p b^p c^{-2p} \text{ in } k. \end{align} $$
Since
 $p^2 \equiv 1 \ \pmod {24}$
, we have that
$p^2 \equiv 1 \ \pmod {24}$
, we have that
 $\epsilon ^R = ab c^{-2}$
in k where
$\epsilon ^R = ab c^{-2}$
in k where
 $R \equiv p \ \pmod {24}$
. Hence, the condition (5.22) becomes (4.11)for all permutations of
$R \equiv p \ \pmod {24}$
. Hence, the condition (5.22) becomes (4.11)for all permutations of $$ \begin{align} \left(\frac{\epsilon^R-1}{5}\right)_{K} \not= -1, \end{align} $$
$$ \begin{align} \left(\frac{\epsilon^R-1}{5}\right)_{K} \not= -1, \end{align} $$
 $a,b,c$
as (4.3) holds. We note that (5.20) holds as if not, by the left-hand side of (5.10), we would have that
$a,b,c$
as (4.3) holds. We note that (5.20) holds as if not, by the left-hand side of (5.10), we would have that
 $\sqrt {5} \in K$
.
$\sqrt {5} \in K$
.
Using
 $\mathsf{Magma}$
, we can check the set of triples
$\mathsf{Magma}$
, we can check the set of triples
 $(a,b,c) \in (k^\times )^3$
which satisfy and (4.11) for all permutations of
$(a,b,c) \in (k^\times )^3$
which satisfy and (4.11) for all permutations of $$ \begin{align*} a_{\mathfrak{q}_5}(E_0) = a_{\mathfrak{q}_5}(E), \end{align*} $$
$$ \begin{align*} a_{\mathfrak{q}_5}(E_0) = a_{\mathfrak{q}_5}(E), \end{align*} $$
 $a,b,c$
is empty if
$a,b,c$
is empty if
 $p \equiv 13, 17, 19, 23 \ \pmod {24}$
.
$p \equiv 13, 17, 19, 23 \ \pmod {24}$
.
-
(3) Case
 $r = 3$
.
$r = 3$
.Let
 $k = \mathcal {O}_K/21 \mathcal {O}_K \cong \mathbb {F}_9 \times \mathbb {F}_{49}$
, noting that
$k = \mathcal {O}_K/21 \mathcal {O}_K \cong \mathbb {F}_9 \times \mathbb {F}_{49}$
, noting that
 $\# k^\times = 384$
. Let
$\# k^\times = 384$
. Let
 $\mathfrak {q}_3 = 3 \mathcal {O}_K$
and
$\mathfrak {q}_3 = 3 \mathcal {O}_K$
and
 $\mathfrak {q}_7 = 7 \mathcal {O}_K$
.
$\mathfrak {q}_7 = 7 \mathcal {O}_K$
.If
 $abc \notin k^\times $
or one of the following two conditions holds, we obtain a bound on p similarly as in (2.9) and (2.11). This bound can be computed to be
$abc \notin k^\times $
or one of the following two conditions holds, we obtain a bound on p similarly as in (2.9) and (2.11). This bound can be computed to be $$ \begin{align*} a_{\mathfrak{q}_3}(E_0) & \not= a_{\mathfrak{q}_3}(E), \\ a_{\mathfrak{q}_7}(E_0) & \not= a_{\mathfrak{q}_7}(E), \end{align*} $$
$$ \begin{align*} a_{\mathfrak{q}_3}(E_0) & \not= a_{\mathfrak{q}_3}(E), \\ a_{\mathfrak{q}_7}(E_0) & \not= a_{\mathfrak{q}_7}(E), \end{align*} $$
 $p \in \left \{ 2,3,5,7 \right \}$
.
$p \in \left \{ 2,3,5,7 \right \}$
.
Assume from here on that
 $a,b,c \in k^\times $
and both hold. For
$a,b,c \in k^\times $
and both hold. For $$ \begin{align*} a_{\mathfrak{q}_3}(E_0) & = a_{\mathfrak{q}_3}(E) \quad \text{and} \\ a_{\mathfrak{q}_7}(E_0) & = a_{\mathfrak{q}_7}(E) \end{align*} $$
$$ \begin{align*} a_{\mathfrak{q}_3}(E_0) & = a_{\mathfrak{q}_3}(E) \quad \text{and} \\ a_{\mathfrak{q}_7}(E_0) & = a_{\mathfrak{q}_7}(E) \end{align*} $$
 $a,b,c \in k^\times $
, we set (4.12)
$a,b,c \in k^\times $
, we set (4.12) $$ \begin{align} \epsilon = a^p b^p c^{-2p} \text{ in } k. \end{align} $$
$$ \begin{align} \epsilon = a^p b^p c^{-2p} \text{ in } k. \end{align} $$
Let
 $R^*$
be the least positive residue such that
$R^*$
be the least positive residue such that
 $p \equiv R^* \ \pmod {384}$
, and let R be such that
$p \equiv R^* \ \pmod {384}$
, and let R be such that
 $R R^* \equiv 1 \ \pmod {384}$
. Then we have that
$R R^* \equiv 1 \ \pmod {384}$
. Then we have that
 $\epsilon ^R = ab c^{-2}$
in k. Hence, the condition (5.22), taking
$\epsilon ^R = ab c^{-2}$
in k. Hence, the condition (5.22), taking
 $\zeta _r' = \zeta _r^R$
since
$\zeta _r' = \zeta _r^R$
since
 $r = 3$
divides
$r = 3$
divides
 $384$
, becomes (4.13)for all permutations of
$384$
, becomes (4.13)for all permutations of $$ \begin{align} \left(\frac{\epsilon^R - \zeta_r'}{1- 4 \zeta_r}\right)_{K} \not= -1, \end{align} $$
$$ \begin{align} \left(\frac{\epsilon^R - \zeta_r'}{1- 4 \zeta_r}\right)_{K} \not= -1, \end{align} $$
 $a,b,c$
as (4.3) holds. We note that the hypothesis (5.20) holds as K is totally real.
$a,b,c$
as (4.3) holds. We note that the hypothesis (5.20) holds as K is totally real.
Using
 $\mathsf{Magma}$
, we can check the set of triples
$\mathsf{Magma}$
, we can check the set of triples
 $(a,b,c) \in (k^\times )^3$
which satisfy and (4.13) for all permutations of
$(a,b,c) \in (k^\times )^3$
which satisfy and (4.13) for all permutations of $$ \begin{align*} a_{\mathfrak{q}_3}(E_0) & = a_{\mathfrak{q}_3}(E), \\ a_{\mathfrak{q}_7}(E_0) & = a_{\mathfrak{q}_7}(E), \end{align*} $$
$$ \begin{align*} a_{\mathfrak{q}_3}(E_0) & = a_{\mathfrak{q}_3}(E), \\ a_{\mathfrak{q}_7}(E_0) & = a_{\mathfrak{q}_7}(E), \end{align*} $$
 $a,b,c$
is empty if
$a,b,c$
is empty if  $$ \begin{align*} & p \equiv 5, 7, 13, 23, 29, 31, 37, 47, 53, 55, 61, 71, 77, 79, 85, 95, 101, 103, \\ & 109, 119, 125, 127, 133, 143, 149, 151, 157, 167, 173, 175, 181, 191, 197, 199, 205, \\ & 215, 221, 223, 229, 239, 245, 247, 253, 263, 269, 271, 277, 287, 293, 295, 301, \\ & 311, 317, 319, 325, 335, 341, 343, 349, 359, 365, 367, 373, 383 \ \pmod{384}. \end{align*} $$
$$ \begin{align*} & p \equiv 5, 7, 13, 23, 29, 31, 37, 47, 53, 55, 61, 71, 77, 79, 85, 95, 101, 103, \\ & 109, 119, 125, 127, 133, 143, 149, 151, 157, 167, 173, 175, 181, 191, 197, 199, 205, \\ & 215, 221, 223, 229, 239, 245, 247, 253, 263, 269, 271, 277, 287, 293, 295, 301, \\ & 311, 317, 319, 325, 335, 341, 343, 349, 359, 365, 367, 373, 383 \ \pmod{384}. \end{align*} $$
It can be verified that the congruence condition above is equivalent to
 $p \equiv 5, 7, 13, 23 \ \pmod {24}$
, noting that
$p \equiv 5, 7, 13, 23 \ \pmod {24}$
, noting that
 $24$
divides
$24$
divides
 $384$
. Finally, the congruence
$384$
. Finally, the congruence
 $p \equiv 5, 7, 13, 23 \ \pmod {24}$
is equivalent to
$p \equiv 5, 7, 13, 23 \ \pmod {24}$
is equivalent to
 $p \equiv 5, 7 \ \pmod 8$
for prime
$p \equiv 5, 7 \ \pmod 8$
for prime
 $p \ge 5$
.
$p \ge 5$
.
Remark 4.14 We describe more specifically how Remark 2.17 applies to
![]() $d = 17$
: if
$d = 17$
: if
![]() $r = 4$
, we have that
$r = 4$
, we have that
![]() $(1-\zeta _4)\mathcal {O}_L = (\sqrt {17} \mathcal {O}_L)^2$
, so in a similar way as in (2.19), we obtain a trivial reciprocity constraint. For
$(1-\zeta _4)\mathcal {O}_L = (\sqrt {17} \mathcal {O}_L)^2$
, so in a similar way as in (2.19), we obtain a trivial reciprocity constraint. For
![]() $r = 6, 8$
, every possible choice of
$r = 6, 8$
, every possible choice of
![]() $R^*$
had a triple
$R^*$
had a triple
![]() $(a,b,c) \in k_r^3$
which passed all of the imposed constraints, implying a negative result. For
$(a,b,c) \in k_r^3$
which passed all of the imposed constraints, implying a negative result. For
![]() $r = 5, 7, 9, 10$
, the sizes of the
$r = 5, 7, 9, 10$
, the sizes of the
![]() $k_r$
’s were too large (
$k_r$
’s were too large (
![]() $\# k_r> 4\times 10^4$
). For
$\# k_r> 4\times 10^4$
). For
![]() $r = 5, 7, 9, 10$
, there were choices of
$r = 5, 7, 9, 10$
, there were choices of
![]() $R^*$
such that sampling many
$R^*$
such that sampling many
![]() $(a,b,c) \in k_r^3$
at random for that
$(a,b,c) \in k_r^3$
at random for that
![]() $R^*$
did not yield a triple
$R^*$
did not yield a triple
![]() $(a,b,c)$
which passed all of the imposed constraints. It thus remains possible that the imposed constraints are in principle sufficient to give a positive result for some
$(a,b,c)$
which passed all of the imposed constraints. It thus remains possible that the imposed constraints are in principle sufficient to give a positive result for some
![]() $R^*$
’s for
$R^*$
’s for
![]() $r = 5, 7, 9, 10$
, but the method is infeasible computationally in its present form because
$r = 5, 7, 9, 10$
, but the method is infeasible computationally in its present form because
![]() $\# k_r$
is too large.
$\# k_r$
is too large.
5 Reciprocity constraints using the Hilbert symbol
In this section, we use Hilbert symbols to prove a strengthened reciprocity constraint which does not have a condition on c.
Definition 5.1 For a global field L, we define the Hilbert symbol
![]() $( \cdot , \cdot )_L:L^{\times }\times L^{\times } \rightarrow \{-1,1\}$
as
$( \cdot , \cdot )_L:L^{\times }\times L^{\times } \rightarrow \{-1,1\}$
as
 $$ \begin{align} (a,b)_L := \begin{cases}1, &\text{ if }z^2 = ax^2 + by^2\text{ has a nontrivial solution in }L,\\ -1, &\text{ otherwise.}\end{cases} \end{align} $$
$$ \begin{align} (a,b)_L := \begin{cases}1, &\text{ if }z^2 = ax^2 + by^2\text{ has a nontrivial solution in }L,\\ -1, &\text{ otherwise.}\end{cases} \end{align} $$
Let
![]() $S_L$
denote the set of normalized places of L and partition them into
$S_L$
denote the set of normalized places of L and partition them into
 $$ \begin{align*} S_L^\infty & = \left\{ v \in S_L : v \mid \infty \right\}, \\ S_L^{\text{even}} & = \left\{ v \in S_L : v \mid 2 \right\}, \\ S_L^{\text{odd}} & = \left\{ v \in S_L : v \nmid 2 \right\}. \end{align*} $$
$$ \begin{align*} S_L^\infty & = \left\{ v \in S_L : v \mid \infty \right\}, \\ S_L^{\text{even}} & = \left\{ v \in S_L : v \mid 2 \right\}, \\ S_L^{\text{odd}} & = \left\{ v \in S_L : v \nmid 2 \right\}. \end{align*} $$
For a place
![]() $v \in S_L$
of L, we denote
$v \in S_L$
of L, we denote
![]() $(\alpha ,\beta )_v := (\alpha , \beta )_{L_v}$
, where
$(\alpha ,\beta )_v := (\alpha , \beta )_{L_v}$
, where
![]() $L_v$
is the completion of L at v. Let
$L_v$
is the completion of L at v. Let
![]() $\pi _v$
be a uniformizer for
$\pi _v$
be a uniformizer for
![]() $L_v$
, let
$L_v$
, let
![]() $\mathcal {O}_v$
be the ring of integers of
$\mathcal {O}_v$
be the ring of integers of
![]() $L_v$
, and let
$L_v$
, and let
![]() $\mathbb {F}_v$
be the residue field of
$\mathbb {F}_v$
be the residue field of
![]() $L_v$
.
$L_v$
.
We will state a few useful properties of the Hilbert symbol for later use.
Lemma 5.3 The Hilbert symbol defines a nondegenerate symmetric bimultiplicative pairing.
Proof See [Reference Voight21, Lemma 12.4.6].
Lemma 5.4 Let
![]() $a, b \in L^\times $
. Then the following hold:
$a, b \in L^\times $
. Then the following hold:
-
(1)
 $(a c^2,b d^2)_L = (a,b)_L$
for all
$(a c^2,b d^2)_L = (a,b)_L$
for all
 $c, d \in L^\times $
.
$c, d \in L^\times $
. -
(2)
 $(b,a)_L = (a,b)_L$
.
$(b,a)_L = (a,b)_L$
. -
(3)
 $(a,b)_L = (a,-ab)_L = (b,-ab)_L$
.
$(a,b)_L = (a,-ab)_L = (b,-ab)_L$
. -
(4)
 $(1,a)_L = (a,-a)_L = 1$
.
$(1,a)_L = (a,-a)_L = 1$
. -
(5) If
 $a \not = 1$
, then
$a \not = 1$
, then
 $(a, 1-a) = 1$
.
$(a, 1-a) = 1$
. -
(6) If
 $\sigma \in \mathrm{Aut}(L)$
, then
$\sigma \in \mathrm{Aut}(L)$
, then
 $(a,b)_L = (\sigma (a),\sigma (b))_L.$
$(a,b)_L = (\sigma (a),\sigma (b))_L.$
Proof See [Reference Voight21, Lemma 12.4.3].
Lemma 5.5 (Reciprocity law)
Let L be a number field, and let
![]() $S_L$
be the set of places of L. Then, for any
$S_L$
be the set of places of L. Then, for any
![]() $\alpha , \beta \in L^*$
, we have that
$\alpha , \beta \in L^*$
, we have that
Proof See [Reference Voight21, Corollary 14.6.2].
Lemma 5.7 With notation as above, let
![]() $q = \# \mathbb {F}_v$
be odd. Write
$q = \# \mathbb {F}_v$
be odd. Write
![]() $a = a_0 \pi_v ^{v(a)}$
and
$a = a_0 \pi_v ^{v(a)}$
and
![]() $b = b_0 \pi_v ^{v(b)}$
. Then we have that
$b = b_0 \pi_v ^{v(b)}$
. Then we have that
 $$ \begin{align} (a,b)_v = (-1)^{v(a) v(b) (q-1)/2} \genfrac(){}{}{a_0}{\pi_v}^{v(b)} \genfrac(){}{}{b_0}{\pi_v}^{v(a)}. \end{align} $$
$$ \begin{align} (a,b)_v = (-1)^{v(a) v(b) (q-1)/2} \genfrac(){}{}{a_0}{\pi_v}^{v(b)} \genfrac(){}{}{b_0}{\pi_v}^{v(a)}. \end{align} $$
Proof See [Reference Voight21, equation (12.4.10)].
We now move on to the theorem that enables us to tackle the reciprocity constraint on the primitive solutions over
![]() $\mathbb {Q}(\sqrt {17})$
. The following is a generalization of [Reference Bennett, Chen, Dahmen and Yazdani1, Proposition 17].
$\mathbb {Q}(\sqrt {17})$
. The following is a generalization of [Reference Bennett, Chen, Dahmen and Yazdani1, Proposition 17].
Theorem 5.9 Let L be a number field containing a primitive rth root of unity
![]() $\zeta _r$
such that
$\zeta _r$
such that
![]() $(r,n) = 1$
where
$(r,n) = 1$
where
![]() $n \in \mathbb {N}$
. Assume
$n \in \mathbb {N}$
. Assume
![]() $s, t \in \mathcal {O}_L$
,
$s, t \in \mathcal {O}_L$
,
![]() $v(t) = 0$
for all
$v(t) = 0$
for all
![]() $v \in S_L$
such that
$v \in S_L$
such that
![]() $v(n)> 0$
, and
$v(n)> 0$
, and
![]() $v(s)> 0$
only for places
$v(s)> 0$
only for places
![]() $v \in \mathrm{S}_\mathrm{L}^{\mathrm {even}}$
. Furthermore, suppose we have the following identity:
$v \in \mathrm{S}_\mathrm{L}^{\mathrm {even}}$
. Furthermore, suppose we have the following identity:
for coprime
![]() $A, B, C \in \mathcal {O}_L$
and write
$A, B, C \in \mathcal {O}_L$
and write
![]() $\zeta _r = {\zeta _r'}^n$
where
$\zeta _r = {\zeta _r'}^n$
where
![]() $\zeta _r'$
is a primitive rth root of unity.
$\zeta _r'$
is a primitive rth root of unity.
Then we have that
Proof The hypotheses imply that
![]() $s, t, (C^n - \zeta _r B^{2n})$
are nonzero, and hence also
$s, t, (C^n - \zeta _r B^{2n})$
are nonzero, and hence also
![]() $(C - \zeta _r' B^2) \not = 0$
, so the Hilbert symbols used below are well defined. Note that
$(C - \zeta _r' B^2) \not = 0$
, so the Hilbert symbols used below are well defined. Note that
for all
![]() $v \in S_{L}$
because
$v \in S_{L}$
because
Using the fact that
![]() $\zeta _r = {\zeta _r'}^n$
and the factorization
$\zeta _r = {\zeta _r'}^n$
and the factorization
 $$ \begin{align} C^{n} - \zeta_{r}B^{2n} &= C^n - (\zeta_r' B^2)^n\\ \notag &= (C - \zeta_{r}' B^{2})(C^{n-1} + C^{n-2} \zeta_{r}' B^{2} + \cdots + (\zeta_r' B^2)^{n-1}), \end{align} $$
$$ \begin{align} C^{n} - \zeta_{r}B^{2n} &= C^n - (\zeta_r' B^2)^n\\ \notag &= (C - \zeta_{r}' B^{2})(C^{n-1} + C^{n-2} \zeta_{r}' B^{2} + \cdots + (\zeta_r' B^2)^{n-1}), \end{align} $$
we see that
using Lemma 5.3.
Let
![]() $\beta = s(C - \zeta _{r}'B^{2})$
. By (5.6), we have that
$\beta = s(C - \zeta _{r}'B^{2})$
. By (5.6), we have that
Thus, it suffices to show that
![]() $(t, \beta )_{v} = 1$
when
$(t, \beta )_{v} = 1$
when
![]() $v \in S_{L}^{\mathrm {odd}}$
and
$v \in S_{L}^{\mathrm {odd}}$
and
![]() $v(t)$
is even.
$v(t)$
is even.
Suppose
![]() $v \in S_{L}^{\mathrm {odd}}$
and
$v \in S_{L}^{\mathrm {odd}}$
and
![]() $v(t)$
is even. By (5.8),
$v(t)$
is even. By (5.8),
![]() $(t, \beta )_{v} = 1$
when
$(t, \beta )_{v} = 1$
when
![]() $v(\beta )$
is even. So suppose that
$v(\beta )$
is even. So suppose that
![]() $v(\beta )$
is odd.
$v(\beta )$
is odd.
If
![]() $v(n)> 0$
, then we have that
$v(n)> 0$
, then we have that
![]() $v(t) = 0$
by assumption. As
$v(t) = 0$
by assumption. As
![]() $ v(\beta ) $
is odd, we deduce from (5.10) and (5.12) that
$ v(\beta ) $
is odd, we deduce from (5.10) and (5.12) that
so that
Since
![]() $A, B, C$
are coprime, by (5.10), we deduce that A and B are coprime, as
$A, B, C$
are coprime, by (5.10), we deduce that A and B are coprime, as
![]() $v(A), v(B)> 0$
implies
$v(A), v(B)> 0$
implies
![]() $v(s C^n)> 0$
. Since
$v(s C^n)> 0$
. Since
![]() $v(s) = 0$
, we see that
$v(s) = 0$
, we see that
![]() $v(C)> 0$
, contradicting
$v(C)> 0$
, contradicting
![]() $A, B, C$
being coprime. Hence, if
$A, B, C$
being coprime. Hence, if
![]() $v(B)> 0$
, then by (5.15) we obtain that
$v(B)> 0$
, then by (5.15) we obtain that
![]() $v(A)> 0$
, contradicting
$v(A)> 0$
, contradicting
![]() $A, B $
being coprime. Thus,
$A, B $
being coprime. Thus,
![]() $v(B) = 0$
and B is a v-adic unit. From (5.15), we deduce that
$v(B) = 0$
and B is a v-adic unit. From (5.15), we deduce that
and hence
using also that
![]() $v(t) = 0$
. Using Lemma 5.7, this leads to
$v(t) = 0$
. Using Lemma 5.7, this leads to
![]() $(t, \beta ) = 1$
.
$(t, \beta ) = 1$
.
If
![]() $v(n) = 0$
, then since
$v(n) = 0$
, then since
![]() $v(\beta )$
is odd and
$v(\beta )$
is odd and
![]() $v(s) = 0$
, we firstly have that
$v(s) = 0$
, we firstly have that
We have that
![]() $v(C) = 0$
for if
$v(C) = 0$
for if
![]() $v(C)> 0$
, then by (5.16)
$v(C)> 0$
, then by (5.16)
![]() $v(B)> 0$
and hence by (5.10)
$v(B)> 0$
and hence by (5.10)
![]() $v(A)> 0$
, contradicting that
$v(A)> 0$
, contradicting that
![]() $A, B, C$
are coprime. It follows that
$A, B, C$
are coprime. It follows that
which from the conditions
![]() $v(n) = v(C) = 0$
imply that
$v(n) = v(C) = 0$
imply that
Since
![]() $v(t)$
is even, using Lemma 5.7, it follows that
$v(t)$
is even, using Lemma 5.7, it follows that
![]() $(t, C^{n-1} + \cdots + (\zeta _r' B^2)^{n-1})_{v} = 1$
. Hence, by (5.13), we obtain
$(t, C^{n-1} + \cdots + (\zeta _r' B^2)^{n-1})_{v} = 1$
. Hence, by (5.13), we obtain
as desired.
Remark 5.17 In our application,
![]() $L = K(\zeta _r)$
,
$L = K(\zeta _r)$
,
![]() $n = p$
,
$n = p$
,
![]() $t = 1 - 4 \zeta _r$
,
$t = 1 - 4 \zeta _r$
,
![]() $s = 4$
,
$s = 4$
,
![]() $C = ab, B = c, A = a^p-b^p$
, and we have the identity (5.10) because of (3.7). Here,
$C = ab, B = c, A = a^p-b^p$
, and we have the identity (5.10) because of (3.7). Here,
![]() $v(s)> 0$
only for places
$v(s)> 0$
only for places
![]() $v \in S_L^{\text {even}}$
and
$v \in S_L^{\text {even}}$
and
![]() $A,B,C$
are coprime. Finally, we require
$A,B,C$
are coprime. Finally, we require
![]() $(p)$
to be coprime to
$(p)$
to be coprime to
![]() $(t) = (1 - 4 \zeta _r)$
to ensure the hypothesis
$(t) = (1 - 4 \zeta _r)$
to ensure the hypothesis
![]() $v(t) = 0$
for all
$v(t) = 0$
for all
![]() $v \in S_L$
such that
$v \in S_L$
such that
![]() $v(n)> 0$
.
$v(n)> 0$
.
We need a few more lemmas to aid the proof of our reciprocity constraint.
Lemma 5.18 Let L be a number field containing a primitive rth root of unity
![]() $\zeta _r$
, and L is unramified at
$\zeta _r$
, and L is unramified at
![]() $2$
. Let v be a place of L above
$2$
. Let v be a place of L above
![]() $2$
. Then
$2$
. Then
![]() $(1 - 4 \zeta _r,b)_v = 1$
for any
$(1 - 4 \zeta _r,b)_v = 1$
for any
![]() $b \in L$
with
$b \in L$
with
![]() $v(b) = 0$
.
$v(b) = 0$
.
Proof The proof in [Reference Serre18, Theorem 1, Chapter III, Section 1.2] for the case
![]() $L = \mathbb {Q}$
and
$L = \mathbb {Q}$
and
![]() $\alpha = \beta = 0$
can be adapted to prove this lemma.
$\alpha = \beta = 0$
can be adapted to prove this lemma.
If u and b are elements in
![]() $L_v^{\times }$
with
$L_v^{\times }$
with
![]() $u \equiv 1 \ \pmod {8}$
, then we first show that
$u \equiv 1 \ \pmod {8}$
, then we first show that
where the Hilbert symbol is taken in
![]() $L_{v}$
. Indeed, if
$L_{v}$
. Indeed, if
![]() $u \equiv 1 \ \pmod {8}$
, then since
$u \equiv 1 \ \pmod {8}$
, then since
applying Hensel’s lemma to
![]() $f(x) = x^{2} - u $
, we see that u is a square in
$f(x) = x^{2} - u $
, we see that u is a square in
![]() $L_v$
, say
$L_v$
, say
![]() $u = a^{2}$
. Hence,
$u = a^{2}$
. Hence,
so
![]() $(u, b)_v = 1$
.
$(u, b)_v = 1$
.
Now, let
![]() $k_v$
be the residue field of
$k_v$
be the residue field of
![]() $L_v$
, and let
$L_v$
, and let
![]() $u = 1 - 4 \zeta _r$
. Since
$u = 1 - 4 \zeta _r$
. Since
![]() $k_v^\times $
is odd, we can solve the equation
$k_v^\times $
is odd, we can solve the equation
![]() $b x^2 = \zeta _r$
in
$b x^2 = \zeta _r$
in
![]() $k_v^\times $
for
$k_v^\times $
for
![]() $x \in k_v^\times $
. Then
$x \in k_v^\times $
. Then
![]() $u(1)^2 + b (2x)^2 \equiv 1 \ \pmod 8$
and hence
$u(1)^2 + b (2x)^2 \equiv 1 \ \pmod 8$
and hence
![]() $u(1)^2 + b (2x)^2 = a^2$
for some
$u(1)^2 + b (2x)^2 = a^2$
for some
![]() $a \in L_v$
by the argument above. It follows then that
$a \in L_v$
by the argument above. It follows then that
![]() $(u,b)_v = (1 - 4 \zeta _r, b) = 1$
.
$(u,b)_v = (1 - 4 \zeta _r, b) = 1$
.
The following is a strengthened version of Theorem 3.5, now with no condition on c being coprime to
![]() $2 \mathcal {O}_K$
.
$2 \mathcal {O}_K$
.
Theorem 5.19 Let
![]() $K $
be a number field, and let
$K $
be a number field, and let
![]() $L = K(\zeta _{r})$
where
$L = K(\zeta _{r})$
where
![]() $\zeta _{r}$
be a primitive rth root of unity such that
$\zeta _{r}$
be a primitive rth root of unity such that
![]() $(r,p) = 1$
. If
$(r,p) = 1$
. If
![]() $r = 1$
, assume further that K has an even number of real embeddings.
$r = 1$
, assume further that K has an even number of real embeddings.
Suppose L is unramified at
![]() $2$
, K is totally split at
$2$
, K is totally split at
![]() $2$
,
$2$
,
![]() $(p)$
is coprime to
$(p)$
is coprime to
![]() $(1 - 4 \zeta _r)$
, and write
$(1 - 4 \zeta _r)$
, and write
![]() $\zeta _{r} = \zeta _r^{{\prime }p}$
where
$\zeta _{r} = \zeta _r^{{\prime }p}$
where
![]() $\zeta _r'$
is a primitive rth root of unity.
$\zeta _r'$
is a primitive rth root of unity.
If
![]() $(a,b,c)$
is a primitive solution over
$(a,b,c)$
is a primitive solution over
![]() $\mathcal {O}_K$
to
$\mathcal {O}_K$
to
such that
then one has
 $$ \begin{align} \left(\frac{ab - c^{2}\zeta^{\prime}_{r}}{1 - 4\zeta_{r}}\right)_{L} \neq -1, \end{align} $$
$$ \begin{align} \left(\frac{ab - c^{2}\zeta^{\prime}_{r}}{1 - 4\zeta_{r}}\right)_{L} \neq -1, \end{align} $$
for all permutations of
![]() $a,b,c$
.
$a,b,c$
.
Proof We may assume that
![]() $ab-c^2\zeta _r^{\prime }$
and
$ab-c^2\zeta _r^{\prime }$
and
![]() $1-4\zeta _r$
are coprime, or else we are already done as we would have
$1-4\zeta _r$
are coprime, or else we are already done as we would have
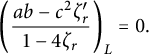 $$ \begin{align*} \left(\frac{ab - c^{2}\zeta^{\prime}_{r}}{1 - 4\zeta_{r}}\right)_{L} = 0. \end{align*} $$
$$ \begin{align*} \left(\frac{ab - c^{2}\zeta^{\prime}_{r}}{1 - 4\zeta_{r}}\right)_{L} = 0. \end{align*} $$
Since
![]() $1 - 4 \zeta _r$
is coprime to
$1 - 4 \zeta _r$
is coprime to
![]() $2 \mathcal {O}_L$
, we have from the definition of Jacobi (see, for instance, [Reference Neukirch17, Definition 8.2]) symbol that
$2 \mathcal {O}_L$
, we have from the definition of Jacobi (see, for instance, [Reference Neukirch17, Definition 8.2]) symbol that
 $$ \begin{align} \left(\frac{ab - c^{2}\zeta^{\prime}_{r}}{1 - 4\zeta_{r}}\right)_{L} = \prod_{v \in S_{L}^{\mathrm{odd}}, v(1 - 4 \zeta_r) \text{ odd}} {\left(\frac{ab-c^2 \zeta_r'}{\pi_v}\right)^{v(1-4\zeta_r)}}. \end{align} $$
$$ \begin{align} \left(\frac{ab - c^{2}\zeta^{\prime}_{r}}{1 - 4\zeta_{r}}\right)_{L} = \prod_{v \in S_{L}^{\mathrm{odd}}, v(1 - 4 \zeta_r) \text{ odd}} {\left(\frac{ab-c^2 \zeta_r'}{\pi_v}\right)^{v(1-4\zeta_r)}}. \end{align} $$
We note that the product is by definition over the
![]() $v \in S_{L}^{\mathrm {odd}}$
, but only the terms with
$v \in S_{L}^{\mathrm {odd}}$
, but only the terms with
![]() $v(1-4\zeta _r)$
odd can be
$v(1-4\zeta _r)$
odd can be
![]() $-1$
. Using Lemma 5.7, we see that
$-1$
. Using Lemma 5.7, we see that
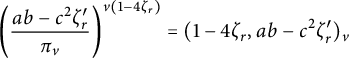 $$ \begin{align*} {\left(\frac{ab-c^2 \zeta_r'}{\pi_v}\right)^{v(1-4\zeta_r)}} = (1 - 4 \zeta_r, ab-c^2 \zeta_r')_v \end{align*} $$
$$ \begin{align*} {\left(\frac{ab-c^2 \zeta_r'}{\pi_v}\right)^{v(1-4\zeta_r)}} = (1 - 4 \zeta_r, ab-c^2 \zeta_r')_v \end{align*} $$
if
![]() $v \in S_{L}^{\mathrm {odd}}$
,
$v \in S_{L}^{\mathrm {odd}}$
,
![]() $v(1-4\zeta _r)$
is odd, and
$v(1-4\zeta _r)$
is odd, and
![]() $v(ab-c^2\zeta _r') = 0$
. Hence, we obtain that
$v(ab-c^2\zeta _r') = 0$
. Hence, we obtain that
 $$ \begin{align} \left(\frac{ab - c^{2}\zeta^{\prime}_{r}}{1 - 4\zeta_{r}}\right)_{L} = \prod_{v \in S_{L}^{\mathrm{odd}}, v(1-4\zeta_r) \text{ odd}} (1 - 4 \zeta_r, ab - c^2 \zeta_r')_v. \end{align} $$
$$ \begin{align} \left(\frac{ab - c^{2}\zeta^{\prime}_{r}}{1 - 4\zeta_{r}}\right)_{L} = \prod_{v \in S_{L}^{\mathrm{odd}}, v(1-4\zeta_r) \text{ odd}} (1 - 4 \zeta_r, ab - c^2 \zeta_r')_v. \end{align} $$
As
![]() $(a,b,c)$
is primitive, for any
$(a,b,c)$
is primitive, for any
![]() $v \in S_{L}^{\mathrm {even}}$
, two of the elements
$v \in S_{L}^{\mathrm {even}}$
, two of the elements
![]() $a,b,c$
are units in
$a,b,c$
are units in
![]() $\mathcal {O}_{L,v}$
and the remaining element has positive valuation, since
$\mathcal {O}_{L,v}$
and the remaining element has positive valuation, since
![]() $a, b, c \in \mathcal {O}_K$
and K is totally split at
$a, b, c \in \mathcal {O}_K$
and K is totally split at
![]() $2$
. This implies that
$2$
. This implies that
is coprime to
![]() $2 \mathcal {O}_L$
. By Lemma 5.18, it follows that
$2 \mathcal {O}_L$
. By Lemma 5.18, it follows that
for all
![]() $v \in S_{L}^{\mathrm {even}}$
as we are assuming L is unramified at
$v \in S_{L}^{\mathrm {even}}$
as we are assuming L is unramified at
![]() $2$
.
$2$
.
If
![]() $r \ge 3$
, then L is totally complex and we have that
$r \ge 3$
, then L is totally complex and we have that
![]() $(1-4 \zeta _r, ab - c^2 \zeta _r')_v = 1$
for all
$(1-4 \zeta _r, ab - c^2 \zeta _r')_v = 1$
for all
![]() $v \in S_L^\infty $
.
$v \in S_L^\infty $
.
If
![]() $r = 2$
, then
$r = 2$
, then
![]() $L = K$
and
$L = K$
and
![]() $1 - 4 \zeta _r = 5$
is positive in every real embedding of L. Thus,
$1 - 4 \zeta _r = 5$
is positive in every real embedding of L. Thus,
![]() $(1-4 \zeta _r, ab - c^2 \zeta _r')_v = 1$
for all
$(1-4 \zeta _r, ab - c^2 \zeta _r')_v = 1$
for all
![]() $v \in S_L^\infty $
.
$v \in S_L^\infty $
.
If
![]() $r = 1$
, then
$r = 1$
, then
![]() $L = K$
is a number field with an even number of real embeddings by hypothesis. Thus, using Lemma 3.4, we obtain that
$L = K$
is a number field with an even number of real embeddings by hypothesis. Thus, using Lemma 3.4, we obtain that
as the Hilbert symbols which are
![]() $-1$
occur in total an even number of times in the above product.
$-1$
occur in total an even number of times in the above product.
Thus, in all cases for r, using Theorem 5.9, we see that the third product in (5.11) is
![]() $1$
, which implies that
$1$
, which implies that
 $$ \begin{align*}\left(\frac{ab - c^{2}\zeta^{\prime}_{r}}{1 - 4\zeta_{r}}\right)_{L} = 1.\end{align*} $$
$$ \begin{align*}\left(\frac{ab - c^{2}\zeta^{\prime}_{r}}{1 - 4\zeta_{r}}\right)_{L} = 1.\end{align*} $$
The hypothesis (5.20) ensures that the quantity in (5.10) is nonzero.
Remark 5.24 The constraint in (5.11) of Theorem 5.9 is an example of a Brauer–Manin obstruction. Let
![]() $\mathcal {A}$
be the Azumaya algebra given by the Hilbert symbol
$\mathcal {A}$
be the Azumaya algebra given by the Hilbert symbol
![]() $(t, s (C - \zeta _r' B^2))$
on the variety defined by (5.10), subject to
$(t, s (C - \zeta _r' B^2))$
on the variety defined by (5.10), subject to
![]() $A, B, C$
coprime and
$A, B, C$
coprime and
![]() $C^n - \zeta _r B^{2n} \not = 0$
. Then (5.14), which is used in the proof of (5.11), corresponds to the condition
$C^n - \zeta _r B^{2n} \not = 0$
. Then (5.14), which is used in the proof of (5.11), corresponds to the condition
of the first formula in the introduction of [Reference Bright2].
6 Essential obstructive S-unit solutions
Let
![]() $K = \mathbb {Q}(\sqrt {5})$
or
$K = \mathbb {Q}(\sqrt {5})$
or
![]() $K = \mathbb {Q}(\sqrt {17})$
, and let S be the set of places of K above
$K = \mathbb {Q}(\sqrt {17})$
, and let S be the set of places of K above
![]() $2$
.
$2$
.
Suppose
![]() $(a,b,c) \in \mathcal {O}_K^3$
is a nontrivial primitive solution to (1.1) with
$(a,b,c) \in \mathcal {O}_K^3$
is a nontrivial primitive solution to (1.1) with
![]() $p = 1$
, that is,
$p = 1$
, that is,
If the Frey curve
is an elliptic curve over K with conductor
![]() $N = 8 \mathcal {O}_K$
for
$N = 8 \mathcal {O}_K$
for
![]() $K = \mathbb {Q}(\sqrt {5})$
and conductor
$K = \mathbb {Q}(\sqrt {5})$
and conductor
![]() $N = 2 \mathcal {O}_K$
for
$N = 2 \mathcal {O}_K$
for
![]() $K = \mathbb {Q}(\sqrt {17})$
, then the triple
$K = \mathbb {Q}(\sqrt {17})$
, then the triple
![]() $(a,b,c)$
poses an obstruction to solving (1.1) over K using the modular method. We call such a triple
$(a,b,c)$
poses an obstruction to solving (1.1) over K using the modular method. We call such a triple
![]() $(a,b,c)$
an (essential) obstructive solution to (1.1). Given such a triple
$(a,b,c)$
an (essential) obstructive solution to (1.1). Given such a triple
![]() $(a,b,c)$
, multiplication by the square of a unit in
$(a,b,c)$
, multiplication by the square of a unit in
![]() $\mathcal {O}_K$
produces another such triple with
$\mathcal {O}_K$
produces another such triple with
![]() $E_{a,b,c}$
in the same isomorphism class over K, and thus it is natural to consider obstructive solutions
$E_{a,b,c}$
in the same isomorphism class over K, and thus it is natural to consider obstructive solutions
![]() $(a,b,c)$
up to multiplication by the square of a unit in
$(a,b,c)$
up to multiplication by the square of a unit in
![]() $\mathcal {O}_K$
.
$\mathcal {O}_K$
.
If
![]() $(a,b,c)$
is an obstructive solution to (1.1), it can be seen that division by any one of
$(a,b,c)$
is an obstructive solution to (1.1), it can be seen that division by any one of
![]() $-a,-b,-c$
in (6.1) gives a solution to the S-unit equation
$-a,-b,-c$
in (6.1) gives a solution to the S-unit equation
where
![]() $U, V$
are S-units in K. Conversely, given a solution
$U, V$
are S-units in K. Conversely, given a solution
![]() $(U,V)$
to the S-unit equation, we can form a triple from the six orderings of
$(U,V)$
to the S-unit equation, we can form a triple from the six orderings of
![]() $U, V,-1$
and scale by an element of
$U, V,-1$
and scale by an element of
![]() $K^*$
to produce a primitive solution
$K^*$
to produce a primitive solution
![]() $(a,b,c) \in \mathcal {O}_K^3$
to (6.1). However, the possible triples
$(a,b,c) \in \mathcal {O}_K^3$
to (6.1). However, the possible triples
![]() $(a,b,c)$
which arise need not be obstructive solutions, so not all solutions to the S-unit equation (6.2) are relevant as obstructions to the modular method.
$(a,b,c)$
which arise need not be obstructive solutions, so not all solutions to the S-unit equation (6.2) are relevant as obstructions to the modular method.
In this section, we give methods to list the obstructive solutions
![]() $(a,b,c)$
to (1.1). This serves two purposes: first, it gives a more detailed description of the obstructions to solving Fermat’s Last Theorem over these quadratic fields, and second it gives a double check on the computations used to prove the main results of this paper.
$(a,b,c)$
to (1.1). This serves two purposes: first, it gives a more detailed description of the obstructions to solving Fermat’s Last Theorem over these quadratic fields, and second it gives a double check on the computations used to prove the main results of this paper.
One method to list the obstructive solutions
![]() $(a,b,c)$
to (1.1) would be to compute the solutions to the S-unit equation (6.2) for K. This can be done in a few minutes in
$(a,b,c)$
to (1.1) would be to compute the solutions to the S-unit equation (6.2) for K. This can be done in a few minutes in
![]() $\mathtt { SageMath}$
. However, a direct computation of solutions to the S-unit equation for
$\mathtt { SageMath}$
. However, a direct computation of solutions to the S-unit equation for
![]() $\mathbb {Q}(\sqrt {17})$
using
$\mathbb {Q}(\sqrt {17})$
using
![]() $\mathsf{SageMath}$
is slow and does not appear to terminate in any reasonable amount of time.
$\mathsf{SageMath}$
is slow and does not appear to terminate in any reasonable amount of time.
We explain now an alternate method of determining obstructive solutions
![]() $(a,b,c)$
to (1.1) using known lists of elliptic curves over K with conductor N [20].
$(a,b,c)$
to (1.1) using known lists of elliptic curves over K with conductor N [20].
First, recall that if we have two elliptic curves
![]() $E_1$
and
$E_1$
and
![]() $E_2$
over K, given in the following form,
$E_2$
over K, given in the following form,
 $$ \begin{align*} E_1 : y_1^2 = f_1(x_1), \\ E_2 : y_2^2 = f_2(x_2), \end{align*} $$
$$ \begin{align*} E_1 : y_1^2 = f_1(x_1), \\ E_2 : y_2^2 = f_2(x_2), \end{align*} $$
where
![]() $f_i \in \mathcal {O}_K[x]$
are monic of degree
$f_i \in \mathcal {O}_K[x]$
are monic of degree
![]() $3$
, then
$3$
, then
![]() $E_1$
is isomorphic to
$E_1$
is isomorphic to
![]() $E_2$
over K if and only if there exist
$E_2$
over K if and only if there exist
![]() $u, \beta \in \mathcal {O}_K$
and a change of variables
$u, \beta \in \mathcal {O}_K$
and a change of variables
Suppose
![]() $(a,b,c)$
is an obstructive solution to (1.1). Then the elliptic curve
$(a,b,c)$
is an obstructive solution to (1.1). Then the elliptic curve
satisfies
for some elliptic curve E defined over K of conductor equal to N. Due to primitivity of
![]() $(a,b,c)$
, (6.6) is semistable at primes
$(a,b,c)$
, (6.6) is semistable at primes
![]() $\mathfrak {q}$
of K coprime to
$\mathfrak {q}$
of K coprime to
![]() $2 \mathcal {O}_K$
, and hence already a local minimal Weierstrass model at such
$2 \mathcal {O}_K$
, and hence already a local minimal Weierstrass model at such
![]() $\mathfrak {q}$
. Since
$\mathfrak {q}$
. Since
![]() $E_0 \cong _K E$
and
$E_0 \cong _K E$
and
![]() $E_0$
has full
$E_0$
has full
![]() $2$
-torsion over K, it follows that E also has full
$2$
-torsion over K, it follows that E also has full
![]() $2$
-torsion over K.
$2$
-torsion over K.
Put E into global minimal Weierstrass form
By completing the square, we may transform to a model for E of the form
where
![]() $f \in \mathcal {O}_K[x]$
is monic of degree
$f \in \mathcal {O}_K[x]$
is monic of degree
![]() $3$
, and this model is a local minimal Weierstrass model at all primes
$3$
, and this model is a local minimal Weierstrass model at all primes
![]() $\mathfrak {q}$
of K coprime to
$\mathfrak {q}$
of K coprime to
![]() $2 \mathcal {O}_K$
.
$2 \mathcal {O}_K$
.
Using (6.5), we deduce that u is an S-unit in
![]() $\mathcal {O}_K$
by definition of local minimal Weierstrass model (i.e., a Weierstrass model over
$\mathcal {O}_K$
by definition of local minimal Weierstrass model (i.e., a Weierstrass model over
![]() $\mathcal {O}_{K_{\mathfrak {q}}}$
whose discriminant has minimal valuation). Furthermore, by
$\mathcal {O}_{K_{\mathfrak {q}}}$
whose discriminant has minimal valuation). Furthermore, by
![]() $E_0 \cong _K E$
and (6.4), there is some permutation of
$E_0 \cong _K E$
and (6.4), there is some permutation of
![]() $e_1, e_2, e_3$
such that
$e_1, e_2, e_3$
such that
 $$ \begin{align*} & u^2 e_1 + \beta = 0, \\[2pt] & u^2 e_2 + \beta = a, \\[2pt] & u^2 e_3 + \beta = -b, \end{align*} $$
$$ \begin{align*} & u^2 e_1 + \beta = 0, \\[2pt] & u^2 e_2 + \beta = a, \\[2pt] & u^2 e_3 + \beta = -b, \end{align*} $$
or equivalently
Conversely, given an elliptic curve E over K of conductor N and full
![]() $2$
-torsion over K, we can produce an obstructive solution
$2$
-torsion over K, we can produce an obstructive solution
![]() $(a,b,c) := (a, b, -a-b)$
if and only if there is an S-unit u of K such that a and b are coprime in (6.9) and (6.10). A triple
$(a,b,c) := (a, b, -a-b)$
if and only if there is an S-unit u of K such that a and b are coprime in (6.9) and (6.10). A triple
![]() $(a,b,c)$
produced from E is unique up to multiplication by the square of a unit in
$(a,b,c)$
produced from E is unique up to multiplication by the square of a unit in
![]() $\mathcal {O}_K$
(and up to a choice of labeling of
$\mathcal {O}_K$
(and up to a choice of labeling of
![]() $e_1, e_2, e_3 \in K$
).
$e_1, e_2, e_3 \in K$
).
We have determined the list of obstructive solutions for both
![]() $\mathbb {Q}(\sqrt {5})$
and
$\mathbb {Q}(\sqrt {5})$
and
![]() $\mathbb {Q}(\sqrt {17})$
, which can be found in the electronic resources for this paper [Reference Chen, Efemwonkieke and Sun3]. For those congruence classes of exponents p where we obtain a result, all obstructive solutions are eliminated by the reciprocity constraints. For those congruence classes of exponents p where we do not obtain a result, there is some obstructive solution that is not eliminated by the reciprocity constraints.
$\mathbb {Q}(\sqrt {17})$
, which can be found in the electronic resources for this paper [Reference Chen, Efemwonkieke and Sun3]. For those congruence classes of exponents p where we obtain a result, all obstructive solutions are eliminated by the reciprocity constraints. For those congruence classes of exponents p where we do not obtain a result, there is some obstructive solution that is not eliminated by the reciprocity constraints.
We end by illustrating the two methods for listing the obstructive solutions
![]() $(a,b,c)$
to (1.1) for
$(a,b,c)$
to (1.1) for
![]() $K = \mathbb {Q}(\sqrt {5})$
. The first method starts with the solutions
$K = \mathbb {Q}(\sqrt {5})$
. The first method starts with the solutions
![]() $(U,V)$
to the S-unit equation (6.2):
$(U,V)$
to the S-unit equation (6.2):
 $$ \begin{align} \left(2, -1\right), \left(\frac{-\sqrt{5}+1}{4}, \frac{\sqrt{5}+3}{4} \right), \left(\frac{-\sqrt{5} -1}{2}, \frac{\sqrt{5}+3}{2} \right), \left(\frac{\sqrt{5}+2}{4}, \frac{-\sqrt{5}+2}{4} \right), \\\left(4\sqrt{5} - 8, -4\sqrt{5} + 9\right), \left( \frac{-\sqrt{5}+1}{2}, \frac{\sqrt{5}+1}{2} \right), \left(-4\sqrt{5} - 8, 4\sqrt{5} + 9\right), \nonumber \\\left( \frac{-\sqrt{5} +3}{2}, \frac{\sqrt{5}-1}{2} \right), \left(-\sqrt{5} - 2, \sqrt{5} + 3\right), \left(-\sqrt{5} - 1, \sqrt{5} + 2\right), \left(\frac{\sqrt{5}+1}{4}, \frac{-\sqrt{5}+3}{4} \right), \nonumber\\\left(-\sqrt{5} + 2, \sqrt{5} - 1\right), \left(-\sqrt{5} + 3, \sqrt{5} - 2\right), \left(\frac{1}{2}, \frac{1}{2}\right), \nonumber \end{align} $$
$$ \begin{align} \left(2, -1\right), \left(\frac{-\sqrt{5}+1}{4}, \frac{\sqrt{5}+3}{4} \right), \left(\frac{-\sqrt{5} -1}{2}, \frac{\sqrt{5}+3}{2} \right), \left(\frac{\sqrt{5}+2}{4}, \frac{-\sqrt{5}+2}{4} \right), \\\left(4\sqrt{5} - 8, -4\sqrt{5} + 9\right), \left( \frac{-\sqrt{5}+1}{2}, \frac{\sqrt{5}+1}{2} \right), \left(-4\sqrt{5} - 8, 4\sqrt{5} + 9\right), \nonumber \\\left( \frac{-\sqrt{5} +3}{2}, \frac{\sqrt{5}-1}{2} \right), \left(-\sqrt{5} - 2, \sqrt{5} + 3\right), \left(-\sqrt{5} - 1, \sqrt{5} + 2\right), \left(\frac{\sqrt{5}+1}{4}, \frac{-\sqrt{5}+3}{4} \right), \nonumber\\\left(-\sqrt{5} + 2, \sqrt{5} - 1\right), \left(-\sqrt{5} + 3, \sqrt{5} - 2\right), \left(\frac{1}{2}, \frac{1}{2}\right), \nonumber \end{align} $$
as computed by SageMath and listed up to permutation of
![]() $U,V$
.
$U,V$
.
For triples
![]() $(a,b,c), (u,v,w) \in K^3$
, we write
$(a,b,c), (u,v,w) \in K^3$
, we write
![]() $(a,b,c) \sim (u,v,w)$
if
$(a,b,c) \sim (u,v,w)$
if
![]() $(a,b,c)$
is a nonzero scalar multiple of a permutation of
$(a,b,c)$
is a nonzero scalar multiple of a permutation of
![]() $(u,v,w)$
. Consider the set
$(u,v,w)$
. Consider the set
 $$ \begin{align*} \mathfrak{S} &= \left\{ (a,b,c) \in \mathcal{O}_K^3 : (a,b,c) \sim (U, V, -1), (U,V) \text{ is an }S\text{-unit solution,}\right.\\ & \qquad \left. \text{and } (a, b, c) \text{ is primitive} \right\}\hspace{-1pt}. \end{align*} $$
$$ \begin{align*} \mathfrak{S} &= \left\{ (a,b,c) \in \mathcal{O}_K^3 : (a,b,c) \sim (U, V, -1), (U,V) \text{ is an }S\text{-unit solution,}\right.\\ & \qquad \left. \text{and } (a, b, c) \text{ is primitive} \right\}\hspace{-1pt}. \end{align*} $$
The obstructive solutions to (1.1) are the triples
![]() $(a,b,c) \in \mathfrak {S}$
such that the conductor of
$(a,b,c) \in \mathfrak {S}$
such that the conductor of
![]() $E_{a,b,c}$
is
$E_{a,b,c}$
is
![]() $8 \mathcal {O}_K$
. As we consider obstructive solutions up to equivalence by multiplication by the square of a unit in
$8 \mathcal {O}_K$
. As we consider obstructive solutions up to equivalence by multiplication by the square of a unit in
![]() $\mathcal {O}_K$
, the set
$\mathcal {O}_K$
, the set
![]() $\mathfrak {S}$
is finite up to this equivalence and representatives can be computed from (11).
$\mathfrak {S}$
is finite up to this equivalence and representatives can be computed from (11).
In the second method, we consider each of the elliptic curves E over K with conductor
![]() $8 \mathcal {O}_K$
and produce if possible an obstructive solution
$8 \mathcal {O}_K$
and produce if possible an obstructive solution
![]() $(a,b,c)$
from it using the process described in the previous paragraphs.
$(a,b,c)$
from it using the process described in the previous paragraphs.
Both methods give the same list up to equivalence by multiplication by the square of a unit in
![]() $\mathcal {O}_K$
. In all, there are
$\mathcal {O}_K$
. In all, there are
![]() $12$
obstructive solutions to (1.1) over
$12$
obstructive solutions to (1.1) over
![]() $K = \mathbb {Q}(\sqrt {5})$
, up to equivalence by multiplication by the square of a unit in
$K = \mathbb {Q}(\sqrt {5})$
, up to equivalence by multiplication by the square of a unit in
![]() $\mathcal {O}_K$
:
$\mathcal {O}_K$
:
 $$ \begin{align} \left(-1, -4\sqrt{5} - 8, 4\sqrt{5} + 9\right), \left(4\sqrt{5} + 8, 1, -4\sqrt{5} - 9\right), \\\left(-1, \frac{\sqrt{5} + 3}{2}, \frac{-\sqrt{5} - 1}{2} \right), \left(1, \frac{-\sqrt{5} + 1}{2}, \frac{\sqrt{5} - 3}{2}\right), \nonumber\\\left( \frac{-3\sqrt{5} - 7}{2}, 2\sqrt{5} + 2, \frac{-\sqrt{5} + 3}{2} \right), \left( \frac{-\sqrt{5} - 1}{2}, -1, \frac{\sqrt{5} + 3}{2}\right), \nonumber\\\left( \frac{\sqrt{5} + 1}{2}, \frac{-\sqrt{5} - 3}{2}, 1 \right), \left( 4\sqrt{5} + 9, -1, -4\sqrt{5} - 8\right), \nonumber\\\left(-4\sqrt{5} + 8, 1, 4\sqrt{5} - 9\right), \left(1, -4\sqrt{5} - 9, 4\sqrt{5} + 8\right), \nonumber\\\left( \frac{-\sqrt{5} + 3}{2}, \frac{\sqrt{5} - 1}{2}, -1\right), \left( \frac{-\sqrt{5} - 3}{2}, 1, \frac{\sqrt{5} + 1}{2}\right). \nonumber \end{align} $$
$$ \begin{align} \left(-1, -4\sqrt{5} - 8, 4\sqrt{5} + 9\right), \left(4\sqrt{5} + 8, 1, -4\sqrt{5} - 9\right), \\\left(-1, \frac{\sqrt{5} + 3}{2}, \frac{-\sqrt{5} - 1}{2} \right), \left(1, \frac{-\sqrt{5} + 1}{2}, \frac{\sqrt{5} - 3}{2}\right), \nonumber\\\left( \frac{-3\sqrt{5} - 7}{2}, 2\sqrt{5} + 2, \frac{-\sqrt{5} + 3}{2} \right), \left( \frac{-\sqrt{5} - 1}{2}, -1, \frac{\sqrt{5} + 3}{2}\right), \nonumber\\\left( \frac{\sqrt{5} + 1}{2}, \frac{-\sqrt{5} - 3}{2}, 1 \right), \left( 4\sqrt{5} + 9, -1, -4\sqrt{5} - 8\right), \nonumber\\\left(-4\sqrt{5} + 8, 1, 4\sqrt{5} - 9\right), \left(1, -4\sqrt{5} - 9, 4\sqrt{5} + 8\right), \nonumber\\\left( \frac{-\sqrt{5} + 3}{2}, \frac{\sqrt{5} - 1}{2}, -1\right), \left( \frac{-\sqrt{5} - 3}{2}, 1, \frac{\sqrt{5} + 1}{2}\right). \nonumber \end{align} $$
Acknowledgment
We would like to thank Alain Kraus for helpful comments and improvements on an earlier version of this paper, and Nuno Freitas and Samir Siksek for useful comments about the problems studied in this paper.