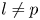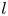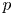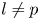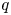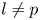Generic local deformation rings when $l \neq p$

Abstract

We determine the local deformation rings of sufficiently generic mod $l$ representations of the Galois group of a $p$-adic field, when $l \neq p$, relating them to the space of $q$-power-stable semisimple conjugacy classes in the dual group. As a consequence, we give a local proof of the $l \neq p$ Breuil–Mézard conjecture of the author, in the tame case.

1. Introduction

We study the moduli space $\mathfrak {X}$ of $n$-dimensional $l$-adic representations of the tame Weil group of a $p$-adic field $F$, when $l \neq p$ are primes and $n \geqslant 1$ is an integer. The main geometric result, Theorem 2.16, is a simple description of the completion of $\mathfrak {X}$ at a sufficiently general point of its special fibre. We then apply this to give a purely local proof of the author's $l \neq p$ analogue of the Breuil–Mézard conjecture in the tame case (see Theorem 4.2). This was formulated, and proved for $l \geqslant 3$ by global automorphic methods, in [Sho18]. This result links congruences between representations of ${\rm GL}_n(k)$, where $k$ is the residue field of $F$, and ‘congruences’ between irreducible components of $\mathfrak {X}$; for more background and motivation, see the introduction to [Sho18].

We give a more precise description of our results and methods in the most critical case. Let $W_t$ be the tame Weil group and $I_t$ be the tame inertia group of $F$, and let $(\mathcal {O}, E, \mathbb {F})$ be a sufficiently large $l$-adic coefficient system. Let $q$ be the order of $k$, the residue field of $F$, and let $\sigma$ be a choice of topological generator of $I_t$. Suppose that $\overline {\rho } : W_t \rightarrow {\rm GL}_n(\mathbb {F})$ is a representation such that $\overline {\rho }(\sigma )$ is regular unipotent.

Let $\hat {T}$ be a maximal split torus in ${\rm GL}_{n, \mathcal {O}}$ and let $W$ be the Weyl group. We have a ‘characteristic polynomial’ map

\[ \mathrm{ch} : {\rm GL}_{n, \mathcal{O}} \rightarrow \hat{T}/W. \]

We consider the $q$-fixed subscheme of $\hat {T}/W$, which we denote by

\[ (\hat{T}/W)^{q}, \]

and its localization at the point $\overline {e}$ of its special fibre corresponding to the identity in $\hat {T}(\mathbb {F})$.

Theorem A (Theorem 2.23)

The morphism

\[ \mathfrak{X}^{\wedge}_{\overline{\rho}} \rightarrow (\hat{T}/W)^{q}_{\overline{e}} \]

defined by $\rho \mapsto \mathrm {ch}(\rho (\sigma ))$ is formally smooth, where $\mathfrak {X}^{\wedge }_{\overline {\rho }}$ is the completion of $\mathfrak {X}$ at the point corresponding to $\overline {\rho }$.

Note that the completion $\mathfrak {X}^{\wedge }_{\overline {\rho }}$ is simply the framed deformation ring of $\overline {\rho }$. The proof of Theorem A is an elaboration of the proof of Proposition 7.10 in [Sho18].

More generally, to each irreducible component $\mathcal {C}$ of the special fibre of $\mathfrak {X}$ we associate a Levi subgroup $\hat {M} \subset {\rm GL}_{n, \mathcal {O}}$ containing $\hat {T}$, with Weyl group $W_{\hat {M}} \subset W$, and an $\mathbb {F}$-point $\overline {s}$ of $(\hat {T}/W_{\hat {M}})^{q}$. Roughly, $\hat {M}$ is minimal such that there is $\overline {\rho }$ on $\mathcal {C}$, and on no other component, such that $\overline {\rho }$ factors through a map to $\hat {M}$ and $\overline {\rho }(\sigma )$ is regular in $\hat {M}$. By choosing $\overline {\rho }$ carefully we can make sure that all its deformations can be conjugated (canonically) to land in $\hat {M}$. Thus for sufficiently general points $\overline {\rho }$ on $\mathcal {C}$ we obtain a morphism

\[ \text{``}\mathrm{ch}_{\hat{M}}(\rho(\sigma))\text{''} : \mathfrak{X}^{\wedge}_{\overline{\rho}} \rightarrow (\hat{T}/W_{\hat{M}})^{q}_{\overline{s}} \]

and show that it is formally smooth (see Theorem 2.16). The proof proceeds by reducing first to the case that $\overline {\rho }(g)$ is unipotent for all $g\in I_t$ (see § 2.9), and then to the situation of Theorem A (see Corollary 2.22).

We explain the application to the $l \neq p$ ‘Breuil–Mézard conjecture’ of [Sho18] in the tame case, whose statement we briefly recall. Set $G = {\rm GL}_{n, k}$. Let $\mathcal {Z}(\mathfrak {X})$ (respectively, $\mathcal {Z}(\mathfrak {X}_\mathbb {F})$) be the free abelian group on the irreducible components of $\mathfrak {X}$ (respectively, $\mathfrak {X}_{\mathbb {F}}$). Let $K_E(G(k))$ (respectively, $K_\mathbb {F}(G(k))$) be the Grothendieck groups of representations of $G(k)$ over $E$ (respectively, $\mathbb {F}$). There is a ‘cycle map’

\[ \operatorname{cyc} : K_E(G(k)) \rightarrow \mathcal{Z}(\mathfrak{X}) \]

motivated by the local Langlands correspondence (see § 4), and natural ‘reduction maps’ $\operatorname {red} : K_E(G(k)) \rightarrow K_\mathbb {F}(G(k))$ and $\operatorname {red} : \mathcal {Z}(\mathfrak {X}) \rightarrow \mathcal {Z}(\mathfrak {X}_{\mathbb {F}})$. We then have the following result.

Theorem B (Theorem 4.2)

There is a unique map $\overline {\operatorname {cyc}} : K_\mathbb {F}(G(k)) \rightarrow \mathcal {Z}(\mathfrak {X}_\mathbb {F})$ such that the diagram

commutes.

If $l > 2$ then Theorem B follows from the main theorem of [Sho18], but we provide a purely local proof here (in the tame case). If $l = 2$ then Theorem B is new.

It is enough to prove Theorem B after formally completing at some $\overline {\rho }$ on each component. We explain how to do this for $\overline {\rho }$ as in Theorem A. Let $\Gamma$ be the (integral) Gelfand–Graev representation of $G(k)$ over $\mathcal {O}$; it is a projective $\mathcal {O}[G(k)]$ representation. Let $B_{q,n}$ be the coordinate ring of $(\hat {T}/W)^{q}$. Via the ‘Curtis homomorphisms’ we define a homomorphism

(1)\begin{equation} B_{q,n} \rightarrow \operatorname{End}(\Gamma)\otimes E\end{equation}

which restricts to a homomorphism

\[ B_{q,n,\overline{e}} \rightarrow \operatorname{End}(e\Gamma)\otimes E \]

for a certain idempotent $e \in \mathcal {O}[G(k)]$. (For this, we need a result of Broué and Michel in [BM89] on the blocks of $\mathcal {O}$-representations of $G(k)$). The special fibre of $\mathfrak {X}_{\overline {\rho }}^{\wedge }$ has a unique irreducible component $\mathcal {C}$, and we may define

\[ \overline{\operatorname{cyc}}(\sigma) = \dim_{\mathbb{F}} \operatorname{Hom}(\Gamma, \sigma)[\mathcal{C}]. \]

That this works is essentially a consequence of the projectivity of $\Gamma$, together with Theorem A.

The proof of Theorem B is carried out in §§ 3 and 4: in § 3 we recall the necessary material on Gelfand–Graev and Deligne–Lusztig representations, and this is applied to Theorem B in § 4.

The functor $\operatorname {Hom}(\Gamma, \cdot )$ plays the role in this proof that the functor $M_\infty (\cdot )$ plays in the global proof via patching, and so one could see the relationship between this paper and [Sho18] as being parallel to that between [Paš15] and [Kis09].

Helm and Moss have proved in [Hel20, HM18] that the local Langlands correspondence in families, conjectured in [EH14], exists. As a consequence, or byproduct, of their proof, it follows that the map (1) actually defines an isomorphism

(2)\begin{equation} B_{q,n} \xrightarrow{\sim} \operatorname{End}(\Gamma).\end{equation}

This is a result purely in the representation theory of finite groups, and it would be interesting to have an elementary proof. For $l > n$, one has been given by Li in [Li21]; we return to this below. Results on the endomorphism rings of integral Gelfand–Graev representations (for general reductive groups) were obtained by Bonnafé and Kessar in [BK08], under the assumption that $l$ does not divide the order of the Weyl group (and is distinct from $p$). Their description of the endomorphism ring is quite different, not involving $(\hat {T}/W)^{q}$, and can genuinely fail if $l \mid |W|$.

The idea of using the Gelfand–Graev representations came from [Hel20]. Having proved Theorem A, I asked David Helm whether the map (2) could be an isomorphism and our correspondence turned up an error in an earlier version of [Hel20], which was corrected by him using, among other things, the map (2) and the idea behind the proof of Theorem A. He was then able to show that the map (2) was indeed an isomorphism, as a consequence of his work with Moss. There are other ways to deduce Theorem B from Theorem A; my original method was a complicated combinatorial induction.

We take some care to write things in a way that is independent of a choice of topological generator of $I_t$. Thus instead of $(\hat {T}/W)^{q}$ we actually use the space of $q$-stable $W$-orbits of homomorphisms $I_t \rightarrow \hat {T}$. Points of this space over $E$ then canonically parametrize Deligne–Lusztig representations of ${\rm GL}_n(k)$ over $E$, a construction we learned from [DR09].

1.1 Generalizations

It is clear that much of § 3 would go through for a general reductive group. Since the writing of the first version of this paper, Li [Li21] has done this and, much more, has given a local proof of the isomorphism (2) for $G$ a connected reductive group over $\mathbb {F}_q$ with connected centre, again under the assumption that $l$ does not divide the order of the Weyl group. Remarkably, his proof uses the mod $p$ representation theory of $G(\mathbb {F}_q)$, despite the fact that the theorem is a result in the mod $l$ representation theory.

Extending the geometric results of § 2 to the case of general groups seems to be more difficult. In forthcoming work, we hope to partially generalize the main geometric result, Theorem 2.16, to this setting. However, this will not cover points on every irreducible component of the moduli space of tame parameters, and will therefore not be enough for a Breuil–Mézard-type conjecture.

In another direction, one could hope to remove the restrictions to tamely ramified parameters and to representations of ${\rm GL}_n(\mathcal {O}_F)$ with $K(1)$-fixed vectors. The geometric results should generalize straightforwardly to the full moduli space of Langlands parameters. It seems likely that this could be combined with Bushnell–Kutzko-type theory to prove the $l\neq p$ Breuil–Mézard conjecture in the form that only involves Schneider–Zink types (see [Sho18, Remark 4.7]). It is not clear how to extend this to all representations of ${\rm GL}_n(\mathcal {O}_F)$, even when only considering the moduli space of tame parameters as in the present paper. See Remark 4.3 for further discussion of this point.

1.2 Notation

An $l$-adic coefficient system is a triple $(E, \mathcal {O}, \mathbb {F})$ where $E$ is a finite extension of $\mathbb {Q}_l$, $\mathcal {O}$ is its ring of integers, and $\mathbb {F}$ is its residue field. We then define $\mathcal {C}_{\mathcal {O}}$ to be the category of Artinian local $\mathcal {O}$-algebras with residue field $\mathbb {F}$, and $\mathcal {C}^{\wedge }_{\mathcal {O}}$ be the category of complete Artinian local $\mathcal {O}$-algebras that are inverse limits of objects of $\mathcal {C}_{\mathcal {O}}$. We also consider affine formal schemes of the form $\operatorname {Spf}(R)$ for $R$ an object of $\mathcal {C}_{\mathcal {O}}$ or $\mathcal {C}_{\mathcal {O}}^{\wedge }$ (taken with respect to the $\mathfrak {m}_R$-adic topology); these form categories which we denote by $\mathcal {FS}_{\mathcal {O}}$ or $\mathcal {FS}_{\mathcal {O}}^{\wedge }$, respectively (and which are canonically isomorphic to the opposite categories of $\mathcal {C}_{\mathcal {O}}$ and $\mathcal {C}_{\mathcal {O}}^{\wedge }$). For $X \in \mathcal {FS}_{\mathcal {O}}^{\wedge }$ and $A \in \mathcal {C}_{\mathcal {O}}^{\wedge }$ we write $X(A) = \operatorname {Hom}_{\mathcal {FS}_{\mathcal {O}}^{\wedge }}(\operatorname {Spf}(A),X)$. If $X/\mathcal {O}$ is a scheme locally of finite type, and $x \in X(\mathbb {F})$, then we let $X^{\wedge }_x = \operatorname {Spf}\big (\varprojlim \mathcal {O}_{X, x}/\mathfrak {m}_{X,x}^{n}\big )$ be its formal completion, an object of $\mathcal {FS}_{\mathcal {O}}^{\wedge }$.

If $A$ is a ring, we write $\operatorname {diag}(x_1, \ldots, x_n)$ for the diagonal matrix with entries $x_1, \ldots, x_n$. If $\zeta \in A$ and $n\in \mathbb {N}$, then we write $J_n(\zeta )$ for the $n \times n$ Jordan block matrix with $\zeta$ on the diagonal and $1$ on the superdiagonal.

2. Moduli of Weil group representations

2.1 Galois groups

Choose a maximal tamely ramified extension $F^{t}$ of $F$. This induces an algebraic closure $\overline {k}$ of $k$. For $n \in \mathbb {N}$, let $k_n$ be the subextension of $\overline {k}/k$ having degree $n$ over $k$. Let $G_t = \operatorname {Gal}(F^{t}/F)$. The canonical homomorphism $G_t \rightarrow G_k = \operatorname {Gal}(\overline {k}/k) \cong \hat {\mathbb {Z}}$ has kernel the tame inertia subgroup $I_t$, and the tame Weil group $W_t \subset G_t$ is the preimage of $\mathbb {Z}$ under this homomorphism.

There is a canonical isomorphism

\[ I_t \xrightarrow{\sim} \varprojlim k_n^{\times} \]

where the inverse limit is under the norm maps $k_n \rightarrow k_m$ for $m \mid n$. The exact sequence

\[ 1 \rightarrow I_t \rightarrow G_t \rightarrow G_k \rightarrow 1 \]

splits, so that we have a canonical isomorphism

\[ G_t \cong (\varprojlim k_n^{\times}) \rtimes G_k \]

where $G_k$ acts on each $k_n^{\times }$ in the natural way. More concretely, if we choose a topological generator $\sigma \in I_t$ and lift $\phi \in G_t$ of arithmetic Frobenius, then $G_t$ is isomorphic to the profinite completion of

\[ \big\langle \phi, \sigma | \phi \sigma \phi^{-1} = \sigma^{q}\big\rangle. \]

Note that, as a topological group, this only depends on the integer $q$. A pair $(\sigma, \phi )$ as above will be called (a choice of) standard (topological) generators of $G_t$ (or $W_t$).

2.2 Moduli spaces

Fix an $l$-adic coefficient system $(E, \mathcal {O}, \mathbb {F})$. Let $\hat {G}$ be an algebraic group over $\mathcal {O}$ isomorphic to a product of finitely many general linear groups (for the proofs of all the statements below, we can and do immediately reduce to the case of ${\rm GL}_n/\mathcal {O}$, but the slight extra generality will be useful later). We assume throughout that $E$ is sufficiently large in the following sense: if $n$ is the rank of $\hat {G}$, then

(3)\begin{equation} \text{$E$ contains the $(q^{n!}-1)$th roots of unity.} \end{equation}

This avoids rationality issues; we have not tried to optimize this assumption.

Proposition 2.1 The functor taking an $\mathcal {O}$-algebra $A$ to the set of continuous¹ homomorphisms

\[ \rho : W_t \rightarrow \hat{G}(A) \]

is representable by an affine scheme $\mathfrak {X}^{\hat {G}}(q)$ of finite type over $\mathcal {O}$ that is reduced, $\mathcal {O}$-flat, and a local complete intersection of dimension $\dim _\mathcal {O}({\hat {G}}) + 1$.

Remark 2.2 Work of Dat, Helm, Kurinczuk and Moss [DHKM20] shows that the analogous result holds with $\hat {G}$ replaced by an arbitrary split connected reductive group over $\mathbb {Z}_l$. In fact, their result is more general than this: on the one hand, there is no restriction to the tame Weil group, and on the other, $\hat {G}$ may be replaced with the $L$-group of any connected reductive group over $F$.

Proof. We may and do assume that $\hat {G} = {\rm GL}_n/\mathcal {O}$ for some $n$. Choose standard topological generators $\sigma$ and $\phi$ of $W_t$, and let $W'_t$ be the subgroup they generate. As $W'_t$ is finitely generated, it is clear that the functor taking $A$ to the set of homomorphisms $\rho : W'_t \rightarrow \hat {G}(A)$ is representable by a finite-type affine scheme $\mathfrak {X}$ over $\mathbb {Z}_l$. Moreover, [Hel20, Proposition 6.2] implies that $\mathfrak {X}$ enjoys the geometric properties that we are claiming for $\mathfrak {X}^{\hat {G}}(q)$.

Lemma 2.3 Suppose that $A$ is a $\mathbb {Z}_l$-algebra and that $M$ is a finite $A$-module, free of rank $n$, with an $A$-linear action $\rho$ of $W'_t$. Then there is a unique continuous $A$-linear action $\tilde {\rho }$ of $W_t$ on $M$ extending that of $W'_t$.

Proof. First note that every finite image representation of $W'_t$ extends uniquely to a continuous representation of $W_t$ (and even of $G_t$, since $G_t$ is the profinite completion of $W'_t$).

Let $A$, $M$ and $\rho$ be as in the lemma. I claim that $(\sigma ^{q^{n!} - 1} - 1)^{n}$ acts as zero on $M$. Indeed, it suffices to check that this holds for the universal representation of $W'_t$ over $\mathfrak {X}$. This in turn can be checked at geometric points in characteristic zero, since $\mathfrak {X}$ is of finite type, $\mathbb {Z}_l$-flat and reduced. But at such points the eigenvalues of $\sigma$ are permuted by the $q$-power map, and so fixed by the $q^{n!}$-power map. Thus they are all $(q^{n!}-1)$th roots of unity. The result follows from the Cayley–Hamilton theorem.

It follows that the $\mathbb {Z}_l$-subalgebra $\mathcal {E}$ of $\operatorname {End}_A(M)$ generated by $\rho (\sigma )$ is a finitely generated $\mathbb {Z}_l$-module. Thus there is a finitely generated $\mathbb {Z}_l$-submodule $N$ of $M$ that generates $M$ as an $A$-module and that is preserved by $\sigma$, so that $\mathcal {E} \subset \operatorname {End}(N)$. I claim that the map $k \mapsto \rho (\sigma )^{k}$ is a continuous map from $\mathbb {Z}$, equipped with the linear topology whose open ideals are $m\mathbb {Z}$ for $m$ coprime to $p$, to $\operatorname {End}(N)$. If $k \equiv k' \mod q^{n!} - 1$, then by the previous paragraph ${(\rho (\sigma )^{k - k'} - 1)^{n} = 0}$. It follows that, for every $s \in \mathbb {N}$, there exists $r \in \mathbb {N}$ such that $\rho (\sigma )^{k - k'} \equiv 1$ in $\operatorname {End}(N/l^{s}N)$ for all $k \equiv k' \mod (q^{n!} - 1)l^{r}$. This is the required continuity. We deduce that $\rho$ extends to a unique continuous map from the completion of $\langle \sigma \rangle$ with respect to this topology to $\mathcal {E} \subset \operatorname {End}(N)$. This completion is canonically isomorphic to $I_t$, and we therefore obtain a continuous homomorphism $I_t \rightarrow \mathcal {E} \subset \operatorname {End}(M)$. It follows from the unicity that this extends to a continuous homomorphism $W'_t \rightarrow \operatorname {End}(M)$.

Proposition 2.1 follows immediately, with $\mathfrak {X}^{\hat {G}}(q) = \mathfrak {X}$.

Remark 2.4 The reason for formulating Proposition 2.1 with $W_t$ rather than the subgroup $W'_t$ used in the proof is to get a moduli space whose definition does not require a choice of $\sigma$.

2.3 Parameters

Let $C$ be a field containing $\mathbb {F}$ or $E$, and let ${\hat {G}}$ be as above. In what follows, we will usually omit the word ‘tame’, since that is the only case we consider in this paper.

Definition 2.5 A (tame) ${\hat {G}}$-parameter over $C$ is a $\hat {G}(C)$-conjugacy class of homomorphisms $\rho : W_t \rightarrow {\hat {G}}(C)$.

A homomorphism $\tau : I_t \rightarrow {\hat {G}}(C)$ is extendable if it extends to a homomorphism $W_t \rightarrow \hat {G}(C)$; equivalently, if $\tau$ is conjugate in $\hat {G}(C)$ to the homomorphism $\tau ^{q}$. It is semisimple/unipotent if every element of its image is.

A (tame) inertial ${\hat {G}}$-parameter over $C$ is a ${\hat {G}}(C)$-conjugacy class of extendable homomorphisms $\tau : I_t \rightarrow {\hat {G}}(C)$. It is semisimple/unipotent if every homomorphism in its conjugacy class is. Since $I_t$ is pro-cyclic, any inertial ${\hat {G}}$-parameter has a unique Jordan decomposition $\tau = \tau _s \tau _u$ where $\tau _s$ is a semisimple inertial $\hat {G}$-parameter, $\tau _u$ is a unipotent inertial $\hat {G}$-parameter, and the images of $\tau _s$ and $\tau _u$ commute.

For every inertial ${\hat {G}}$-parameter $\tau$ over $C$, let $\mathfrak {X}^{\hat {G}}(q, \tau )$ be the Zariski closure of the $\overline {C}$-points $\rho$ of $\mathfrak {X}^{\hat {G}}(q)$ such that $\rho |_{I_t} \sim \tau$. Then as in [Sho18, Proposition 2.6], we have the following proposition.

Proposition 2.6 The assignment $\tau \mapsto \mathfrak {X}^{\hat {G}}(q,\tau )$ is a bijection between semisimple inertial ${\hat {G}}$-parameters over $C$ and irreducible components of $\mathfrak {X}^{\hat {G}}(q)_C$.

2.4 Moduli of semisimple parameters

Let ${\hat {T}}$ be a maximal split torus in ${\hat {G}}$, and let $W$ be its Weyl group. Then the quotient ${\hat {T}}/W$ is a smooth affine scheme over $\mathcal {O}$ of relative dimension the rank of ${\hat {G}}$. If ${\hat {G}} = {\rm GL}_n$ and ${\hat {T}}$ is the standard torus, then we write an element of ${\hat {T}}$ as $\operatorname {diag}(x_1, \ldots, x_n)$. Then ${\hat {T}} = \operatorname {Spec}\mathcal {O}[x_1^{\pm 1}, \ldots, x_n^{\pm 1}]$ and

\[ {\hat{T}}/W = \operatorname{Spec} \mathcal{O}[x_1^{\pm 1}, \ldots, x_n^{\pm 1}]^{S_n} = \operatorname{Spec} \mathcal{O}[e_1, \ldots, e_n, e_n^{\pm 1}] \]

where $e_i$ is the $i$th elementary symmetric polynomial in the $x_i$.

Lemma 2.7 There is a unique $\mathcal {O}$-morphism $\mathrm {ch} : {\hat {G}} \rightarrow {\hat {T}}/W$ that extends the quotient map ${\hat {T}} \rightarrow {\hat {T}}/W$ and is invariant under conjugation.

Proof. We can reduce to the case when ${\hat {G}} = {\rm GL}_n$ and ${\hat {T}}$ is the standard torus. Then the map takes $g$ to the point of ${\hat {T}}/W$ at which $e_i$ is the $X^{i}$-coefficient in the characteristic polynomial of $g$.

Definition 2.8 The $q$-power morphism $q : {\hat {T}} \rightarrow {\hat {T}}$ takes $t$ to $t^{q}$. It descends to a morphism

\[ q : {\hat{T}}/W \rightarrow {\hat{T}}/W. \]

We write $({\hat {T}}/W)^{q}$ for the fixed-point scheme of $q : {\hat {T}}/W \rightarrow {\hat {T}}/W$.

If ${\hat {G}} = {\rm GL}_n$ and ${\hat {T}}$ is standard, we write $q^{*}e_i$ for the polynomial in the $x_i$ such that $q^{*}e_i(x_1, \ldots, x_n) = e_i(x_1^{q}, \ldots, x_n^{q})$, and let

\[ I_{q,n} \lhd \mathcal{O}[e_1, \ldots, e_n, e_n^{-1}] \]

be the ideal generated by $(q^{*}e_i - e_i)_{i=1}^{n}$. Then

\[ ({\hat{T}}/W)^{q} = \operatorname{Spec} B_{q,n} \]

for $B_{q,n} = \mathcal {O}[e_1, \ldots, e_n, e_n^{-1}]/I_{q,n}$.

Lemma 2.9 The fixed-point scheme $({\hat {T}}/W)^{q}$ is finite flat over $\operatorname {Spec} \mathcal {O}$ and reduced.

Proof. Again, we assume that ${\hat {G}} = {\rm GL}_n$ and ${\hat {T}}$ is the standard torus. I claim that $B_{q,n} = \mathcal {O}[e_1, \ldots, e_n, e_n^{-1}]/I_q$ is generated as an $\mathcal {O}$-module by monomials of the form $e_1^{a_1}e_2^{a_2}\ldots e_n^{a_n}$ where $0 \leqslant a_i \leqslant q - 1$ for all $i$, and $a_n < q-1$. Granted this, we see that $B_{q,n}$ is a finitely generated $\mathcal {O}$-module and that

\[ \dim_{\overline{E}} B_{q,n} \otimes_\mathcal{O} \overline{E} \leqslant q^{n-1}(q-1). \]

However, the number of $E$-points of $B_{q,n}$ is the number of tuples $(z_1, \ldots, z_n)$ of elements of $\overline {E}^{\times }$ that are permuted by the $q$-power map. This number is the same if $\overline {E}^{\times }$ is replaced by $\overline {k}^{\times }$; but then it is simply the number of semisimple conjugacy classes of ${\rm GL}_n(k)$, which is seen to be $q^{n-1}(q-1)$ by considering the characteristic polynomial. This shows that the number of $\overline {E}$-points of $B_{q,n}$ is equal to $\dim _{\overline {E}} B_{q,n}\otimes \overline {E}$ which is in turn equal to the minimal number of generators of $B_{q,n}$ as an $\mathcal {O}$-module, whence the result.

To prove the claim, we make an elementary argument with symmetric functions. If $\lambda = (\lambda _1, \lambda _2, \ldots )$ is a partition of a nonnegative integer $|\lambda |$ in which each positive integer $j$ appears $a_j = a_j(\lambda )$ times, we let $e_\lambda = \prod _{i=1}^{\infty } e_{\lambda _i} = \prod _{j=1}^{\infty } e_j^{a_j}$ (setting $e_j = 0$ for $j > n$, and $0^{0} = 1$). Let $m_\lambda$ be the homogeneous symmetric polynomial in the $x_i$ of type $\lambda$ (that is, the sum of all monomials of the form $\prod _{i=1}^{n} x_{\pi (i)}^{\lambda _i}$ for $\pi \in S_n$), regarded as an element of the ring $\mathcal {O}[e_1, \ldots, e_n]$. Let $M$ be the $\mathcal {O}$-submodule of $\mathcal {O}[e_1, \ldots, e_n]$ spanned by the set

\[ S = \{e_\lambda : a_j(\lambda) \leqslant q \text{ for all } 1 \leqslant i \leqslant n\} \]

and the ideal $I_q$. Suppose that $M \neq \mathcal {O}[e_1, \ldots, e_n]$. Then we may choose $e_\lambda \not \in M$ such that $|\lambda |$ is minimal and such that, subject to this, $\lambda$ is maximal with respect to the dominance order $\succ$ on partitions. By assumption, there is some $j$ such that $a_j(\lambda ) \geqslant q$. Let $\lambda ^{*}$ be the partition such that $e_{\lambda ^{*}}e_j^{q} = e_\lambda$.

Now, we have

\[ m_{(q^{i})} = q^{*}e_i \equiv e_i \mod I_q. \]

By [Sta99, Theorem 7.4.4], $m_{(q^{i})} = e_{(i^{q})} + \sum _{\mu \succ (i^{q})} c_\mu e_\mu$ for some coefficients $c_\mu \in \mathbb {Z}$. Therefore

\[ e_i^{q} = e_{(i^{q})} \equiv e_i - \sum_{\mu \succ (i^{q})} c_\mu e_\mu \mod I_q \]

and so

\[ e_\lambda \equiv e_i e_{\lambda^{*}} - \sum_{\mu \succ (i^{q})}c_\mu e_\mu e_{\lambda^{*}} \mod I_q. \]

As $q \geqslant 2$, $e_i e_{\lambda ^{*}} \in M$ by minimality of $|\lambda |$. Each term $e_{\mu } e_{\lambda ^{*}}$ has the form $e_{\kappa }$ for a partition $\kappa \succ \lambda$ (depending on $\mu$), and is therefore in $M$ by maximality of $\lambda$. Therefore $e_\lambda \in M$, a contradiction.

Thus $\mathcal {O}[e_1, \ldots, e_n]/I_q$ is spanned by those $e_\lambda$ with all $a_j(\lambda ) < q$. In $\mathcal {O}[e_1, \ldots, e_n, e_n^{-1}]/I_q$ we may replace $q^{*}e_n - e_n = e_n^{q} - e_n$ in $I_q$ by $e_n^{q-1} - 1$. It follows that $\mathcal {O}[e_1, \ldots, e_n]/I_q$ is spanned by those $e_\lambda$ with all $a_j(\lambda ) < q$ and with $a_n(\lambda ) < q-1$, as required.

Remark 2.10 We do not actually need this result, and in fact it follows from Theorem 2.16 below and the corresponding facts for $\mathfrak {X}^{\hat {G}}$.

Let $\mathcal {T}$ be the functor taking an $\mathcal {O}$-algebra $A$ to the set of continuous homomorphisms $s : I_t \to \hat {T}(A)$ such that $s(\sigma ^{q^{n!}}) = s(\sigma )$ (where $n$ is the rank of $G$). By the same argument as in the proof of Proposition 2.1, this functor is representable by an affine scheme, $\mathcal {T}$. We define

\[ \mathcal{S}^{\hat{G}}(q) = (\mathcal{T}/W)^{q}. \]

Choosing a generator of $I_t$ shows that $\mathcal {S}^{\hat {G}}(q)$ is isomorphic to $({\hat {T}}/W)^{q}$ (the isomorphism depending on the choice of generator). Recalling that $C$ is a field containing $\mathbb {F}$ or $E$, the $C$-points of $\mathcal {S}^{\hat {G}}(q)$ are in canonical bijection with the semisimple inertial ${\hat {G}}$-parameters over $C$. Restriction to inertia gives a morphism

\[ \mathrm{ch}_{I} : \mathfrak{X}^{\hat{G}}(q) \rightarrow \mathcal{S}^{\hat{G}}(q). \]

2.5 Discrete parameters

Definition 2.11 Let $\tau : I_t \rightarrow {\hat {G}}(C)$ be an extendable homomorphism. We say that $\tau$ is discrete if there is no proper Levi subgroup ${\hat {M}} \subset {\hat {G}}$ such that $\tau$ factors through an extendable homomorphism to $\hat {M}(C)$. We say that an inertial $\hat {G}$-parameter is discrete if every homomorphism in its conjugacy class is.

Lemma 2.12 If $\tau$ is a representative of an inertial ${\hat {G}}$-parameter, then there is a Levi subgroup ${\hat {M}}_\tau$ such that $\tau$ factors through a discrete inertial ${\hat {M}}_\tau$-parameter $\tau : I_t \rightarrow {\hat {M}}_\tau (C)$.

Proof. Indeed, simply take $\hat {M}_\tau$ to be a Levi subgroup that is minimal subject to the condition that $\hat {M}_\tau (C)$ contains $\tau (I_t)$ and that $\tau : I_t \rightarrow \hat {M}(C)$ is extendable.

Concretely, if $[\zeta ] = \{\zeta, \zeta ^{q}, \ldots, \zeta ^{q^{r-1}}\}$ is a $q$-power orbit of prime-to-$p$ order roots of unity in $C$ and $m \geqslant 1$ is an integer, let

\[ J_m([\zeta]) = \bigoplus_{i=1}^{m} J_m(\zeta^{q^{i}}) \]

(recall from § 1.2 that $J_m(\zeta ^{q^{i}})$ denotes a Jordan matrix). Fix a topological generator $\sigma \in I_t$. Then there is some $k \geqslant 1$ and, for $1 \leqslant i \leqslant k$, prime-to-$q$ roots of unity $\zeta _i \in C$ and integers $m_i$, such that $\tau (\sigma )$ is conjugate to

\[ \bigoplus_{i=1}^{k} J_{m_i}([\zeta_i]). \]

We may then take $\hat {M}_\tau$ to be the standard Levi corresponding to the partition $(r_1m_1, \ldots, r_km_k)$ where $r_i = |[\zeta _i]|$.

2.6 Deformation rings

Let $\overline {\rho }$ be an $\mathbb {F}$-point of $\mathfrak {X}^{\hat {G}}(q)$. Then the formal completion of $\mathfrak {X}^{\hat {G}}(q)$ at $\overline {\rho }$ is

\[ X^{\hat{G}}_{\overline{\rho}} = \operatorname{Spf} R^{\hat{G}}_{\overline{\rho}} \]

where $R^{\hat {G}}_{\overline {\rho }}$ is the universal framed deformation ring of $\overline {\rho }$. The morphism $\mathfrak {X}^{\hat {G}}(q) \rightarrow \mathcal {S}^{\hat {G}}(q)$ gives an $\mathbb {F}$-point $\overline {s} \in \mathcal {S}^{\hat {G}}(q)$, and we let $S^{\hat {G}}_{\overline {s}}$ be the formal completion of $\mathcal {S}^{\hat {G}}(q)$ at $\overline {s}$. Then we have a morphism

\[ \mathrm{ch}_I : X^{\hat{G}}_{\overline{\rho}} \rightarrow S^{\hat{G}}_{\overline{s}}. \]

Remark 2.13 Any continuous representation $\rho : W_t \rightarrow {\rm GL}_n(A)$ for a finite ring $A$ has a unique extension to a continuous representation of $G_t$. The deformation ring of $\overline {\rho }$ is therefore the same as the deformation ring of its unique extension to $G_t$, which is the object more usually considered.

We will compute the local deformation rings at specially chosen points of the special fibre.

Definition 2.14 Let $f \geqslant 1$ be an integer. We say that a ${\hat {G}}$-parameter $\overline {\rho } : W_t \rightarrow {\hat {G}}(\mathbb {F})$ is $f$-distinguished if there is a Levi subgroup ${\hat {M}} \subset {\hat {G}}$ such that $\overline {\rho }$ factors through an ${\hat {M}}$-parameter $\overline {\rho }_{\hat {M}} : W_t \rightarrow {\hat {M}}(\mathbb {F})$ with the following properties:

1. (i) $\overline {\rho }_{\hat {M}} |_{I_{t}}$ is a discrete inertial parameter;

2. (ii) $Z_{G_\mathbb {F}}(\overline {\rho }(\phi ^{f})_s) \subset {\hat {M}}_{\mathbb {F}}$.

Here $Z_{G_\mathbb {F}}(\overline {\rho }(\phi ^{f})_s)$ is the centralizer of the semisimple part $\overline {\rho }(\phi ^{f})_s$ of $\overline {\rho }(\phi ^{f})$.

We say that ${\hat {M}}$ is an $f$-allowable Levi subgroup for $\rho$.

It is useful to rewrite this in coordinates. If $\hat {M}$ is a standard Levi subgroup ${\rm GL}_{n_1} \times \ldots \times {\rm GL}_{n_r}$ then $\overline {\rho }$ is $f$-distinguished with $f$-allowable Levi $\hat {M}$ if $\overline {\rho }(\sigma ), \overline {\rho }(\phi ) \in \hat {M}(\mathbb {F})$, if $\overline {\rho }(\sigma )$ is a regular element of $\hat {M}(\mathbb {F})$, and if

\[ \overline{\rho}(\phi^{f}) = \begin{pmatrix} A_1 & & \\ & \ddots & \\ & & A_r\end{pmatrix} \]

with $A_i \in {\rm GL}_{n_i}(\mathbb {F})$ such that the $A_i$ have pairwise disjoint sets of eigenvalues.

The utility of this definition is roughly that we may canonically conjugate lifts of $\overline {\rho }(\phi ^{f})$ to lie in ${\hat {M}}$. For $f$ large enough, this will force the entire lift of $\overline {\rho }$ to land in $\hat {M}$ as well, and so we can reduce to calculating deformation rings for discrete parameters.

Definition 2.15 If $\hat {G}$ has rank $n$, then an integer $f \geqslant 1$ is large enough for $\hat {G}$ if

\[ v_l(q^{f} - 1) > v_l(n!). \]

The purpose of the next three sections is to prove the following theorem.

Theorem 2.16 Let $f \geqslant 1$ be large enough for $\hat {G}$, and suppose that $\overline {\rho } : W_t \rightarrow {\hat {G}}(\mathbb {F})$ is $f$-distinguished. Let ${\hat {M}}$ be an allowable Levi subgroup for $\overline {\rho }$. Then there is a formally smooth morphism

\[ \pi:X^{\hat{G}}_{\overline{\rho}} \rightarrow S^{\hat{M}}_{\overline{s}} \]

such that the triangle

commutes.

The following lemma will be used later to deduce a Breuil–Mézard-type result. It is not used in the proof of Theorem 2.16.

Lemma 2.17 Let $f$ be large enough for $\hat {G}$. Every irreducible component of $\mathfrak {X}^{\hat {G}}(q)_\mathbb {F}$ contains an $f$-distinguished $\mathbb {F}'$-point $\overline {\rho }$ that lies on no other component, for some finite extension $\mathbb {F}'/\mathbb {F}$.

Proof. Consider an irreducible component labelled by the inertial ${\hat {G}}$-parameter $\tau$. Let ${\hat {M}}$ be a Levi subgroup such that $\tau$ factors through a discrete inertial ${\hat {G}}$-parameter $\tau _{\hat {M}}$ (one exists, by Lemma 2.12). We may extend $\tau$ to an ${\hat {M}}$-parameter $\overline {\rho }_{\hat {M}}$, and so a ${\hat {G}}$-parameter $\overline {\rho }$. Then $\overline {\rho }$ satisfies the first part of Definition 2.14, with $\hat {M}$ as the allowable Levi. It may not be the case that $Z_{\hat {G}}(\overline {\rho }(\phi ^{f})) \subset \hat {M}$, but by twisting $\overline {\rho }_{\hat {M}}$ by a sufficiently general element of $Z({\hat {M}})(\mathbb {F}')$, for some extension $\mathbb {F}'/\mathbb {F}$, this will hold. Then, after this twist, $\overline {\rho }$ is $f$-distinguished with allowable Levi ${\hat {M}}$.

That $\overline {\rho }$ lies on a unique irreducible component can be seen directly, but it is easier to appeal to Theorem 2.16, which implies that the special fibre of $X^{\hat {G}}_{\overline {\rho }, \mathbb {F}'}$ has a unique irreducible component since the same is true for $S^{\hat {M}}_{\overline {s}}$, whose special fibre is local Artinian. As the completion map $\mathcal {O}_{\mathfrak {X}^{\hat {G}}(q)_\mathbb {F}, \overline {\rho }} \rightarrow R^{\hat {G}}_{\overline {\rho }} \otimes \mathbb {F}$ is faithfully flat, it follows that $\mathfrak {X}^{\hat {G}}(q)_\mathbb {F}$ has a unique irreducible component containing $\overline {\rho }$ as required.

Remark 2.18 It follows that Theorem 2.16 describes the local structure of $\mathfrak {X}^{\hat {G}}(q)$ at a general point of its special fibre. By combining this with the Clifford theory arguments of [CHT08] § 2.4.4, it would be possible to obtain a similar result for the entire moduli space of Langlands parameters (as constructed in [DHKM20]).

2.7 Diagonalization

Lemma 2.19 Suppose that $X$, $S$ and $F$ are objects of $\mathcal {FS}_{\mathcal {O}}$ and that we have morphisms $j : F \rightarrow S$, $p :F \rightarrow X$ and $s : X \rightarrow F$ such that:

1. (i) $p \circ s = \mathrm {id}_X$; and

2. (ii) $j \circ s \circ p$ is formally smooth.

Then $i = j \circ s$ is formally smooth.

Proof. Define $j' : F \rightarrow S$ by $j' = i \circ p = j\circ s \circ p$. If $F$ and $X$ are made into formal schemes over $S$ via $j'$ and $i$ respectively, then $p$ and $s$ are maps of formal schemes over $S$. Indeed, $i \circ p = j'$ by definition, and $j' \circ s = i \circ p \circ s = i$ by the hypothesis that $p \circ s = \mathrm {id}_X$.

Now, as $j'$ is formally smooth by hypothesis, we are (after converting to objects of $\mathcal {C}_{\mathcal {O}}^{\wedge }$ and reversing all arrows) in the situation of [Sta, Lemma 00TL], taking into account the remark following that lemma. The result follows.

Lemma 2.20 (Diagonalization lemma)

Let $\overline {g} \in {\hat {G}}(\mathbb {F})$ have semisimple part $\overline {s}$, and let ${\hat {M}}$ be a Levi subgroup of ${\hat {G}}$ such that ${\hat {M}}_\mathbb {F} = Z_{G_\mathbb {F}}(\overline {s})$; note that $\overline {g} \in {\hat {M}}(\mathbb {F})$. Let ${\hat {L}} \subset {\hat {G}}$ be a Levi subgroup containing ${\hat {M}}$. Let $c : {\hat {L}} \times {\hat {G}} \rightarrow {\hat {G}}$ be the conjugation map $c(\delta,\gamma ) = \gamma \delta \gamma ^{-1}$.

1. (i) There is a section

   \begin{align*} \alpha = \delta \times \gamma: {\hat{G}}_{\overline{g}}^{\wedge}\rightarrow {\hat{L}}_{\overline{g}}^{\wedge} \times {\hat{G}}_e^{\wedge} \end{align*}
   to the completion of $c$ such that the map $\delta : G_{\overline {g}}^{\wedge } \rightarrow {\hat {L}}_{\overline {g}}^{\wedge }$ is formally smooth.

2. (ii) Suppose that $A \in \mathcal {C}_{\mathcal {O}}^{\wedge }$ and that $g \in {\hat {L}}(A)$ is a lift of $\overline {g}$. Suppose that $q$ is an integer such that $\overline {s}^{q}$ and $\overline {s}$ are conjugate as elements of ${\hat {L}}(\mathbb {F})$. Then

   \[ \{h \in {\hat{G}}(A) : hgh^{-1} = g^{q}\} \subset {\hat{L}}(A). \]

Proof. (i) We may suppose that ${\hat {G}} = {\rm GL}_n$ and that ${\hat {L}} = {\rm GL}_{n_1} \times \ldots \times {\rm GL}_{n_r}$ for some natural numbers $n_i$. Let

\[ \overline{g} = \begin{pmatrix} X_1 & & \\ & \ddots & \\ & & X_r\end{pmatrix} \]

for some matrices $X_i \in {\rm GL}_{n_i}(\mathbb {F})$ with characteristic polynomials $\overline {P}_i$. By the assumption that ${\hat {M}} \subset {\hat {L}}$, the polynomials $\overline {P}_i$ are pairwise coprime. Let $A \in \mathcal {C}_\mathcal {O}$ and let $g \in {\hat {G}}(A)$ be a lift of $\overline {g}$. Let $P$ be the characteristic polynomial of $g$. By Hensel's lemma, $P$ factorizes uniquely as a product $P = P_1 \ldots P_r$ with each $P_i$ a monic lift of $\overline {P}_i$. It follows that for each $i$ we may find a monic polynomial $R_i$ such that

1. – $\prod _{j \neq i} P_j \mid R_i$ and

2. – $R_i \equiv I_{n_i} \mod P_i$.

The matrices $R_i(g)$ are then an orthogonal system of idempotents, and define a direct sum decomposition of $A^{n}$ lying above the decomposition of $\mathbb {F}^{n}$ associated to ${\hat {L}}$. If $e^{(1)}_1, \ldots, e^{(1)}_{n_1}, e^{(2)}_{1}, \ldots, e^{(2)}_{n_2}, \ldots,e^{(r)}_{1}, \ldots e^{(r)}_{n_r}$ is the standard basis of $A^{n}$ then set $f^{(i)}_j = R_i(g)e^{(i)}_j$. The basis $(f^{(i)}_j)_{i,j}$ is then a basis of $A^{n}$ lifting the standard basis of $\mathbb {F}^{n}$ and with respect to which the action of $g$ is a block diagonal. Letting $\gamma$ be the change of basis matrix from $e_j^{(i)}$ to $f_j^{(i)}$, we have that $\gamma \in 1 + M_n(\mathfrak {m}_A)$ and $\gamma ^{-1} g \gamma \in {\hat {L}}(A)$. This construction is functorial and we obtain the morphism

\begin{align*} \alpha : {\hat{G}}^{\wedge}_{\overline{s}} &\rightarrow {\hat{L}}^{\wedge}_{\overline{s}} \times {{\hat{G}}}^{\wedge}_{e} \\ g &\mapsto (\delta = \gamma^{-1} g \gamma, \gamma) \end{align*}

that is evidently a section of $c$.

Let $\pi : {\hat {L}}^{\wedge }_{\overline {s}} \times {\rm GL}_{n, e}^{\wedge }\rightarrow {\hat {L}}^{\wedge }_{\overline {s}}$ be the projection so that

\[ \delta = \pi \circ \alpha : {\hat{G}}^{\wedge}_{\overline{s}} \rightarrow {\hat{L}}^{\wedge}_{\overline{s}}. \]

We will apply Lemma 2.19 to the diagram

and deduce that $\delta$ is formally smooth, as required. To apply Lemma 2.19 we must show that $\delta \circ c$ is formally smooth. Following carefully through the construction of $\alpha$, one finds that this map is

\[ \delta \circ c : (g, \gamma) \mapsto \gamma_{\hat{L}} g\gamma_{\hat{L}}^{-1} \]

where $\gamma _{\hat {L}}$ is the truncation of $\gamma$ obtained by setting all of the matrix entries outside of ${\hat {L}}$ equal to zero. This is formally smooth: we can write it as a composite

\[ (g, \gamma) \mapsto (g, \gamma_{\hat{L}}) \mapsto (\gamma_{\hat{L}}g\gamma_{\hat{L}}^{-1},\gamma_{\hat{L}}) \mapsto \gamma_{\hat{L}} g \gamma_{\hat{L}}^{-1} \]

in which the first and third maps are formally smooth, and the second map is an isomorphism.

(ii) In the notation of proof of the previous part, the assumption on $\overline {s}$ implies that $R_i(g^{q}) = R_i(g)$ for each $i$. Then any element $h \in {\hat {G}}(A)$ such that $h^{-1}gh= g^{q}$ commutes with the projectors $R_i(g)$. It follows that $h$ preserves the direct sum decomposition of $A^{n}$ associated to the $R_i(g)$; since $g \in {\hat {L}}$, this is exactly the direct sum composition corresponding to ${\hat {L}}$, whence $h \in {\hat {L}}(A)$.

2.8 Inertially unipotent deformation rings

Fix standard topological generators $\sigma, \phi$ of $W_t$. We say that a representation $\overline {\rho } : W_t \rightarrow \hat {G}(\mathbb {F})$ is inertially unipotent if $\overline {\rho }(\sigma )$ is unipotent; this is independent of the choice of $\sigma$. For this section, we suppose that $\overline {\rho } : W_t \rightarrow \hat {G}(\mathbb {F})$ is inertially unipotent, and that it is $f$-distinguished with $\hat {M}$ an $f$-allowable subgroup.

If $\hat {G} = {\rm GL}_{n, \mathcal {O}}$ and ${\hat {M}}$ is an $f$-allowable Levi subgroup for $\overline {\rho }$, then after conjugating, we may assume that

(4)\begin{equation} \overline{\rho}(\sigma) = \begin{pmatrix} J_{n_1}(1) & & \\ & \ddots & \\ & & J_{n_r}(1)\end{pmatrix}\end{equation}

where $r, n_1, \ldots, n_r \in \mathbb {N}$, and that the standard Levi subgroup ${\hat {M}} = \prod _{i=1}^{r} {\rm GL}_{n_i}$ is an $f$-allowable subgroup for $\overline {\rho }$.

Lemma 2.21 Suppose that $A \in \mathcal {C}_{\mathcal {O}}$ and that $\rho : W_t \rightarrow {\hat {G}}(A)$ is a lift of $\overline {\rho }$ such that $\rho (\phi ) \in {\hat {M}}(A)$. Then $\rho (\sigma ) \in {\hat {M}}(A)$.

Proof. This is similar to Lemma 7.9 of [Sho18]. We may and do assume that $\hat {G} = {\rm GL}_n$ and that $\overline {\rho }$ and $\hat {M}$ have the form given by (4). Write $\Sigma = \rho (\sigma )$ and $\Phi = \rho (\phi )$. By our assumptions, we have that

\[ \Phi^{f} = \begin{pmatrix} \Phi_1 & & \\ & \ddots & \\ & & \Phi_{r}\end{pmatrix} \]

is block diagonal with $\Phi _i \in {\rm GL}_{n_i}(A)$ for each $i$. We write

\[ \Sigma = \begin{pmatrix} \Sigma_{11} & \Sigma_{12} & \ldots \\ \Sigma_{21} & \Sigma_{22} & \ldots \\ \vdots & \vdots & \ddots \\ \\ \ldots & \Sigma_{r(r-1)} & \Sigma_{rr}\end{pmatrix} \]

for $\Sigma _{ij} \in M_{n_i \times n_j}(A)$. Let $I \subset \mathfrak {m}_A$ be the ideal generated by all the entries of all $\Sigma _{ij}$ with $i \neq j$.

We write $\Sigma = 1 + N$ for $N \in M_n(A)$ a lift of a nilpotent matrix. Then we have

\begin{align*} \Sigma^{q^{f}} & = (1 + N)^{q^{f}} \\ &= 1 + q^{f}N + \sum_{i=2}^{q^{f}} \Big(\!\!\begin{array}{c}{q^{f}}\\ {i}\end{array}\!\!\Big) N^{i}. \end{align*}

By the assumption that $f$ is large enough for $\hat {G}$, we have $q^{f} \equiv 1 \mod \mathfrak {m}_A$ and $\big (\!\begin {smallmatrix}{q^{f}}\\ {i}\end {smallmatrix}\!\big ) \in \mathfrak {m}_A$ for $1 \leqslant i \leqslant n$; by the assumption that $\overline {\rho }(\sigma )$ is unipotent we have

\[ N^{n} \equiv (\overline{\rho}(\sigma) - 1)^{n} = 0 \mod \mathfrak{m}_A. \]

We therefore obtain, for each $1 \leqslant i, j \leqslant r$, that

\[ (\Sigma^{q^{f}})_{ij} \equiv \Sigma_{ij} \mod \mathfrak{m}_A I. \]

However, from the equation $\Phi ^{f}\Sigma = \Sigma ^{q^{f}}\Phi ^{f}$ we get

\begin{align*} \Phi_i \Sigma_{ij} &= (\Sigma^{q^{f}})_{ij}\Phi_j \\ &\equiv \Sigma_{ij} \Phi_j \mod \mathfrak{m}_A I. \end{align*}

It follows that

\[ P(\Phi_i) \Sigma_{ij}\equiv \Sigma_{ij}P(\Phi_j) \mod \mathfrak{m}_AI \]

for any polynomial $P \in A[X]$. If $P_i$ is the characteristic polynomial of $\Phi _i$ then, by the assumption that $\overline {\rho }$ is $f$-distinguished and $\hat {M}$ is an $f$-allowable Levi, $P_i$ and $P_j$ are coprime modulo $\mathfrak {m}_A$. Thus there are polynomials $Q_1, Q_2 \in A[X]$ such that $Q_1P_i +Q_2 P_j = 1$, and $P_j(\Phi _i)$ is invertible with inverse $Q_2(\Phi _i)$. But

\begin{align*} P_j(\Phi_i) \Sigma_{ij} &\equiv \Sigma_{ij}P_j(\Phi_j) \\ &= 0 \mod \mathfrak{m}_A I \end{align*}

by the Cayley–Hamilton theorem and so $\Sigma _{ij} \equiv 0 \mod \mathfrak {m}_AI$. As this holds for all $i \neq j$, we see that $I \subset \mathfrak {m}_A I$. By Nakayama's lemma, $I = 0$, so that $\Sigma _{ij} = 0$ for all $i \neq j$. Thus $\Sigma \in {\hat {M}}(A)$, as required.

Corollary 2.22 There is a formally smooth retraction

\[ X_{\overline{\rho}}^{\hat{G}} \rightarrow X_{\overline{\rho}}^{\hat{M}}. \]

By a retraction, we mean a left inverse to the natural inclusion.

Proof. Let $X_{\overline {\rho }}^{\Phi \in {\hat {M}}} \subset X_{\overline {\rho }}^{\hat {G}}$ be the closed subformal scheme on which $\rho (\phi ) \in {\hat {M}}$. It follows from part (1) of Lemma 2.20, and the assumption that $\overline {\rho }$ is $f$-distinguished with ${\hat {M}}$ an $f$-allowable subgroup, that there is a retraction $X_{\overline {\rho }}^{\hat {G}} \rightarrow X_{\overline {\rho }}^{\Phi \in {\hat {M}}}$. But Lemma 2.21 shows that the inclusion $X_{\overline {\rho }}^{\hat {M}} \subset X_{\overline {\rho }}^{\Phi \in {\hat {M}}}$ is actually an equality, and the corollary follows.

In what follows, we denote by $\overline {e}$ the identity point of $\hat {T}(\mathbb {F})$, and use the same notation for the corresponding points of $\hat {T}/W_{\hat {M}}$, $\mathcal {S}^{\hat {M}}$, and so on. Let $S^{\hat {M}}_{\overline {e}}$ be the completion of $\mathcal {S}^{\hat {M}}(q)$ at $\overline {e}$, and for $Z$ any of $\hat {T}$, $\hat {T}/W_{\hat {M}}$ or $(\hat {T}/W_{\hat {M}})^{q}$ let $Z_{\overline {e}}$ be the completion of $Z$ at $\overline {e}$.

Theorem 2.23 Recall our running assumptions that $\overline {\rho }$ is inertially unipotent and $f$-distinguished with $f$-allowable subgroup $\hat {M}$. The map

\[ \mathrm{ch}_{I} : X_{\overline{\rho}}^{\hat{M}} \rightarrow S^{\hat{M}}_1 \]

is formally smooth.

Proof. This is an elaboration of the proof of [Sho18, Proposition 7.10], an argument which is also used in [Hel20, § 5].

We can and do immediately reduce to the case that ${\hat {M}} = {\rm GL}_n$. Then $\overline {\rho }(\sigma )$ is a regular unipotent element of ${\hat {M}}(\mathbb {F})$ and we conjugate so that it is equal to the Jordan block $J_n(1)$.

Let $\hat {T}$ be a split maximal torus in $\hat {M}$. Our chosen generator $\sigma \in I_t$ identifies $S^{\hat {M}}_{\overline {e}}$ with the $q$-fixed points $(\hat {T}/W_{\hat {M}})_{\overline {e}}^{q}$. Let

\[ Z = \hat{T}_{\overline e} \times_{(\hat{T}/W_{\hat{M}})_{\overline e}} (\hat{T}/W_{\hat{M}})_{\overline e}^{q}. \]

For $A \in \mathcal {C}_\mathcal {O}$, an $A$-point of $Z$ is the same as a tuple $(t_1, \ldots, t_n)$ of elements of $1 + \mathfrak {m}_A$ such that

\[ \prod_{i=1}^{n} (X - t_i) = \prod_{i=1}^{n} (X - t_i^{q}). \]

Let $Y$ be the closed formal subscheme of $X^{\hat {M}}_{\overline {\rho }}$ whose $A$-points are lifts $\rho$ of $\overline {\rho }$ for which

\[ \overline{\rho}(\sigma) = \begin{pmatrix} a_1 & 1 & 0 & 0 & \ldots \\ 0 & a_2 & 1 & 0 & \ldots \\ 0 & 0 & a_3 & 1 & \ldots \\ \vdots & \vdots & \ddots & \ddots & \ddots \end{pmatrix} \]

for some $a_1, \ldots, a_n \in 1 + \mathfrak {m}_A$. Then there is a morphism

\[ Y \rightarrow \hat{T} \]

taking $\rho$ to $(a_1, \ldots, a_n)$. Since $\rho (\sigma )$ is conjugate to $\rho (\sigma )^{q}$, we see that this map actually factors through a map $\delta : Y \rightarrow Z$. The diagram

commutes and so we have a morphism $f : Y \rightarrow Z \times _{(\hat {T}/W_{\hat {M}})^{q}_{\overline e}} X_{\overline {\rho }}^{\hat {M}}$. I now make the following claims.

1. (1) There is a formally smooth morphism of $Z$-formal schemes

   \[ s : X^{\hat{M}}_{\overline{\rho}} \times_{(\hat{T}/W_{\hat{M}})^{q}_{\overline e}} Z \rightarrow Y. \]

2. (2) The morphism $\delta : Y \rightarrow Z$ is formally smooth.

It follows from these claims, proved below, that the map $\mathrm {ch}_I : X^{\hat {M}}_{\overline {\rho }} \rightarrow (\hat {T}/W_{\hat {M}})^{q}_{\overline e}$ is formally smooth after base change to $Z$. Since $Z \rightarrow (\hat {T}/W_{\hat {M}})^{q}_{\overline {e}}$ is finite flat, this implies (by [DG61, Corollaire 0.19.4.6]) that $X^{\hat {M}}_{\overline {\rho }} \rightarrow (\hat {T}/W_{\hat {M}})^{q}_{\overline e}$ is formally smooth as required.

Proof of claim (1). Let $\mathcal {P}$ be the completion at the identity of the subgroup $P$ of $\hat {M} = {\rm GL}_n$ consisting of matrices whose first column is $(1, 0, \ldots, 0)^{t}$. We have a morphism

\[ \alpha : Y \times \mathcal{P} \rightarrow X_{\overline{\rho}}\times_{(\hat{T}/W_{\hat{M}})^{q}_{\overline e}} Z \]

defined by

\[ \alpha : (\rho, \gamma) \mapsto (\gamma \rho \gamma^{-1}, \delta(\rho)). \]

We show now that it is an isomorphism. Define a morphism

\[ \beta : X_{\overline{\rho}}\times_{(T/W_{\hat{M}})^{q}_{\overline e}} Z \rightarrow Y \times \mathcal{P} \]

on $A$-points as follows. Suppose given an $A$-point $(\rho, (t_1, \ldots, t_n))$ of $(X_{\overline {\rho }}\times _{(T/W_{\hat {M}})^{q}_{\overline e}} Z)$; then $(T - a_1)(\ldots )(T - a_n) = \mathrm {ch}_{\rho (\sigma )}(T)$. Let $e_1, \ldots, e_n$ be the standard basis for $A^{n}$ and let $f_1, \ldots, f_n$ be defined recursively by:

1. (i) $f_1 = e_1$;

2. (ii) $f_{i + 1} = (\rho (\sigma ) - a_i) f_i$.

Let $\gamma$ be the matrix (with respect to the standard basis) such that $\gamma (e_i) = f_i$. Then $\gamma$ defines a point of $\mathcal {P}(A)$, as $f_1 = e_1$ and, by assumption on $\overline {\rho }$, $f_i \equiv e_i \mod \mathfrak {m}_A$. Note that

\[ \rho(\sigma)(f_i) = f_{i+1} + a_if_i \]

for $1 \leqslant i \leqslant n-1$, and

\begin{align*} \rho(\sigma)f_n &= a_nf_n + (\rho(\sigma) - a_n)f_n \\ &= a_nf_n + \prod_{i=1}^{n} (\rho(\sigma) - a_n)f_n \\ &= a_n f_n \end{align*}

by the Cayley–Hamilton theorem and the assumption on $(a_1, \ldots, a_n)$. It follows that $\gamma ^{-1} \rho \gamma$ defines an $A$-point of $Y$ lying above the $A$-point $(a_1, \ldots, a_n)$ of $Z$.

We therefore define

\[ \beta\big( \rho, (a_1, \ldots, a_n)\big) = (\gamma^{-1} \rho \gamma, \gamma). \]

We evidently have $\alpha \circ \beta = \mathrm {id}$, and one checks directly from the constructions that $\beta \circ \alpha = \mathrm {id}$. So $\alpha$ and $\beta$ are isomorphisms, as required. The map $s$ of claim (1) is then just the composition of $\beta$ with projection to $Y$.

Proof of claim (2). Let $Y \rightarrow Z \times (\mathbb {A}^{n})_{\overline {e}_1}^{\wedge }$ be the morphism $\rho \mapsto (\delta (\rho ), \rho (\phi )(e_1))$. I claim that this is an isomorphism. To see injectivity (at the level of $A$-points), note that for $i \geqslant 2$ we can recover $\rho (\phi )(e_i)$ inductively from the formula

\begin{align*}\rho(\phi)(e_{i+1}) &= \rho(\phi)(\rho(\sigma) - a_i)(e_i) \\ &= (\rho(\sigma)^{q} - a_i)\rho(\phi)(e_i). \end{align*}

For surjectivity, note that the above inductive formula certainly determines a lift $\Phi$ of $\overline {\rho }(\phi )$ with given $\Phi (e_1)$, and we have only to check that $\Phi \rho (\sigma ) = \rho (\sigma )^{q} \Phi$ holds. For $i < n$, we have

\begin{align*}\Phi \rho(\sigma)(e_i) &= \Phi (a_i e_i + e_{i+1}) \\ &= \Phi(a_ie_i) + (\rho(\sigma)^{q} - a_i) \Phi (e_i) \\ &= \rho(\sigma)^{q} \Phi(e_i) \end{align*}

as required. For $i = n$, note that (writing $\Sigma = \rho (\sigma )$)

\begin{align*} (\rho(\sigma^{q}) - a_n)\Phi(e_n) &= (\Sigma^{q} - a_n)(\Sigma^{q} - a_{n-1}) \Phi (e_{n-1})\\ &= \ldots \\ &= (\Sigma^{q} - a_n)(\Sigma^{q} - a_{n-1})( \ldots)(\Sigma^{q} - a_1) \Phi(e_1) \\ &= \mathrm{ch}_{\Sigma}(\Sigma^{q})\Phi(e_1) \\ &= \mathrm{ch}_{\Sigma^{q}}(\Sigma^{q})\Phi(e_1) \\\textrm {(by our assumption on $(a_1, \ldots, a_n)$)} &= 0. \end{align*}

It follows that

\[ \Phi \Sigma (e_n) = \Phi (a_ne_n) = \Sigma^{q} \Phi (e_n), \]

as required.

Corollary 2.24 Let $\overline {\rho }$ and ${\hat {M}}$ be as above. Then there is a formally smooth morphism

\[ X_{\overline{\rho}}^{\hat{G}} \rightarrow S^{\hat{M}}_{\overline e} \]

whose composition with the inclusion $X_{\overline {\rho }}^{\hat {M}} \hookrightarrow X_{\overline {\rho }}^{\hat {G}}$ is $\mathrm {ch}_I$.

Proof. Immediate from Corollary 2.22 and Theorem 2.23.

2.9 Reduction to the unipotent case

We explain how to deduce Theorem 2.16 from the inertially unipotent case (Corollary 2.24). The argument is essentially that of [CHT08, Corollary 2.13] and [Cho17, Proposition 2.6], albeit phrased slightly differently.

Fix standard topological generators $\sigma, \phi$ of $W_t$. Suppose that ${\hat {G}}$ is as above, that ${\hat {M}}$ is a Levi subgroup containing a split maximal torus $\hat {T}$, and that $f$ is large enough for $\hat {G}$. Let $n = \operatorname {rk}(\hat {G})$.

Suppose that $\overline {\rho } : W_t \rightarrow {\hat {G}}(\mathbb {F})$ is $f$-distinguished with $f$-allowable subgroup ${\hat {M}}$. Write $\overline {\rho }|_{I_t} = \tau _s \tau _u$ with $\tau _s$ semisimple and $\tau _u$ unipotent. Up to conjugation, using assumption (3), we may and do assume that $\tau _s$ has image in ${\hat {T}}(\mathbb {F})$. Let $\tilde {\tau }_s$ be the unique lift of $\tau _s$ to ${\hat {T}}(\mathcal {O})$ having order coprime to $l$.

First, we reduce to the case that the eigenvalues of $\tau _s(\sigma )$ form a single orbit under the $q$-power map. Let

\[ {\hat{L}}_0 = \{g \in {\hat{G}} : g \tilde{\tau}_s g^{-1} = \tilde{\tau}_s^{q^{i}} \text{for some $i \in \mathbb{N}$}\}, \]

so that ${\hat {L}}_0 = Z_{\hat {G}}(\tilde {\tau }_s) \rtimes \langle w \rangle$ for some element $w$ of the Weyl group $W$. Finally, let

\[ {\hat{L}} = Z_{\hat{G}}(Z({\hat{L}}_0)), \]

a Levi subgroup of ${\hat {G}}$. Then certainly $Z_{\hat {G}}(\tilde {\tau }_s) \subset {\hat {L}}$. By Lemma 2.20(1), there is a morphism $\gamma :{\hat {G}}_{\overline {\rho }(\sigma )}^{\wedge } \rightarrow {\hat {G}}_e^{\wedge }$ such that conjugating by $\gamma (\rho (\sigma ))$ defines a formally smooth morphism

\begin{align*}X_{\overline{\rho}}^{\hat{G}} &\rightarrow X_{\overline{\rho}}^{\sigma \in {\hat{L}}} \\ \rho &\mapsto \gamma(\rho(\sigma))^{-1} \rho \gamma(\rho(\sigma)) \end{align*}

where the space on the right is the closed formal subscheme of $X^{\hat {G}}_{\overline {\rho }}$ on which $\rho (\sigma ) \in {\hat {L}}$ (which is clearly independent of the choice of $\sigma$). By part (2) of the same lemma,

\[ X_{\overline{\rho}}^{\sigma \in {\hat{L}}} = X_{\overline{\rho}}^{\hat{L}}. \]

It is therefore enough to prove Theorem 2.13 with ${\hat {G}}$ replaced by ${\hat {L}}$; note that $\overline {\rho }$ is still $f$-distinguished as a representation valued in ${\hat {L}}$. Since ${\hat {L}}$ is a product of general linear groups, it in fact suffices to prove Theorem 2.13 in the case that ${\hat {G}} = {\hat {L}} = {\rm GL}_n$ for some $n$. Then we have that $Z({\hat {L}}_0) = Z({\hat {G}})$, which happens if and only if the eigenvalues of $\tau (\sigma )$ form a single orbit under the $q$-power map. So, up to conjugating $\overline {\rho }$, we may assume that $n = rd$ for some integers $r$ and $d$, where $d$ is the smallest natural number with $\tau _s^{q^{d}} = \tau _s$, and that

(5)\begin{equation} \tau = \operatorname{diag}(\tau_r, \tau_r^{q}, \ldots, \tau_r^{q^{d-1}})\end{equation}

for some homomorphism $\tau _r : I_t \rightarrow {\rm GL}_r(\mathbb {F})$ with scalar semisimplification. From now on we assume $\tau$ has this form. We also regard ${\rm GL}_r$ as being embedded in ${\rm GL}_n$ in the ‘top left corner’.

Let $W_t^{(d)}$ be the subgroup of $W_t$ generated by $I_t$ and $\phi ^{d}$. Our next step is to show that deforming $\overline {\rho }$ is the same as deforming the ‘top left part’ of the restriction to $W_t^{(d)}$.

Let

\[ {\hat N} = Z_{\hat{G}}(\tilde{\tau}_s). \]

Then $\hat {N}$ is the standard Levi subgroup with block sizes $(r, r, \ldots, r)$. Let $\pi : {\hat N} \rightarrow {\rm GL}_r$ be the map that forgets the entries outside of the first copy of ${\rm GL}_r \subset {\hat N}$. Choose $w \in W$ such that $\tau _s^{q} = w\tau _s w^{-1}$ and such that $w^{d} = e$. Specifically, with the above form of $\tau$ we can take $w$ to be the block matrix (with $r \times r$ blocks)

\[ w = \begin{pmatrix} 0 & I & 0 & \ldots & 0 \\ 0 & 0 & I & \ldots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \ldots & I \\ I & 0 & 0 & \ldots & 0 \end{pmatrix}. \]

Then $\overline {\rho }(W_t^{(d)}) \subset {\hat N}(\mathbb {F})$. Let $X_{\overline {\rho }}^{\sigma \in {\hat N}} \subset X^{\hat {G}}_{\overline {\rho }}$ be the closed formal subscheme on which $\rho (\sigma ) \subset {\hat N}$. Then Lemma 2.20 implies that there is a formally smooth retraction

\[ X_{\overline{\rho}}^{\hat{G}} \rightarrow X_{\overline{\rho}}^{\sigma \in {\hat N}} \]

to the natural inclusion, and that $\rho (\phi ) \in w{\hat N}$ for all $\rho$ on $X_{\overline {\rho }}^{\sigma \in \hat {N}}$. If $\rho : W_t \rightarrow {\hat N}(A) \rtimes \langle w \rangle$ is a continuous representation, then we write $\rho ^{(d)}$ for the representation

\[ \pi \circ \rho|_{W^{(d)}_t} : W^{(d)}_t \rightarrow {\rm GL}_r(A). \]

Lemma 2.25 The map

\[ \rho \mapsto \rho^{(d)} \]

defines a formally smooth morphism $X_{\overline {\rho }}^{\sigma \in {\hat N}} \rightarrow X^{{\rm GL}_r}_{\overline {\rho }^{(d)}}$.

Proof. Let $A \in \mathcal {C}_\mathcal {O}$. For $g \in {\hat N}(A)$ any element, let $g_i$ be the projection onto the $i$th factor of ${\hat N}$ (so $g_i \in {\rm GL}_{r}(A)$). If $\rho$ is an $A$-point of $X_{\overline {\rho }}^{\sigma \in {\hat N}}$, we write $\Sigma$ and $\Phi$ for $\rho (\sigma )$ and $\rho (\phi )$. Any point of $X_{\overline {\rho }}^{\sigma \in {\hat N}}(A)$ has the form $(\Sigma,\Phi = w\Psi )$ for $\Sigma, \Psi \in {\hat N}(A)$ such that $\Psi _i\Sigma _i\Psi _i^{-1} = \Sigma _{i-1}^{q}$ for all $i$ (with indices taken modulo $d$). Note that $(\Phi ^{d})_1 = \Psi _2 \ldots \Psi _d \Psi _1$. Define a morphism

\begin{align*} X^{\sigma \in {\hat N}}_{\overline{\rho}} & \rightarrow X^{{\rm GL}_r}_{\overline{\rho}^{(d)}} \times \prod_{i=2}^{d}{\rm GL}^{\wedge}_{r, \overline{\Psi}_i} \\ (\Sigma, w\Psi) & \mapsto \big((\Sigma_1, (w\Psi)^{d}_1), \Psi_2, \ldots, \Psi_d\big). \end{align*}

This is in fact an isomorphism; we may write down the inverse

\[ \big((\Sigma\zeta^{-1}, \Phi), \Psi_2, \ldots, \Psi_d\big) \mapsto (\Sigma', w\Psi') \]

where $\Sigma '$ is defined by $\Sigma '_1 = \Sigma$ and $\Sigma '_i = \Psi _i^{-1} (\Sigma '_{i-1})^{q}\Psi _i$ for $i \geqslant 2$, and $\Psi '$ is defined by $\Psi '_i = \Psi _i$ for $i \geqslant 2$ and $\Psi '_1 = (\Psi _2\ldots \Psi _d)^{-1}\Phi$. The lemma follows.

We therefore have a formally smooth map

\[ X^{\hat{G}}_{\overline{\rho}} \rightarrow X^{{\rm GL}_r}_{\overline{\rho}^{(d)}}. \]

If we let ${\hat {M}}' = {\hat {M}} \cap {\rm GL}_r$, then we may redo the above arguments with ${\hat {G}}$ replaced by ${\hat {M}}$ and ${\rm GL}_r$ replaced by ${\hat {M}}'$ and obtain a commuting diagram

(6)

in which the horizontal morphisms are formally smooth.

The representation $\overline {\rho }^{(d)} : W_t^{(d)} \rightarrow {\rm GL}_r(\mathbb {F})$ has the property that $\overline {\rho }^{(d)}|I_t$ has semisimplification given by a scalar $\overline {t} : I_t^{(d)} \rightarrow Z({\rm GL}_r(\mathbb {F}))$. Choose an extension of $\overline {t}$ to $W_t^{(d)}$ and let $\theta : W_t^{(d)} \rightarrow Z({\rm GL}_r(\mathcal {O}))$ be its Teichmüller lift. Twisting by $\theta$ gives a bijection between deformations of $\overline {\rho }^{(d)}$ and deformations of $\overline {\rho } ^{(d)} \otimes \theta ^{-1}$, which is unipotent on inertia. We can therefore apply Corollary 2.24, which shows that there is a formally smooth morphism $X^{{\rm GL}_r}_{\overline {\rho }^{(d)}} \rightarrow \mathcal {S}^{\hat {M}'}(q^{d})_{\overline {t}}$ such that the triangle

(7)

commutes.

We may choose an inclusion $\hat {M}' \times \dots \times \hat {M}' \hookrightarrow \hat {M}$, where there are $d$ copies of $\hat {M}'$, such that conjugation by $\overline {\rho }(\phi ) \in \hat {M}$ permutes these copies cyclically. Take $\hat {T}'$ to be a split maximal torus of $\hat {M}'$ and $\hat {T} = \hat {T}' \times \dots \times \hat {T}'$ the split maximal torus of $\hat {M}$ obtained from it. The map

\[ (\overline{t}, \overline{t}^{q}, \ldots, \overline{t}^{q^{d-1}}) : I_t \rightarrow Z(\hat{M}' \times \dots \times \hat{M}')(\mathbb{F}) \hookrightarrow \hat{T}(\mathbb{F}) \]

defines a point $\overline {s}$ of $\mathcal {S}^{\hat {M}}(q)(\mathbb {F})$ which is exactly the point corresponding to $\overline {\rho }|_{I_t}$.

Lemma 2.26 There is an isomorphism

\[ S^{\hat{M}}_{\overline{s}} = \mathcal{S}^{\hat{M}}(q)_{\overline{s}} \xrightarrow{\sim} \mathcal{S}^{{\hat{M}}'}(q^{d})_{\overline{t}} \]

such that the diagram

(8)

commutes.

Proof. We write down the map on $A$-points. This sends the $W_{\hat {M}}$-orbit of $(s_1, s_2, \ldots, s_r)$, where each $s_i : I_t \rightarrow \hat {T}'(A)$ is a lift of $\overline {s}$, to the $W_{{\hat {M}}'}$-orbit of $s_1$. This is an isomorphism; its inverse is the map taking the $W_{{\hat {M}}'}$-orbit of $s_1$ to the $W_{\hat {M}}$-orbit of

\[ (s_1, s_1^{q}, \ldots, s_1^{q^{d-1}}). \]

Proof of Theorem 2.16 Putting the commuting diagrams (6), (7) and (8) together, we obtain a commuting triangle

in which the right-hand vertical morphism is formally smooth, as required.

3. Representations of finite general linear groups

3.1 Dual groups, tori and parameters

We follow [DR09, § 4.3] and give a formulation of Deligne–Lusztig theory that is adapted for our purposes.

Recall that $k$ is the residue field of $F$, of order $q$. Let $G$ be a product of general linear groups over $k$, and let $\mathbb {T}$ be a split maximal torus of $G$ defined over $k$. We fix an $l$-adic coefficient system $(E, \mathcal {O}, \mathbb {F})$. We take $\hat {T}$ and $\hat {G}$ to be a dual torus of $\mathbb {T}$ and dual group of $G$, defined over $\mathcal {O}$. We assume that $E$ is sufficiently large; to be precise, we impose assumption (3). We write $X = X(\mathbb {T}) = \operatorname {Hom}(\mathbb {T}, \mathbb {G}_m)$, $Y = Y(\mathbb {T}) = \operatorname {Hom}(\mathbb {G}_m, \mathbb {T})$, $X(\hat {T}) = \operatorname {Hom}(\hat {T}, \mathbb {G}_m)$, and $Y(\hat {T}) = \operatorname {Hom}(\mathbb {G}_m, \hat {T})$.

By definition, we have fixed isomorphisms

\[ X(\mathbb{T}) = Y(\hat{T}) \]

and

\[ Y(\mathbb{T}) = X(\hat{T}) \]

respecting the natural pairings.

We write $W = W(G,\mathbb {T})$ for the Weyl group of $\mathbb {T}$. It acts on the left on $\mathbb {T}$. We thus obtain left actions on $X(\mathbb {T})$ and $Y(\mathbb {T})$: the former is defined by $w\alpha = \alpha \circ w^{-1}$ and the latter by $w\beta = w \circ \beta$, for all $\alpha \in X(\mathbb {T})$, $\beta \in Y(\mathbb {T})$, $w \in W$. Thus $W$ acts on the left on $Y(\hat {T})$ and $X(\hat {T})$. Let $\hat {W} = W(\hat {G}, \hat {T})$. Then there is an isomorphism $\delta : W \xrightarrow {\sim } \hat {W}$ such that the action of $w$ on $X(\mathbb {T})$ agrees with the action of $\delta (w)$ on $Y(\hat {T})$. We identify $W$ with $\hat {W}$ along this isomorphism. Note that this differs from the anti-isomorphism of [DR09] by an inverse; we find it more convenient to work with a group isomorphism.

Now let $T \subset G$ be another maximal torus, not necessarily split. Choose $g \in G(\overline {k})$ such that $T_{\overline {k}} = g\mathbb {T}_{\overline {k}}g^{-1}$. Then $g^{-1}F(g) \in N(\mathbb {T}_{\overline {k}})$; write $w$ for its image in $W$. This induces a bijection between $G(k)$-conjugacy classes of maximal tori in $G$, and conjugacy classes in $W$. If $w$ is any element of $W$, we write $T_w$ for a choice of torus in the corresponding conjugacy class. If $F$ is the geometric Frobenius morphism over $k$, then the diagram

commutes. Consequently, $\operatorname {ad}_g$ induces an isomorphism $\mathbb {T}(\overline {k})^{wq} \xrightarrow {\sim } T(k)$. Choose $n$ such that $w^{n} = e$ and write $N = 1 + wq + (wq)^{2} + \ldots + (wq)^{n-1} \in \mathbb {Z}[W]$. Then there is an isomorphism

(9)\begin{equation} N :\mathbb{T}(k_n)/(1 - wq) \xrightarrow{\sim} \mathbb{T}(\overline{k})^{wq}. \end{equation}

Recall that $E$ satisfies assumption (3). Then we have isomorphisms

(10)\begin{align} \operatorname{Hom}(\mathbb{T}(k_n), E^{\times}) &\cong \operatorname{Hom}(Y \otimes k_n^{\times}, E^{\times}) \end{align}

(11)\begin{align} & \cong \operatorname{Hom}(k_n^{\times}, \operatorname{Hom}(Y,E^{\times})) \end{align}

(12)\begin{align} & \cong \operatorname{Hom}(k_n^{\times}, \hat{T}(E)), \end{align}

the first isomorphism coming from $\mathbb {T}(k_n) = Y\otimes k_n^{\times }$ and the last from

\[ \hat{T}(E) \cong \operatorname{Hom}(X(\hat{T}), E^{\times}) = \operatorname{Hom}(Y, E^{\times}). \]

The composite of isomorphisms (10)–(12) takes $\theta \in \operatorname {Hom}(\mathbb {T}(k_n), E^{\times }))$ to the element $s \in \operatorname {Hom}(k_n^{\times }, \hat {T}(E))$ such that

\[ y(s(\alpha)) = \theta(y(\alpha)) \]

for all $y \in Y(\mathbb {T}) = X(\hat {T})$ and $\alpha \in k^{\times }_n$. Combining with the isomorphism $N$ from (9), we obtain an isomorphism

\[ \operatorname{Hom}(\mathbb{T}(\overline{k})^{wq}, E^{\times}) \cong \operatorname{Hom}(k_n, \hat{T}(E)^{w = q}). \]

Finally, we compose with the natural surjection $I_t \twoheadrightarrow k_n$ and note that every homomorphism $I_t \rightarrow \hat {T}(E)^{w = q}$ factors through this surjection, so that we have an isomorphism

(13)\begin{equation} \operatorname{Hom}(\mathbb{T}(k_n)^{wq}, E^{\times}) \cong \operatorname{Hom}(I_t, \hat{T}(E)^{w = q}) \end{equation}

that is independent of any choices (of generators for $I_t$, $k_n^{\times }$, or groups of roots of unity in $E$). If we choose, additionally, $n$ to be large enough that $g \in G(k_n)$, and compose isomorphism (13) with the isomorphism $\operatorname {ad}_g : \mathbb {T}_{k_n} \rightarrow T_{k_n}$, we get

\[ \operatorname{Hom}(T(k), E^{\times}) \cong \operatorname{Hom}(I_t, \hat{T}(E)^{w = q}). \]

Remark 3.1 This isomorphism is exactly the restriction to tame inertia of the local Langlands correspondence for unramified tori constructed in [DR09, § 4.3] (over the complex numbers, but the construction works equally well over any field of characteristic zero containing enough roots of unity).

We therefore obtain, for every $T$ and every $\theta \in \operatorname {Hom}(T(k), E^{\times })$, a $W$-conjugacy class of pairs $(w, s)$ where $w \in W$ and $s : I_t \rightarrow \hat {T}(E)^{w = q}$. Then it is easy to check the following lemma.

Lemma 3.2 The above map taking $(T, \theta )$ to $(w, s)$ gives a bijection between

\[ \{\text{conjugacy classes of pairs $(T, \theta)$ : $T$ maximal torus in $G$, $\theta \in \operatorname{Hom}(T(k),E^{\times})$}\} \]

and

\[ \{\text{$W$-conjugacy classes of $(w,s)$ : $w \in W$ and $s \in \operatorname{Hom}(I_t, \hat{T}(E)^{w = q})$}\}. \]

Recall (see, for example, [DM91, Definition 13.2]) that two pairs $(T, \theta )$ and $(T', \theta ')$ are geometrically conjugate if there is some $n \geqslant 1$ and $h \in G(k_n)$ such that $T'_{k_n} = hT_{k_n}h^{-1}$ and

\[ \theta \circ N_{k_n/k} = \theta' \circ N_{k_n/k} \circ \operatorname{ad}_h \]

as characters of $T(k_n)$, where $N_{k_n/k}$ is the norm.

Lemma 3.3 The above map $(T, \theta ) \mapsto s$ induces a bijection between

\[ \{\text{geometric conjugacy classes of pairs $(T, \theta)$}\} \]

and

\[ \{\text{$q$-power stable $W$-orbits of $s \in \operatorname{Hom}(I_t, \hat{T}(E))$}\}. \]

Proof. Let $n$ be such that $w^{n} = 1$ for all $w \in W$. If $T$ is a maximal torus of $G$ and $g \in G(k_n)$ is such that $T_{\overline {k}} = g\mathbb {T}_{\overline {k}}g^{-1}$ and if $w$ is the class of $g^{-1}F(g)$ in $W$, and $N = 1 + qw + \ldots + (qw)^{n-1} \in \mathbb {Z}[W]$, then we have a commuting diagram as follows.

The rightmost horizontal arrows are as above, while the rightmost vertical arrow is the obvious inclusion. Hence geometric conjugacy classes of pairs $(T, \theta )$ are in bijection with $q$-power stable $W$-orbits of $s \in \operatorname {Hom}(I_t, \hat {T}(E))$ (note that such $s$ automatically have image in $\hat {T}(E)[q^{n}-1]$). We see that two pairs $(T, \theta )$ and $(T', \theta ')$ are geometrically conjugate if and only if the corresponding homomorphisms $s$ and $s'$ are in the same $W$-orbit. Thus the map taking the geometric conjugacy class of $(T, \theta )$ to the $W$-orbit of $s$ is well defined and injective. It is surjective by Lemma 3.2.

3.2 Representations of $G(k)$

If $s \in \operatorname {Hom}(I_t, \hat {T}(E))$ is $W$-conjugate to its $q$th power, we write $W(s)$ for the stabilizer of $s$ and

\[ W(s,s^{q}) = \{w \in W: {}^{w}s = s^{q}\}. \]

Thus $W(s,s^{q})$ is a left coset of $W(s)$ in $W$. Note also that $W(s) = W(s^{q})$, so that $W(s)$ acts on $W(s, s^{q})$ by conjugation. Let $\epsilon : W \rightarrow \{\pm 1\}$ be the sign character. For a field $C$ we write $K_C(G(k))$ for the Grothendieck group of representations of $G(k)$ over $C$.

Definition 3.4 (Deligne–Lusztig representations)

Let $(w, s)$ be a pair comprising an element $w$ of $W$ and a homomorphism $s \in \operatorname {Hom}(I_t, \hat {T}(E)^{w = q})$. Then we define a virtual representation $R(w,s)$ of $G(k)$ by

\[ R(w,s) = R^{\theta}_{T} \]

where $(T,\theta )$ corresponds to $(w, s)$ as in Lemma 3.2. Here $R^{\theta }_T$ is the Deligne–Lusztig virtual representation constructed in [DL76].

Definition 3.5 (Generalized Steinberg representations)

Let $s$ be an element of $\operatorname {Hom}(I_t, \hat {T}(E))$, $W$-conjugate to its $q$th power. Define an element

\[ \pi_G(s) \in K_E(G(k)) \otimes \mathbb{Q} \]

by

\[ \pi_G(s) = |W(s)|^{-1}\sum_{w \in W(s,s^{q})} \epsilon(w)R(w,s). \]

Proposition 3.6 The element $\pi _G(s) = K_E(G(k)) \otimes \mathbb {Q}$ is (the class of) an irreducible representation.

Proof. This follows from [DL76, Theorem 10.7(i)]. The formula there states that

(14)\begin{equation} \sum_{(T, \theta) \bmod G(k)} \frac{(-1)^{\operatorname{rk}_k(G) - \operatorname{rk}_k(T)}}{\big\langle R^{\theta}_T, R^{\theta}_T \big\rangle}R^{\theta}_T \end{equation}

is the class of an irreducible representation, where the sum is over all $G(k)$-conjugacy classes of $(T, \theta )$ in the geometric conjugacy class of $s$ (under the correspondence of Lemma 3.3).

We claim first that if $T$ is a maximal torus of $G$ corresponding to $w \in W$, then

\[ (-1)^{\operatorname{rk}_k(G) - \operatorname{rk}_k(T)} = \epsilon(w). \]

Indeed, $\operatorname {rk}_k(T)$ is the dimension of the $(+1)$-eigenspace of $w$ acting on $X(\mathbb {T}) \otimes \mathbb {C}$. Since the eigenvalues of $w$ occur in conjugate pairs, this has the same parity as the difference of $\operatorname {rk}_k(G) = \dim X(\mathbb {T}) \otimes \mathbb {C}$ and the dimension $d$ of the $(-1)$-eigenspace. As $\epsilon (w) = \det (w | X(\mathbb {T})) = (-1)^{d}$, we obtain the claim.

We claim next that $\big \langle R^{\theta }_T, R^{\theta }_T \big \rangle = |Z_{W}(w) \cap W(s')|$ if $(T, \theta )$ corresponds to $(w,s')$. Indeed, we have the formula [DL76, Theorem 6.8]

\[ \big\langle R^{\theta}_T, R^{\theta}_T \big\rangle = |\{v \in W(T)^{F} : {}^{v}\theta = \theta\}|. \]

The identification of $W(T)$ with $W(\mathbb {T}) = W$ via $\operatorname {ad}_g$ identifies $W(T)^{F}$ with $Z_W(w)$ and the stabilizer of $\theta$ with the stabilizer of $s'$, and we have

\[ \big\langle R^{\theta}_T, R^{\theta}_T \big\rangle = |\{v \in Z_W(w) : {}^{v}s' = s'\}| = |Z_{W}(w) \cap W(s')| \]

as required.

We now can rewrite expression (14) as

\[ \sum_{(w,s') \bmod W} \frac{\epsilon(w)}{|Z_W(w) \cap W(s')|} R(w,s') \]

where the sum runs over $W$-conjugacy classes of pairs $(w,s')$ such that $s'$ is $W$-conjugate to $s$ and $w \in W(s', (s')^{q})$. We can conjugate each term $(w, s')$ in this sum so that $s' = s$ and rewrite it as

\[ \sum_{w \in W(s, s^{q}) \bmod W(s)} \frac{\epsilon(w)}{|Z_W(w) \cap W(s)|} R(w,s) \]

where the sum is over $W(s)$-conjugacy classes in $W(s,s^{q})$. Finally, we rewrite this as

\[ \frac{1}{|W(s)|}\sum_{w \in W(s,s^{q}) \bmod W(s)} \frac{|W(s)|}{|Z_W(w) \cap W(s)|} \epsilon(w)R(w,s), \]

which on application of the orbit–stabilizer theorem (to the conjugation action of $W(s)$ on $W(s,s^{q})$) becomes

\[ \frac{1}{|W(s)|}\sum_{w \in W(s,s^{q})} \epsilon(w)R(w,s), \]

as required.

Definition 3.7 Suppose that $\tau : I_t \rightarrow \hat {G}(E)$ is an inertial $\hat {G}$-parameter, and assume that its semisimplification $s$ has image in $\hat {T}(E)$. Then there is a split Levi subgroup $L \subset G$, with dual Levi $\hat {L}\supset \hat {T}$, such that $\tau$ factors through a discrete inertial $\hat {L}$-parameter. Define a representation $\pi _G(\tau )$ of $G$ by

\[ \pi_G(\tau) = \operatorname{Ind}_{L(k)}^{G(k)} \pi_L(s) \]

and note that this is (up to isomorphism) independent of the choice of $L$.

Next we recall some facts about the Gelfand–Graev representation. Let $B$ be a Borel subgroup of $G$ containing the split maximal torus $\mathbb {T}$, and let $U$ be its unipotent radical. Let $\psi : U(k) \rightarrow W(\mathbb {F})^{\times }$ be a character in general position (that is, whose stabilizer in $B/U$ is $ZU/U$).

Definition 3.8 The (integral) Gelfand–Graev representation is

\[ \Gamma_G = \operatorname{Ind}_{U(k)}^{G(k)}\psi. \]

Up to isomorphism, it is independent of the choices of $T, B$, and $\psi$.

If $A$ is a $W(\mathbb {F})$-algebra then we set $\Gamma _{G,A} = \Gamma _G \otimes _{W(\mathbb {F})} A$.

Lemma 3.9 For any $W(\mathbb {F})$-algebra $A$, the representation $\Gamma _{G, A}$ is a projective $A[G(k)]$-module.

Proof. By Frobenius reciprocity, it suffices to show that $A$, with the action of $U(k)$ via $\psi$, is a projective $A[U(k)]$-module. This is true as $|U(k)|$ is invertible in $W(\mathbb {F})$.

Theorem 3.10 The representation $\Gamma _{G, E}$ is multiplicity-free, and

\[ \Gamma_{G, E} \cong \bigoplus_{[s]} \pi_{G}(s) \]

where $[s]$ runs over the $q$-power stable $W$-orbits of $\operatorname {Hom}(I_t, \hat {G}(E))$.

Proof. This is [DL76, Theorem 10.7(ii)].

The final lemma of this section is only needed to compare this paper with [Sho18].

Lemma 3.11 Suppose that $G$ is a product of general linear groups over $\mathcal {O}_F$, that $\tau : I_t \to \hat {G}(E)$ is as in Definition 3.7 and that $\rho : W_t \rightarrow \hat {G}(\overline {E})$ extends $\tau$. Write $K(1) = \ker (G(\mathcal {O}_F) \rightarrow G(k))$. Let $\Pi (\rho )$ be the representation of $G(F)$ associated to $\rho$ by the local Langlands correspondence,² and assume that $\Pi (\rho )$ is generic. Then, as $G(k)$-representations,

\[ \Pi(\rho)^{K(1)} = \pi_G(\tau). \]

Proof. We immediately reduce to the case $G = {\rm GL}_n$. If $\hat {L}$ and $L$ are as in Definition 3.7, and $L/\mathcal {O}_F$ is a Levi subgroup of $G/\mathcal {O}_F$ extending $L/k$, then for any $\rho$ as in the lemma we can conjugate $\rho$ to have image in $\hat {L}(\overline {E})$. We then have

\[ \Pi(\rho) = \operatorname{Ind}_{P(F)}^{G(F)} \Pi_L(\rho) \]

where $\Pi _L$ is the local Langlands correspondence for $L$ and $P$ is a parabolic subgroup with Levi $L$. Taking $K(1)$-invariants, we see that it suffices to prove the lemma in the case that $\tau$ is discrete.

Let $M/\mathcal {O}_F$ be a split Levi subgroup, with dual $\hat {M}$, such that the semisimple part of $\tau$ factors through a discrete parameter $s : I_t \rightarrow \hat {M}(E)$. Then there is $w_0 \in W_M\subset W$ such that $w_0s = s^{q}$, and associated to the pair $(w_0, s)$ we have a representation $\epsilon (w_0)R_M(w_0, s)$ of $M(k)$ which will be cuspidal by [DL76, Theorem 8.3]. We claim that $\pi _G(s)$ is the (unique) nondegenerate irreducible representation of $G(k)$ with cuspidal support given by the pair $(M(k), \epsilon (w_0)R(w_0, s))$. Since $\pi _G(s)$ is nondegenerate by Theorem 3.10, it suffices to show that it has the given cuspidal support. If $M \subset P$ is a parabolic subgroup defined over $k$, then

\[ \operatorname{Ind}_{M(k)}^{G(k)} R_M(w_0, s) = R(w_0, s) \]

by [DL76, Proposition 8.2], where $w_0$ is regarded as an element of both $W_M$ and $W$. We have to show that

\[ \big\langle \pi_G(s), \epsilon(w_0)R(w_0, s) \big\rangle \neq 0. \]

But, by [DL76, Theorem 6.8], we have

\begin{align*} \big\langle \pi_G(s), \epsilon(w_0)R(w_0, s) \big\rangle &= \frac{\epsilon(w_0)}{|W(s)|}\sum_{w \in W(s,s^{q})} \epsilon(w) \big\langle R(w,s), R(w_0, s) \big\rangle\\ &= \frac{\epsilon(w_0)}{|W(s)|} \sum_{w \in W(s, s^{q})}\epsilon(w) |\{x \in W(s) : xwx^{-1} = w_0\}| \\ &= \frac{\epsilon(w_0)}{|W(s)|} \sum_{x \in W(s)} \epsilon(xw_0x^{-1}) \\ &= 1 \end{align*}

as required. Now, the semisimplification of $\rho$ has the form $\rho _M$ for some $\rho _M : W_t \rightarrow \hat {M}(F)$ with $\rho _M|_{I_t} = s$. Then $\Pi (\rho )$ will be a discrete series representation with supercuspidal support $(M, \nu )$ for some supercuspidal representation $\nu = \Pi _M(\rho _M)$. It follows from [Sho18, Corollary 6.21, parts (1) and (2)] that $\Pi (\rho )^{K(1)}$ is the unique nondegenerate irreducible representation of $G(k)$ with cuspidal support $(M(k), \nu ^{K(1) \cap M})$, and we have to show that $\nu ^{K(1) \cap M} = \epsilon (w_0)R(w_0,s)$. Thus we have reduced to the cuspidal case, which boils down to comparing the construction of [DR09] with the known local Langlands correspondence for general linear groups. This is implicit in the remarks following [Yos10, Theorem 1.1]: we spell out the argument.

We may suppose that $M = {\rm GL}_n$ and $s : I_t \rightarrow \hat {T}(E)$ is a semisimple parameter. Then

\[ s \cong \chi \oplus \chi^{\phi} \oplus \dots \oplus \chi^{\phi^{n-1}} \]

for some $\chi : I_t \rightarrow \hat {T}(E)$, where $\chi ^{\phi }$ is the twist of $\chi$ by $\phi \in W_t$, and $w_0 = (12\ldots n) \in W_M \cong S_n$. Let $W'_t$ be the tame Weil group of the unramified extension $F_n/F$ of degree $n$. Then $\chi$ extends to a character $\tilde {\chi }$ of $W'_t$ and $s = \big (\operatorname {Ind}_{W'_t}^{W_t}\tilde {\chi }\big )|_{I_t}$. By [HT01, Lemma 12.7, part (6)],

\[ \Pi\big(\operatorname{Ind}_{W'_t}^{W_t}\tilde{\chi}\big) = \operatorname{Ind}_{F_n}^{F}(\Pi(\tilde{\chi})). \]

Here $\operatorname {Ind}_{F_n}^{F}$ denotes the cyclic automorphic induction of [HH95], which in this case agrees with the construction of [Hen92]. We have that $\Pi (\tilde {\chi })|_{\mathcal {O}_{F_n}}^{\times }$ is inflated from the character $\theta$ of $k_n^{\times }$ corresponding to $\chi$ via the canonical surjection $I_t \twoheadrightarrow k_n^{\times }$. If we take $T \subset M$ to be a maximal torus of type $w_0$, then there is an isomorphism $T(k) \cong k_n^{\times }$. It follows from the main theorem and paragraph 3.4 of [Hen92] that $\big (\operatorname {Ind}_{F_n}^{F}(\Pi (\tilde {\chi }))\big )^{K(1)}$ is, as a representation of $K/K(1) = G(k)$, precisely $(-1)^{n-1}R^{\theta }_T = \epsilon (w_0)R(w_0, s)$, as required.

3.3 Endomorphisms of Gelfand–Graev representations

Notice that the $q$-power stable $W$-orbits of $\operatorname {Hom}(I_t, \hat {G}(E))$ are exactly the $E$-points of the affine scheme $\mathcal {S}^{\hat {G}}(q)$ introduced previously. We write $B_{q,\hat {G}}$ for its ring of functions.

Proposition 3.12 There are canonical isomorphisms

\[ \operatorname{End}_{G(k)}(\Gamma_{G,E}) \cong \prod_{[s]} E \cong B_{q,\hat{G}}\otimes E \]

where $[s]$ runs over the $q$-power stable $W$-orbits of $\operatorname {Hom}(I_t, \hat {G}(E))$.

Proof. The first isomorphism is the product of the ‘Curtis homomorphisms’

\[ \operatorname{End}_{G(k)}(\Gamma_{G,E}) \rightarrow \operatorname{End}_E(\pi_{G}(s)) = E. \]

The second takes the copy of $E$ labelled by $[s]$ to the copy of $E$ corresponding to the point $s$ of $\mathcal {S}_{\hat {G}}(q)$.

Remark 3.13 The problem of determining the integral endomorphism ring $\operatorname {End}_{G(k)}(\Gamma _G)$ (for general connected reductive groups $G$) was considered by Bonnafé and Kessar [BK08], who obtained a description (not involving $B_{q,\hat {G}}$) when $l \nmid |W|$. In the case $G = {\rm GL}_n$, it is in fact true that the map $B_{q,\hat {G}} \rightarrow \operatorname {End}_{G(k)}(\Gamma _G) \otimes E$ that we have obtained restricts to an integral isomorphism of $B_{q,\hat {G}}$ onto $\operatorname {End}_{G(k)}(\Gamma _G)$. This is proved in [Hel20, HM18] as a byproduct of their proof of the local Langlands correspondence in families.³

An elementary proof (that is, one not involving the $p$-adic group $G(F)$) of this integral isomorphism has been found by Li [Li21] when $l > n$, and in fact he proves an analogous result for $G$ any connected reductive group with connected centre. A third ring plays an important role: the Grothendieck ring of mod $p$ representations of $G^{*}(k)$, where $G^{*}$ is the Deligne–Lusztig dual of $G$.

If $L \subset G$ is a Levi subgroup and $s : I_t \to \hat {L}(E)$ is a semisimple parameter, let $\tau _{\hat {L}}(s) : I_t \rightarrow \hat {L}(E)$ be a discrete inertial parameter with semisimple part $s$. Its isomorphism class depends only on the $W_L$ conjugacy class $[s]$ of $s$.

Proposition 3.14 Let $L \subset G$ be a Levi subgroup. Regard $\operatorname {Ind}_{L(k)}^{G(k)}(\Gamma _{L,E})$ as a module over $B_{q,\hat {L}}$ via the homomorphism

\[ B_{q,\hat{L}} \rightarrow B_{q,\hat{L}} \otimes E \xrightarrow{\sim} \operatorname{End}(\Gamma_{L,E}) \rightarrow \operatorname{End}\big(\operatorname{Ind}_{L(k)}^{G(k)}(\Gamma_{L,E})\big). \]

Then, for each $[s] \in \mathcal {S}^{\hat {L}}(q)(E)$, we have an isomorphism of $G(k)$-representations

\[ \operatorname{Ind}_{L(k)}^{G(k)}(\Gamma_{L,E}) \otimes_{B_{q, \hat{L}}, [s]} E \cong \pi_G(\tau_{\hat{L}}(s)). \]

Proof. By the definition of $\pi _G(\tau )$, this immediately reduces to the case $L = G$, in which case it follows from the definition of the isomorphism $B_{q,\hat {G}} \rightarrow \operatorname {End}_{G(k)}(\Gamma _{L,E})$ via Curtis homomorphisms.

3.4 Blocks and localization

Let $\overline {s}$ be an $\mathbb {F}$-point of $\mathcal {S}^{\hat {G}}(q)$, that is, a $q$-power stable semisimple conjugacy class in $\operatorname {Hom}(I_t, \hat {G}(\mathbb {F}))$. Then [BM89, Theorem 2.2] implies that the set of isomorphism classes of irreducible representations that occur in some $R(w,s)$ is a union of blocks for $\mathcal {O}[G(k)]$. In particular, there is a central idempotent $e_{\overline {s}} \in \mathcal {O}[G(k)]$ which acts as the identity on these irreducible representations and as zero on the others.

Let $B_{q,\hat {G}, \overline {s}}$ be the localization of $B_{q,\hat {G}}$ at $\overline {s}$, and consider the projective $\mathcal {O}[G(k)]$-module $e_{\overline {s}}\Gamma _G$ (a direct summand of $\Gamma _G$). Then, again via the product of Curtis homomorphisms, we have a homomorphism

\[ B_{q, \hat{G}, \overline{s}} \rightarrow \operatorname{End}(e_{\overline{s}}\Gamma_{G,E}). \]

Similarly, if $L \subset G$ is a Levi subgroup we have a map

\[ B_{q, \hat{L}, \overline{s}} \rightarrow \operatorname{End}(\operatorname{Ind}_{L(k)}^{G(k)}e_{\overline{s}}\Gamma_{L,E}) \]

and we obtain a corresponding version of Proposition 3.14.

4. The Breuil–Mézard conjecture

If $X$ is any finite-dimensional scheme, let $\mathcal {Z}(X)$ be the free abelian group on the irreducible components of $X$ of maximal dimension. If $X = \operatorname {Spf} A$ for $A \in \mathcal {C}_\mathcal {O}^{\wedge }$, then we write $\mathcal {Z}(X) = \mathcal {Z}(\operatorname {Spec}(A))$.

Let $G$ and $\hat {G}$ be as in § 3, and suppose that $(E,\mathcal {O}, \mathbb {F})$ is sufficiently large in the sense of assumption (3). Define a map

\[ \operatorname{cyc} : K_E(G(k)) \rightarrow \mathcal{Z}(\mathfrak{X}^{\hat{G}}(q)) \]

as follows. By Proposition 2.6, for each isomorphism class of inertial $\hat {G}$-parameter $\tau : I_t \rightarrow \hat {G}(E)$, there is an irreducible (in fact, geometrically irreducible) component $\mathfrak {X}^{\hat {G}}(q, \tau )$ of $\mathfrak {X}^{\hat {G}}(q)$ such that $\rho _x|I_t\cong \tau$ for a Zariski dense (open) set of $x \in \mathfrak {X}^{\hat {G}}(q, \tau )(\overline {E})$. Then for $\sigma$ an irreducible $E$-representation of $G(k)$ we define

\[ \operatorname{cyc}(\sigma) = \sum_{\tau} m(\sigma,\tau)[\mathfrak{X}^{\hat{G}}(q, \tau)], \]

where $m(\sigma, \tau ) = \dim \operatorname {Hom}_{G(k)}(\pi _G(\tau ),\sigma )$, and we extend this linearly to $K_E(G(k))$.

Remark 4.1 It follows from Lemma 3.11 that $\operatorname {cyc}(\sigma ) = \operatorname {cyc}'(\sigma ^{*})$, where $\operatorname {cyc}'$ is the cycle map defined in [Sho18, 4.2] and $\sigma ^{*}$ is the dual of $\sigma$. The dual makes no difference to the following result.

There are reduction maps $\operatorname {red} : K_E(G(k)) \rightarrow K_{\mathbb {F}}(G(k))$ and $\operatorname {red} : \mathcal {Z}(\mathfrak {X}^{\hat {G}}(q)) \rightarrow \mathcal {Z}(\mathfrak {X}^{\hat {G}}(q)_{\mathbb {F}})$, the first defined by choosing a lattice, applying $\otimes _\mathcal {O} \mathbb {F}$, and taking the image in the Grothendieck group, and the second defined by intersection with the special fibre, as in [Sho18, § 2.3].

Theorem 4.2 There exists a homomorphism $\overline {\operatorname {cyc}} : K_{\mathbb {F}}(G(k)) \rightarrow \mathcal {Z}(\mathfrak {X}^{\hat {G}}(q)_{\mathbb {F}})$ such that the diagram

(15)

commutes.

Proof. Let $f$ be an integer large enough for $\hat {G}$ (see Definition 2.15). By [Sho18, Lemma 2.10], it is enough prove the theorem after enlarging $\mathcal {O}$. Then, by [Sho18, Proposition 7.1] and Lemma 2.17, it suffices to prove the theorem with $\mathfrak {X}^{\hat {G}}(q)$ replaced by $X_{\overline {\rho }}^{\hat {G}}$ for $\overline {\rho }$ an $f$-distinguished $\mathbb {F}$-point of $\mathfrak {X}^{\hat {G}}(q)$. (The idea is that, for each point $\overline {\rho } \in \mathfrak {X}^{\hat {G}}(q)$, the natural homomorphism

\[ \mathcal{Z}(\mathfrak{X}^{\hat{G}}(q)) \to \mathcal{Z}(X^{\hat{G}}_{\overline{\rho}}) \]

commutes with the cycle map and with reduction modulo $l$. To get the result for $\mathfrak {X}^{\hat {G}}(q)$ it is then enough to consider $X^{\hat {G}}_{\overline {\rho }}$ for a $\overline {\rho }$ on each irreducible component.) Let $\overline {\rho }$ be such an $f$-distinguished point and let $\hat {L}$ be an $f$-allowable Levi subgroup for $\overline {\rho }$. By Theorem 2.16, there is a formally smooth morphism

\[ X_{\overline{\rho}}^{\hat{G}} \rightarrow S_{\overline{s}}^{\hat{L}}. \]

We have that $S_{\overline {s}}^{\hat {L}} = \operatorname {Spec} B_{q, \hat {L}, \overline {s}}$ and that $B_{q, \hat {L}, \overline {s}}$ is a finite flat local $\mathcal {O}$-algebra.

It follows from this that $\mathcal {Z}(X_{\overline {\rho }}^{\hat {G}} \otimes \mathbb {F}) \cong \mathbb {Z}$ is generated by the class of the unique irreducible component, and $\mathcal {Z}(\mathfrak {X}^{\hat {G}})$ is the free abelian group on the $E$-points $[s]$ of $S_{\overline {s}}^{\hat {L}}$. With these identifications, by Theorem 2.16 the reduction map on the right is simply

\[ \sum a_{[s]} [s] \mapsto \sum a_{[s]}, \]

and we seek a map $\overline {\operatorname {cyc}} : K_{\mathbb {F}}(G(k)) \rightarrow \mathbb {Z}$ such that

\[ \overline{\operatorname{cyc}}(\overline{\sigma}) = \sum_{[s]} m(\sigma,\tau_{\hat{L}}(s)) \]

for all $\sigma \in K_E(G(k))$.

Let $\Theta = \operatorname {Ind}_{L(k)}^{G(k)} e_{\overline {s}}\Gamma _L$. Then $\Theta$ is a finitely generated projective $\mathcal {O}[G(k)]$-module by Lemma 3.9, the fact that $e_{\overline {s}}$ is an idempotent, and the fact that $\operatorname {Ind}$ takes projectives to projectives. If $\Theta _E = \Theta \otimes E$ then we have a homomorphism

\[ B_{q,\hat{L},\overline{s}} \rightarrow \operatorname{End}_{G(k)}(\Theta_E) \]

from §§ 3.3 and 3.4. For any $\mathcal {O}[G(k)]$-representation $\sigma$, define $\Theta (\sigma )$ to be $\operatorname {Hom}_{\mathcal {O}[G(k)]}(\Theta, \sigma )$, an exact functor of $\sigma$. I claim that $\overline {\operatorname {cyc}}$ can be defined by setting

\[ \overline{\operatorname{cyc}}(\nu) = \dim_\mathbb{F} \Theta(\nu) \]

for irreducible representations $\nu$ of $G(k)$ over $\mathbb {F}$, and extending linearly. Note that, since $\Theta (\cdot )$ is exact, if $\omega$ is any representation of $G(k)$ over $\mathbb {F}$ with image $[\omega ]$ in $K_\mathbb {F}(G(k))$, then

\[ \overline{\operatorname{cyc}}([\omega]) = \dim_\mathbb{F} \Theta(\omega). \]

Now, for $\sigma$ an irreducible $E$-representation of $G(k)$ admitting a lattice $\sigma ^{\circ }$, the projectivity of $\Theta$ gives that the natural map

(16)\begin{equation} \operatorname{Hom}_{\mathcal{O}[G(k)]}(\Theta, \sigma^{\circ})\otimes_{\mathcal{O}} \mathbb{F} \to \operatorname{Hom}_{\mathcal{O}[G(k)]}(\Theta, \overline{\sigma})\end{equation}

is an isomorphism. Therefore

\begin{align*} \sum_{[s]} m(\sigma, \tau_{\hat{L}}(s)) &= \sum_{[s]} \dim \operatorname{Hom}_{E[G(k)]}(\Theta_E \otimes_{B_{q,\hat{G}, \overline{s}}, [s]} E, \sigma) \\ \textrm{(by Proposition 3.14 and the discussion of {\$} 3.4)} &= \dim_E \Theta(\sigma) \\ &= \operatorname{rank}_\mathcal{O} \Theta(\sigma^{\circ})\\ &= \dim_\mathbb{F}\Theta(\overline{\sigma})\\ \textrm{(by the isomorphism (16))} &= \overline{\operatorname{cyc}}(\overline{\sigma}) \end{align*}

as required. The theorem follows.

Remark 4.3 Theorem 4.2 falls slightly short of the Breuil–Mézard conjecture as formulated in [Sho18] since, in effect, only representations of $G(\mathcal {O}_F)$ with $K(1)$-fixed vectors are considered. It may be possible to adapt our methods to deal with all representations of $G(\mathcal {O}_F)$, perhaps by using the Gelfand–Graev representation to construct a projective representation of $G(\mathcal {O}_F)$ that interpolates the restrictions to $G(\mathcal {O}_F)$ of the various generic irreducible admissible depth-zero representations of $G(F)$. However, we have not yet been able to carry this out.