In  $\mathsf {ZF}$ (i.e., Zermelo–Fraenkel set theory minus the axiom of choice (
$\mathsf {ZF}$ (i.e., Zermelo–Fraenkel set theory minus the axiom of choice (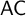 $\mathsf {AC}$)), we investigate the open problem of the deductive strength of the principle
$\mathsf {AC}$)), we investigate the open problem of the deductive strength of the principle
UFwob(ω): “There exists a free ultrafilter on ω with a well-orderable base”,
which was introduced by Herzberg, Kanovei, Katz, and Lyubetsky [(2018), Journal of Symbolic Logic, 83(1), 385–391]. Typical results are:
(1) “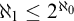 $\aleph _{1}\leq 2^{\aleph _{0}}$” is strictly weaker than
$\aleph _{1}\leq 2^{\aleph _{0}}$” is strictly weaker than 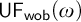 $\mathsf {UF_{wob}}(\omega )$ in
$\mathsf {UF_{wob}}(\omega )$ in  $\mathsf {ZF}$.
$\mathsf {ZF}$.
(2) “There exists a free ultrafilter on 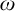 $\omega $” does not imply “
$\omega $” does not imply “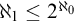 $\aleph _{1}\leq 2^{\aleph _{0}}$” in
$\aleph _{1}\leq 2^{\aleph _{0}}$” in  $\mathsf {ZF}$, and thus (by (1)) neither does it imply
$\mathsf {ZF}$, and thus (by (1)) neither does it imply  $\mathsf {UF_{wob}}(\omega )$ in
$\mathsf {UF_{wob}}(\omega )$ in  $\mathsf {ZF}$. This fills the gap in information in Howard and Rubin [Mathematical Surveys and Monographs, American Mathematical Society, 1998], as well as in Herzberg et al. (2018).
$\mathsf {ZF}$. This fills the gap in information in Howard and Rubin [Mathematical Surveys and Monographs, American Mathematical Society, 1998], as well as in Herzberg et al. (2018).
(3) Martin’s Axiom (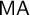 $\mathsf {MA}$) implies “no free ultrafilter on
$\mathsf {MA}$) implies “no free ultrafilter on 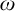 $\omega $ has a well-orderable base of cardinality
$\omega $ has a well-orderable base of cardinality 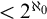 $<2^{\aleph _{0}}$”, and the latter principle is not implied by
$<2^{\aleph _{0}}$”, and the latter principle is not implied by 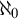 $\aleph _{0}$-Martin’s Axiom (
$\aleph _{0}$-Martin’s Axiom (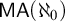 $\mathsf {MA}(\aleph _{0})$) in
$\mathsf {MA}(\aleph _{0})$) in  $\mathsf {ZF}$.
$\mathsf {ZF}$.
(4)  $\mathsf {MA} + \mathsf {UF_{wob}}(\omega )$ implies
$\mathsf {MA} + \mathsf {UF_{wob}}(\omega )$ implies 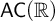 $\mathsf {AC}(\mathbb {R})$ (the axiom of choice for non-empty sets of reals), which in turn implies
$\mathsf {AC}(\mathbb {R})$ (the axiom of choice for non-empty sets of reals), which in turn implies  $\mathsf {UF_{wob}}(\omega )$. Furthermore,
$\mathsf {UF_{wob}}(\omega )$. Furthermore, 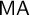 $\mathsf {MA}$ and
$\mathsf {MA}$ and  $\mathsf {UF_{wob}}(\omega )$ are mutually independent in
$\mathsf {UF_{wob}}(\omega )$ are mutually independent in  $\mathsf {ZF}$.
$\mathsf {ZF}$.
(5) For any infinite linearly orderable set X, each of “every filter base on X can be well ordered” and “every filter on X has a well-orderable base” is equivalent to “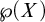 $\wp (X)$ can be well ordered”. This yields novel characterizations of the principle “every linearly ordered set can be well ordered” in
$\wp (X)$ can be well ordered”. This yields novel characterizations of the principle “every linearly ordered set can be well ordered” in 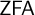 $\mathsf {ZFA}$ (i.e., Zermelo–Fraenkel set theory with atoms), and of
$\mathsf {ZFA}$ (i.e., Zermelo–Fraenkel set theory with atoms), and of 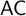 $\mathsf {AC}$ in
$\mathsf {AC}$ in  $\mathsf {ZF}$.
$\mathsf {ZF}$.
(6) “Every filter on 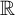 $\mathbb {R}$ has a well-orderable base” implies “every filter on
$\mathbb {R}$ has a well-orderable base” implies “every filter on 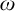 $\omega $ has a well-orderable base”, which in turn implies
$\omega $ has a well-orderable base”, which in turn implies  $\mathsf {UF_{wob}}(\omega )$, and none of these implications are reversible in
$\mathsf {UF_{wob}}(\omega )$, and none of these implications are reversible in  $\mathsf {ZF}$.
$\mathsf {ZF}$.
(7) “Every filter on 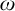 $\omega $ can be extended to an ultrafilter with a well-orderable base” is equivalent to
$\omega $ can be extended to an ultrafilter with a well-orderable base” is equivalent to 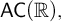 $\mathsf {AC}(\mathbb {R}),$ and thus is strictly stronger than
$\mathsf {AC}(\mathbb {R}),$ and thus is strictly stronger than  $\mathsf {UF_{wob}}(\omega )$ in
$\mathsf {UF_{wob}}(\omega )$ in  $\mathsf {ZF}$.
$\mathsf {ZF}$.
(8) “Every filter on 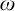 $\omega $ can be extended to an ultrafilter” implies “there exists a free ultrafilter on
$\omega $ can be extended to an ultrafilter” implies “there exists a free ultrafilter on 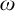 $\omega $ which has no well-orderable base of cardinality
$\omega $ which has no well-orderable base of cardinality 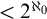 ${<2^{\aleph _{0}}}$”. The former principle does not imply “there exists a free ultrafilter on
${<2^{\aleph _{0}}}$”. The former principle does not imply “there exists a free ultrafilter on 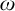 $\omega $ which has no well-orderable base” in
$\omega $ which has no well-orderable base” in  $\mathsf {ZF}$, and the latter principle is true in the Basic Cohen Model.
$\mathsf {ZF}$, and the latter principle is true in the Basic Cohen Model.
 $\omega $ WITH WELL-ORDERABLE BASES IN
$\omega $ WITH WELL-ORDERABLE BASES IN  $\mathsf {ZF}$
$\mathsf {ZF}$