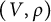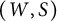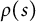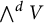Let W be a group endowed with a finite set S of generators. A representation $(V,\rho )$ of W is called a reflection representation of $(W,S)$ if $\rho (s)$ is a (generalized) reflection on V for each generator $s \in S$. In this article, we prove that for any irreducible reflection representation V, all the exterior powers $\bigwedge ^d V$, $d = 0, 1, \dots , \dim V$, are irreducible W-modules, and they are non-isomorphic to each other. This extends a theorem of R. Steinberg which is stated for Euclidean reflection groups. Moreover, we prove that the exterior powers (except for the 0th and the highest power) of two non-isomorphic reflection representations always give non-isomorphic W-modules. This allows us to construct numerous pairwise non-isomorphic irreducible representations for such groups, especially for Coxeter groups.

In 1968, Steinberg [Endomorphisms of Linear Algebraic Groups, Memoirs of the American Mathematical Society, 80 (American Mathematical Society, Providence, RI, 1968)] proved a theorem stating that the exterior powers of an irreducible reflection representation of a Euclidean reflection group are again irreducible and pairwise nonisomorphic. We extend this result to a more general context where the inner product invariant under the group action may not necessarily exist.

Let U be an n -dimensional vector space over a finite field of q elements. The number of elements of Λ2U of each irreducible length is found using the isomorphism of Λ2U with Hn, the space of n x n skew-symmetric matrices, and results due to Carlitz and MacWilliams on the number of skew-symmetric matrices of any given rank.