Hostname: page-component-f554764f5-246sw Total loading time: 0 Render date: 2025-04-14T06:49:01.445Z Has data issue: false hasContentIssue false
  • English
  • Français

On exterior powers of reflection representations, II

Part of: Metric geometry Basic linear algebra Representation theory of groups Special aspects of infinite or finite groups Algebraic combinatorics

Published online by Cambridge University Press:  24 March 2025

Hongsheng Hu Open the ORCID record for Hongsheng Hu [Opens in a new window]
Hongsheng Hu*
Affiliation:
School of Mathematics, Hunan University, Changsha 410082, China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let W be a group endowed with a finite set S of generators. A representation 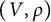$(V,\rho )$ of W is called a reflection representation of 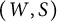$(W,S)$ if 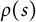$\rho (s)$ is a (generalized) reflection on V for each generator $s \in S$. In this article, we prove that for any irreducible reflection representation V, all the exterior powers 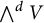$\bigwedge ^d V$, $d = 0, 1, \dots , \dim V$, are irreducible W-modules, and they are non-isomorphic to each other. This extends a theorem of R. Steinberg which is stated for Euclidean reflection groups. Moreover, we prove that the exterior powers (except for the 0th and the highest power) of two non-isomorphic reflection representations always give non-isomorphic W-modules. This allows us to construct numerous pairwise non-isomorphic irreducible representations for such groups, especially for Coxeter groups.

Keywords

Exterior powersgeneralized reflectionsreflection representationsCoxeter groups

MSC classification

Primary: 15A75: Exterior algebra, Grassmann algebras
Secondary: 05E10: Combinatorial aspects of representation theory 20C15: Ordinary representations and characters 20F55: Reflection and Coxeter groups 51F15: Reflection groups, reflection geometries
Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 23
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bourbaki, N., Lie groups and lie algebras. Chapters 4–6, Elements of Mathematics, Springer-Verlag, Berlin, 2002. Translated from the 1968 French original by Andrew Pressley.Google Scholar
Curtis, C. W., Iwahori, N., and Kilmoyer, R. W., Hecke algebras and characters of parabolic type of finite groups with $\left(B,N\right)$ -pairs . Inst. Hautes Études Sci. Publ. Math. 40(1971), 81–116.Google Scholar
Fulton, W. and Harris, J., Representation theory. A first course, volume 129 of Graduate Texts in Mathematics, Springer-Verlag, New York, NY, 1991.Google Scholar
Geck, M. and Pfeiffer, G., Characters of finite coxeter groups and Iwahori-Hecke algebras, volume 21 of London Mathematical Society Monographs. New Series, The Clarendon Press, Oxford University Press, New York, NY, 2000.Google Scholar
Henderson, A., Exterior powers of the reflection representation in the cohomology of Springer fibres . C. R. Math. Acad. Sci. Paris 348(2010), nos. 19–20, 1055–1058.Google Scholar
Hu, H., On exterior powers of reflection representations . Bull. Aust. Math. Soc. 110(2024), no. 1, 90–102.Google Scholar
Hu, H., Reflection representations of Coxeter groups and homology of Coxeter graphs . Algebr. Represent. Theory 27(2024), no. 1, 961–994.Google Scholar
Sommers, E., Exterior powers of the reflection representation in Springer theory . Transform. Groups 16(2011), no. 3, 889–911.Google Scholar
Steinberg, R., Endomorphisms of linear algebraic groups, volume 80 of Memoirs of the American Mathematical Society, American Mathematical Society, Providence, RI, 1968.Google Scholar