We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We show that for a Noetherian ring A that is I-adically complete for an ideal I, if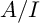 
$A/I$ admits a dualizing complex, so does A. This gives an alternative proof of the fact that a Noetherian complete local ring admits a dualizing complex. We discuss several consequences of this result. We also consider a generalization of the notion of dualizing complexes to infinite-dimensional rings and prove the results in this generality. In addition, we give an alternative proof of the fact that every excellent Henselian local ring admits a dualizing complex, using ultrapower.
