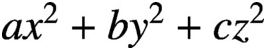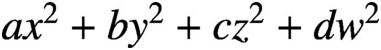2 results
PRIME-UNIVERSAL DIAGONAL QUADRATIC FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 390-404
- Print publication:
- June 2021
-
- Article
- Export citation
Small Solutions of ϕ1x12 + . . . + ϕnxn2 = 0
-
- Journal:
- Canadian Journal of Mathematics / Volume 52 / Issue 3 / 01 June 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 613-632
- Print publication:
- 01 June 2000
-
- Article
-
- You have access
- Export citation