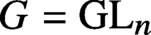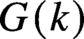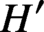1 results
Semisimplification for subgroups of reductive algebraic groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 09 November 2020, e43
-
- Article
-
- You have access
- Open access
- Export citation