Hostname: page-component-6bf8c574d5-qdpjg Total loading time: 0 Render date: 2025-02-25T19:44:57.937Z Has data issue: false hasContentIssue false
  • English
  • Français

Semisimplification for subgroups of reductive algebraic groups

Part of: Algebraic groups Linear algebraic groups and related topics

Published online by Cambridge University Press:  09 November 2020

Michael Bate ,
Benjamin Martin  and
Gerhard Röhrle
Michael Bate
Affiliation:
Department of Mathematics, University of York, YorkYO10 5DD, United Kingdom; E-mail: [email protected]
Benjamin Martin
Affiliation:
Department of Mathematics, University of Aberdeen, King’s College, Fraser Noble Building, AberdeenAB24 3UE, United Kingdom; E-mail: [email protected]
Gerhard Röhrle
Affiliation:
Fakultät für Mathematik, Ruhr-Universität Bochum, Universitätsstraße 150, D-44780Bochum, Germany; E-mail: [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

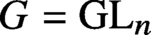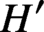Let G be a reductive algebraic group—possibly non-connected—over a field k, and let H be a subgroup of G. If $G= {GL }_n$ , then there is a degeneration process for obtaining from H a completely reducible subgroup $H'$ of G; one takes a limit of H along a cocharacter of G in an appropriate sense. We generalise this idea to arbitrary reductive G using the notion of G-complete reducibility and results from geometric invariant theory over non-algebraically closed fields due to the authors and Herpel. 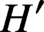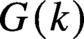Our construction produces a G-completely reducible subgroup $H'$ of G, unique up to $G(k)$ -conjugacy, which we call a k-semisimplification of H. This gives a single unifying construction that extends various special cases in the literature (in particular, it agrees with the usual notion for 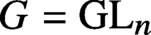$G= GL _n$ and with Serre’s ‘G-analogue’ of semisimplification for subgroups of 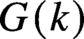$G(k)$ from [19]). We also show that under some extra hypotheses, one can pick 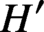$H'$ in a more canonical way using the Tits Centre Conjecture for spherical buildings and/or the theory of optimal destabilising cocharacters introduced by Hesselink, Kempf, and Rousseau.

Keywords

semisimplificationG-complete reducibilitygeometric invariant theoryrationalitycocharacter-closed orbitsdegeneration of G-orbits

MSC classification

Primary: 20G15: Linear algebraic groups over arbitrary fields
Secondary: 14L24: Geometric invariant theory
Type
Algebra
Information
Forum of Mathematics, Sigma , Volume 8 , 2020 , e43
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2020. Published by Cambridge University Press

References

Bate, M., Herpel, S., Martin, B., and Röhrle, G., ‘Cocharacter-closure and the rational Hilbert-Mumford theorem’, Math. Z. 287(1–2) (2017), 39–72.CrossRefGoogle Scholar
Bate, M., Martin, B., and Röhrle, G., ‘A geometric approach to complete reducibility’, Invent. Math. 161(1) (2005), 177–218.CrossRefGoogle Scholar
Bate, M., Martin, B., and Röhrle, G., ‘Complete reducibility and separable field extensions’, C. R. Acad. Sci. Paris Ser. I Math. 348 (2010), 495–497.10.1016/j.crma.2010.04.013CrossRefGoogle Scholar
Bate, M., Martin, B., and Röhrle, G., ‘The strong centre conjecture: an invariant theory approach’, J. Algebra 372 (2012), 505–530.CrossRefGoogle Scholar
Bate, M., Martin, B., Röhrle, G., and Tange, R., ‘Complete reducibility and separability’, Trans. Amer. Math. Soc. 362(8) (2010), 4283–4311.CrossRefGoogle Scholar
Bate, M., Martin, B., Röhrle, G., and Tange, R., ‘Closed orbits and uniform $S$ -instability in geometric invariant theory’, Trans. Amer. Math. Soc. 365(7) (2013), 3643–3673.CrossRefGoogle Scholar
Borel, A., ‘Linear algebraic groups’, Graduate Texts in Mathematics 126 (Springer-Verlag, 1991).Google Scholar
Brüstle, T., Hille, L., Röhrle, G., and Zwara, G., ‘The Bruhat-Chevalley order of parabolic group actions in general linear groups and degeneration for $\Delta$ -filtered modules’, Adv. Math. 148(2) (1999), 203–242.CrossRefGoogle Scholar
Herpel, S. and Stewart, D.I., ‘On the smoothness of normalisers, the subalgebra structure of modular Lie algebras, and the cohomology of small representations’, Doc. Math. 21 (2016), 1–37.Google Scholar
Hesselink, W.H., ‘Uniform instability in reductive groups’, J. Reine Angew. Math. 303/304 (1978), 74–96.Google Scholar
Kempf, G.R., ‘Instability in invariant theory’, Ann. Math. 108 (1978), 299–316.CrossRefGoogle Scholar
Kraft, H., ‘Geometric methods in representation theory’, in Representations of Algebras (Puebla, 1980), 180–258, Lecture Notes in Math. 944, (Springer, Berlin-New York, 1982).Google Scholar
Lawrence, B. and Sawin, W., ‘The Shafarevich conjecture for hypersurfaces in abelian varieties’, preprint (2020), https://arxiv.org/abs/2004.09046.Google Scholar
Lawrence, B. and Venkatesh, A., ‘Diophantine problems and $p$ -adic period mappings’, Invent. Math. 221(2020), no. 3, 893–999.CrossRefGoogle Scholar
Martin, B., ‘Generic stabilisers for actions of reductive groups’, Pacific J. Math. 279 (2015), 397–422.CrossRefGoogle Scholar
Riedtmann, C., ‘Degenerations for representations of quivers with relations’, Ann. Sci. École Norm. Sup. (4) 19 (1986), 275–301.CrossRefGoogle Scholar
Rousseau, G., ‘Immeubles sphériques et théorie des invariants’, C. R. Acad. Sci. Paris Sér. A–B 286(5) (1978), A247–A250.Google Scholar
Serre, J-P., ‘La notion de complète réductibilité dans les immeubles sphériques et les groupes réductifs’, Séminaire au Collège de France, résumé dans [21, pp. 93–98.] (1997).Google Scholar
Serre, J-P., ‘Complète réductibilité’, Séminaire Bourbaki, 56ème année, 2003–2004, n $\!^\mathrm{o}$ 932.Google Scholar
Springer, T.A., Linear Algebraic Groups , 2nd edition, Progress in Mathematics 9 (Birkhäuser Boston, Inc., Boston, MA, 1998).CrossRefGoogle Scholar
Tits, J., ‘Théorie des groupes’, Résumé des Cours et Travaux, Annuaire du Collège de France, 97e année, (1996–1997), 89–102.Google Scholar
Uchiyama, T., ‘Complete reducibility of subgroups of reductive algebraic groups over nonperfect fields I’, J. Algebra 463 (2016), 168–187.CrossRefGoogle Scholar
Zwara, G., ‘Degenerations for modules over representation-finite algebras’, Proc. Amer. Math. Soc. 127 (1999), 1313–1322.CrossRefGoogle Scholar
Zwara, G., ‘Degenerations of finite-dimensional modules are given by extensions’. Compositio Math. 121(2) (2000), 205–218.CrossRefGoogle Scholar