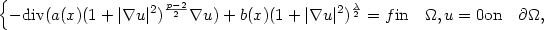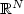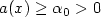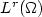1 results
Uniqueness of renormalized solutions to nonlinear elliptic equations with a lower order term and right-hand side in L 1(Ω)
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 8 / 2002
- Published online by Cambridge University Press:
- 15 August 2002, pp. 239-272
- Print publication:
- 2002
-
- Article
- Export citation
-
In this paper we prove uniqueness results for the renormalized solution, if it exists, of a class ofnon coercive nonlinear problems whose prototype is $$\left\{- \hbox{div}( a(x)(1+|\nabla u|^{2})^{\frac{p-2}{2}}\nabla u) +b(x)(1+|\nabla u|^{2})^{\frac{\lambda}{2}} =f\hbox{in}\quad\Omega, u=0\hbox{on} \quad \partial\Omega,\right.$$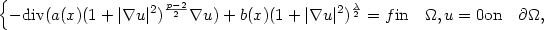
where Ω is a bounded open subset of ${\mathbb{R}}^N$ 
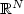, N > 2, 2-1/N < p < N , a belongs to L ∞(Ω), $a(x)\ge\alpha_0>0$ 
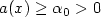,f is a function inL 1(Ω), b is a function in $L^r(\Omega)$ 
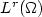and 0 ≤ λ < λ *(N,p,r), for some r and λ *(N,p,r).
