In addition to the features of the two-parameter Chinese restaurant process (CRP), the restaurant under consideration has a cocktail bar and hence allows for a wider range of (bar and table) occupancy mechanisms. The model depends on three real parameters, $\alpha$ , $\theta_1$ , and $\theta_2$ , fulfilling certain conditions. Results known for the two-parameter CRP are carried over to this model. We study the number of customers at the cocktail bar, the number of customers at each table, and the number of occupied tables after n customers have entered the restaurant. For $\alpha>0$ the number of occupied tables, properly scaled, is asymptotically three-parameter Mittag–Leffler distributed as n tends to infinity. We provide representations for the two- and three-parameter Mittag–Leffler distribution leading to efficient random number generators for these distributions. The proofs draw heavily from methods known for exchangeable random partitions, martingale methods known for generalized Pólya urns, and results known for the two-parameter CRP.

We consider a class of discrete-time Markov chains with state space [0, 1] and the following dynamics. At each time step, first the direction of the next transition is chosen at random with probability depending on the current location. Then the length of the jump is chosen independently as a random proportion of the distance to the respective end point of the unit interval, the distributions of the proportions being fixed for each of the two directions. Chains of that kind were the subjects of a number of studies and are of interest for some applications. Under simple broad conditions, we establish the ergodicity of such Markov chains and then derive closed-form expressions for the stationary densities of the chains when the proportions are beta distributed with the first parameter equal to 1. Examples demonstrating the range of stationary distributions for processes described by this model are given, and an application to a robot coverage algorithm is discussed.

Using a characterizing equation for the beta distribution, Stein's method is applied to obtain bounds of the optimal order for the Wasserstein distance between the distribution of the scaled number of white balls drawn from a Pólya-Eggenberger urn and its limiting beta distribution. The bound is computed by making a direct comparison between characterizing operators of the target and the beta distribution, the former derived by extending Stein's density approach to discrete distributions. In addition, refinements are given to Döbler's (2012) result for the arcsine approximation for the fraction of time a simple random walk of even length spends positive, and so also to the distributions of its last return time to 0 and its first visit to its terminal point, by supplying explicit constants to the present Wasserstein bound and also demonstrating that its rate is of the optimal order.

In this paper, we propose a matrix-variate generalization of the Gauss hypergeometric distribution and study several of its properties. We also derive probability density functions of the product of two independent random matrices when one of them is Gauss hypergeometric. These densities are expressed in terms of Appell’s first hypergeometric function F1 and Humbert’s confluent hypergeometric function Φ1of matrix arguments.

In this paper we study different types of planar random motions (performed with constant velocity) with three directions, defined by the vectors dj = (cos(2πj/3), sin(2πj/3)) for j = 0, 1, 2, changing at Poisson-paced times. 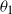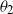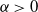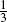We examine the cyclic motion (where the change of direction is deterministic), the completely uniform motion (where at each Poisson event each direction can be taken with probability ) and the symmetrically deviating case (where the particle can choose all directions except that taken before the Poisson event). For each of the above random motions we derive the explicit distribution of the position of the particle, by using an approach based on order statistics. We prove that the densities obtained are solutions of the partial differential equations governing the processes. We are also able to give the explicit distributions on the boundary and, for the case of the symmetrically deviating motion, we can write it as the distribution of a telegraph process. For the symmetrically deviating motion we use a generalization of the Bose-Einstein statistics in order to determine the distribution of the triple (N0, N1, N2) (conditional on N(t) = k, with N0 + N1 + N2 = N(t) + 1, where N(t) is the number of Poisson events in [0, t]), where Nj denotes the number of times the direction dj (j = 0, 1, 2) is taken. Possible extensions to four directions or more are briefly considered.

In this paper, isotropic random projections of d-sets in ℝn are studied, where a d-set is a subset of a d-dimensional affine subspace which satisfies certain regularity conditions. The squared volume reduction induced by the projection of a d-set onto an isotropic random p-subspace is shown to be distributed as a product of independent beta-distributed random variables, for d ≤ p. One of the proofs of this result uses Wilks' lambda distribution from multivariate normal theory. The result is related to Cauchy's and Crofton's formulae in stochastic geometry. In particular, it can be used to give a new and quite simple proof of one of the classical Crofton intersection formulae.

A manpower system of constant size, controlled by recruitment, is described by a partially stochastic model in which there are fixed promotion rates, no demotions and stochastic wastage. The geometric-probabilistic relationship is examined for the attainability after one step and after two steps.

This paper is concerned with the Markovian sequence Xn = Zn max{Xn–1, Yn},n ≧ 1, where X0 is any random variable, {Zn} and {Yn} are independent sequences of i.i.d. random variables both independent of X0. We consider the problem of characterizing the class of stationary distributions arising in such a model and give criteria for a d.f. to belong to it. We develop further results when the Zn's are random variables concentrated on the interval [0, 1], namely having a beta distribution.

The random splitting model of Lloyd and Williams (1988) is generalised, to allow first beta splitting distributions and secondly, discrete splitting distributions. Analogues of some earlier results are developed. In particular, the equality of the average value of the largest split and the probability that this is achieved at the first split continues to hold.

Optimal stopping rules under various conditions are obtained for a proofreader who has a probability p (known or unknown) of detecting a misprint in proofsheets which contain an unknown but Poisson-distributed number of misprints.