11 results
SATISFACTION CLASSES WITH APPROXIMATE DISJUNCTIVE CORRECTNESS
- Part of
-
- Journal:
- The Review of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 13 December 2024, pp. 1-18
-
- Article
-
- You have access
- HTML
- Export citation
11 - Formal Truth
-
- Book:
- The Road to Paradox
- Published online:
- 17 October 2024
- Print publication:
- 31 October 2024, pp 291-354
-
- Chapter
- Export citation

The Road to Paradox
- A Guide to Syntax, Truth and Modality
-
- Published online:
- 17 October 2024
- Print publication:
- 31 October 2024
CLASSICAL DETERMINATE TRUTH I
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 July 2023, pp. 218-261
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AXIOMATIZATIONS OF PEANO ARITHMETIC: A TRUTH-THEORETIC VIEW
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 12 December 2022, pp. 1526-1555
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MODEL THEORY AND PROOF THEORY OF THE GLOBAL REFLECTION PRINCIPLE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 20 May 2022, pp. 738-779
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE MODAL LOGICS OF KRIPKE–FEFERMAN TRUTH
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 27 October 2020, pp. 362-396
- Print publication:
- March 2021
-
- Article
- Export citation
TRUTH AND FEASIBLE REDUCIBILITY
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 20 September 2019, pp. 367-421
- Print publication:
- March 2020
-
- Article
- Export citation
MODELS OF POSITIVE TRUTH
-
- Journal:
- The Review of Symbolic Logic / Volume 12 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 144-172
- Print publication:
- March 2019
-
- Article
- Export citation
TRUTHS, INDUCTIVE DEFINITIONS, AND KRIPKE-PLATEK SYSTEMS OVER SET THEORY
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 23 October 2018, pp. 868-898
- Print publication:
- September 2018
-
- Article
- Export citation
Axiomatizing Kripke's theory of truth
-
- Journal:
- The Journal of Symbolic Logic / Volume 71 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 12 March 2014, pp. 677-712
- Print publication:
- June 2006
-
- Article
- Export citation

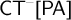
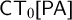
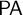
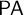





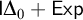
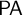


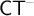

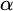


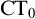
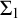
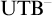
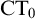
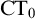
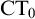

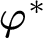

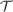
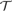
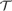
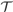
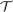
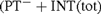
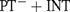
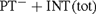
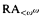 ramified analysis or a system of Tarskian ramified truth up to ω
ramified analysis or a system of Tarskian ramified truth up to ω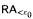 of ramified analysis up to ε
of ramified analysis up to ε