Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-01-13T20:32:33.339Z Has data issue: false hasContentIssue false
  • English
  • Français

TRUTH AND FEASIBLE REDUCIBILITY

Published online by Cambridge University Press:  20 September 2019

ALI ENAYAT ,
MATEUSZ ŁEŁYK  and
BARTOSZ WCISŁO
ALI ENAYAT
Affiliation:
DEPARTMENT OF PHILOSOPHY, LINGUISTICS, AND THEORY OF SCIENCE UNIVERSITY OF GOTHENBURG, BOX 200 405 30 GOTHENBURG, SWEDEN E-mail: [email protected]
MATEUSZ ŁEŁYK
Affiliation:
INSTITUTE OF PHILOSOPHY UNIVERSITY OF WARSAW UL. KRAKOWSKIE PRZEDMIEŚCIE 3 00-927 WARSZAWA, POLAND E-mail: [email protected]
BARTOSZ WCISŁO
Affiliation:
INSTITUTE OF MATHEMATICS, POLISH ACADEMY OF SCIENCES UL. ŚNIADECKICH 8 00-656 WARSZAWA, POLAND E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 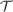${\cal T}$ be any of the three canonical truth theories CT− (compositional truth without extra induction), FS− (Friedman–Sheard truth without extra induction), or KF− (Kripke–Feferman truth without extra induction), where the base theory of 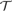${\cal T}$ is PA (Peano arithmetic). We establish the following theorem, which implies that 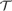${\cal T}$ has no more than polynomial speed-up over PA.

Theorem.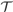${\cal T}$is feasibly reducible to PA, in the sense that there is a polynomial time computable function f such that for every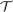${\cal T}$-proof π of an arithmetical sentence ϕ, f (π) is a PA-proof of ϕ.

Keywords

Primary 03F3003C62Secondary 03D1503H15axiomatic theories of truthcompositional truthconservativityfeasible computationspolynomial simulationreducibilityspeed-uptruth predicates
Type
Articles
Information
The Journal of Symbolic Logic , Volume 85 , Issue 1 , March 2020 , pp. 367 - 421
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Caldon, P. and Ignjatović, A., On mathematical instrumentalism, this Journal, vol. 70 (2005), no. 13, pp. 778–794.Google Scholar
Cantini, A., Notes on formal theories of truth. Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 35 (1989), no. 1, pp. 97–130.CrossRefGoogle Scholar
Cieśliński, C., The Epistemic Lightness of Truth: Deflationism and its Logic, Cambridge University Press, Cambridge, 2018.Google Scholar
Cieśliński, C., Łełyk, M., and Wcisło, B., Models of PT− with internal induction for total formulae. The Review of Symbolic Logic, vol. 10 (2017), no. 1, pp. 187–202.CrossRefGoogle Scholar
Enayat, A., Problem 1 in “A list of open problems”. Submitted to the conference Model Theory and Proof Theory of Arithmetic (2012). https://www.impan.pl/∼kz/KR/slides/KR_OpenProblems.pdf.Google Scholar
Enayat, A. and Visser, A., New constructions of satisfaction classes, Unifying the Philosophy of Truth (Achourioti, T., Galinon, H., Fernández, J. M., and Fujimoto, K., editors), Springer-Verlag, Berlin, 2015, pp. 321–335.CrossRefGoogle Scholar
Feferman, S., Reflecting on incompleteness, this Journal, vol. 56 (1991), no. 1, pp. 1–49.Google Scholar
Fischer, M., Truth and speed-up. The Review of Symbolic Logic, vol. 7 (2014), no. 2, pp. 319–340.CrossRefGoogle Scholar
Friedman, H. and Sheard, M., An axiomatic approach to self-referential truth. Annals of Pure and Applied Logic, vol. 33 (1987), pp. 1–21.CrossRefGoogle Scholar
Hájek, P. and Pudlák, P., Metamathematics of First-Order Arithmetic, Springer-Verlag, Berlin, 1993.Google Scholar
Halbach, V., Axiomatic Theories of Truth, Cambridge University Press, Cambridge, 2011.CrossRefGoogle Scholar
Kaye, R., Models of Peano Arithmetic, Clarendon Press, Oxford, 1991.Google Scholar
Kossak, R. and Wcisło, B., Disjunctions with stopping condition. Bulletin of Symbolic Logic, accepted.Google Scholar
Kotlarski, H., Krajewski, S., and Lachlan, A., Construction of satisfaction classes for nonstandard models. Canadian Mathematical Bulletin, vol. 24 (1981), pp. 283–293.Google Scholar
Kripke, S., Outline of a theory of truth. The Journal of Philosophy, vol. 72 (1975), no. 19, pp. 690–716.CrossRefGoogle Scholar
Leigh, G., Conservativity for theories of compositional truth via cut elimination, this Journal, vol. 80 (2015), no. 3, pp. 845–865.Google Scholar
Pudlák, P., On the length of proofs of finitistic consistency statements in first order theories, Logic Colloquium 84 (Paris, J. B., Wilkie, A., and Wilmers, G., editors), 1986 .Google Scholar
Pudlák, P., The lengths of proofs, Handbook of Proof Theory (Buss, S. R., editor), Elsevier, Amsterdam, 1998, pp. 547–642.CrossRefGoogle Scholar
Simpson, S. G., Subsystems of Second Order Arithmetic, second ed., Perspectives in Logic, Cambridge University Press, Cambridge, 2009.CrossRefGoogle Scholar
McGee, Vann, How truthlike can a predicate be ? A negative result. Journal of Philosophical Logic, vol. 14 (1985), no. 4, pp. 399–410.CrossRefGoogle Scholar
Verbrugge, R., Feasible interpretations, Ph.D thesis, University of Amsterdam, 1993.Google Scholar
Wcisło, B. and Łełyk, M., Notes on bounded induction for the compositional truth predicate. The Review of Symbolic Logic, vol. 10 (2017), no. 3, pp. 455–480.CrossRefGoogle Scholar