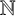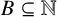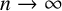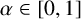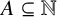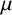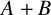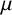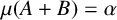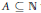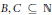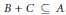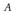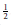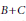Arithmetic quasidensities are a large family of real-valued set functions partially defined on the power set of $\mathbb {N}$, including the asymptotic density, the Banach density and the analytic density. Let $B \subseteq \mathbb {N}$ be a nonempty set covering $o(n!)$ residue classes modulo $n!$ as $n\to \infty $ (for example, the primes or the perfect powers). We show that, for each $\alpha \in [0,1]$, there is a set $A\subseteq \mathbb {N}$ such that, for every arithmetic quasidensity $\mu $, both A and the sumset $A+B$ are in the domain of $\mu $ and, in addition, $\mu (A + B) = \alpha $. The proof relies on the properties of a little known density first considered by Buck [‘The measure theoretic approach to density’, Amer. J. Math. 68 (1946), 560–580].

Erdős conjectured that for any set 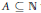$A\,\subseteq \,\mathbb{N}$ with positive lower asymptotic density, there are infinite sets 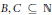$B,\,C\,\subseteq \,\mathbb{N}$ such that 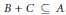$B\,+\,C\,\subseteq \,A$. We verify Erdős’ conjecture in the case where 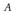$A$ has Banach density exceeding 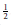$\frac{1}{2}$. As a consequence, we prove that, for 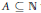$A\,\subseteq \,\mathbb{N}$ with positive Banach density (a much weaker assumption than positive lower density), we can find infinite 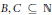$B,\,C\,\subseteq \,\mathbb{N}$ such that 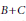$B\,+\,C$ is contained in the union of 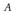$A$ and a translate of 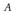$A$. Both of the aforementioned results are generalized to arbitrary countable amenable groups. We also provide a positive solution to Erdős’ conjecture for subsets of the natural numbers that are pseudorandom.

Erdős and Odlyzko proved that odd integers k such that k2n+1 is prime for some positive integer n have a positive lower density. In this paper, we characterize all arithmetic progressions in which natural numbers that can be expressed in the form (p−1)2−n (where p is a prime number) have a positive proportion. We also prove that an arithmetic progression consisting of odd numbers can be obtained from a covering system if and only if those integers in such a progression which can be expressed in the form (p−1)2−n have an asymptotic density of zero.