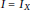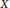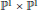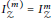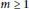1 results
The Minimal Free Resolution of Fat Almost Complete Intersections in ℙ1 × ℙ1
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 6 / 01 December 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1274-1291
- Print publication:
- 01 December 2017
-
- Article
-
- You have access
- Export citation
-
A current research theme is to compare symbolic powers of an ideal
$I$ with the regular powers of $I$. In this paper, we focus on the case where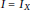 
$I\,=\,{{I}_{X}}$ is an ideal defining an almost complete intersection (ACI) set of points 
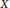$X$ in 
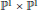${{\mathbb{P}}^{1}}\,\times \,{{\mathbb{P}}^{1}}$. In particular, we describe a minimal free bigraded resolution of a non-arithmetically Cohen-Macaulay (also non-homogeneous) set 
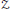$Z$ of fat points whose support is an ACI, generalizing an earlier result of Cooper et al. for homogeneous sets of triple points. We call 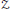$Z$ a fat ACI. We also show that its symbolic and ordinary powers are equal, i.e, 
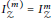$I_{Z}^{\left( m \right)}\,=\,I_{Z}^{m}$ for any 
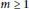$m\,\ge \,1$.
