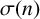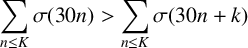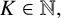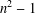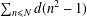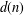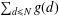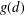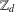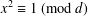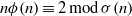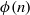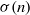4 results
ON A PROBLEM OF PONGSRIIAM ON THE SUM OF DIVISORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 13 September 2024, pp. 13-18
- Print publication:
- February 2025
-
- Article
-
- You have access
- HTML
- Export citation
ON THE NUMBER OF DIVISORS OF
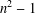 $n^{2}-1$
$n^{2}-1$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 02 October 2015, pp. 194-198
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
ON A VARIATION OF A CONGRUENCE OF SUBBARAO
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 04 February 2013, pp. 85-90
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
Asymptotics of poisson approximation to random discrete distributions: an analytic approach
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 448-491
- Print publication:
- June 1999
-
- Article
- Export citation