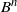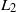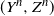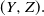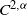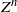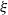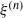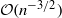3 results
Mean square rate of convergence for random walk approximation of forward-backward SDEs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. 735-771
- Print publication:
- September 2020
-
- Article
- Export citation
A EUROPEAN OPTION GENERAL FIRST-ORDER ERROR FORMULA
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 54 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 04 September 2013, pp. 248-272
-
- Article
-
- You have access
- Export citation
Approximation of control problems involving ordinary and impulsive controls
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 4 / 1999
- Published online by Cambridge University Press:
- 15 August 2002, pp. 159-176
- Print publication:
- 1999
-
- Article
- Export citation