Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-09T01:36:51.373Z Has data issue: false hasContentIssue false
  • English
  • Français

Mean square rate of convergence for random walk approximation of forward-backward SDEs

Part of: Stochastic processes Stochastic analysis

Published online by Cambridge University Press:  24 September 2020

Christel Geiss ,
Céline Labart  and
Antti Luoto
Christel Geiss*
Affiliation:
University of Jyvaskyla
Céline Labart*
Affiliation:
Univ. Grenoble Alpes, Univ. Savoie Mont Blanc, CNRS, LAMA
Antti Luoto*
Affiliation:
University of Jyvaskyla
*
*Postal address: Department of Mathematics and Statistics, University of Jyvaskyla, Finland, P.O. Box 35 (MaD) FI-40014.
**Postal address: Université Grenoble Alpes, Université Savoie Mont Blanc, CNRS, LAMA, 73000 Chambéry, France.
*Postal address: Department of Mathematics and Statistics, University of Jyvaskyla, Finland, P.O. Box 35 (MaD) FI-40014.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let (Y, Z) denote the solution to a forward-backward stochastic differential equation (FBSDE). If one constructs a random walk 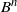$B^n$ from the underlying Brownian motion B by Skorokhod embedding, one can show 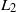$L_2$-convergence of the corresponding solutions 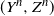$(Y^n,Z^n)$ to 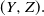$(Y, Z).$ We estimate the rate of convergence based on smoothness properties, especially for a terminal condition function in 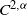$C^{2,\alpha}$. The proof relies on an approximative representation of 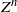$Z^n$ and uses the concept of discretized Malliavin calculus. Moreover, we use growth and smoothness properties of the partial differential equation associated to the FBSDE, as well as of the finite difference equations associated to the approximating stochastic equations. We derive these properties by probabilistic methods.

Keywords

Backward stochastic differential equationsapproximation schemefinite difference equationconvergence raterandom walk approximation

MSC classification

Primary: 60H10: Stochastic ordinary differential equations
Secondary: 60H35: Computational methods for stochastic equations 60G50: Sums of independent random variables; random walks 60H30: Applications of stochastic analysis (to PDE, etc.)
Type
Original Article
Information
Advances in Applied Probability , Volume 52 , Issue 3 , September 2020 , pp. 735 - 771
Check for updates
Copyright
© Applied Probability Trust 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alanko, S. (2015). Regression-based Monte Carlo methods for solving nonlinear PDEs. Doctoral Thesis, New York University.Google Scholar
Ankirchner, S., Kruse, T. and Urusov, M. (2019). Wasserstein convergence rates for coin tossing approximations of continuous Markov processes. Preprint. Available at https://arxiv.org/abs/1903.07880.Google Scholar
Bally, V. and Pagès, G. (2003). A quantization algorithm for solving multidimensional discrete-time optimal stopping problems. Bernoulli 9, 1003–1049.10.3150/bj/1072215199CrossRefGoogle Scholar
Bender, C. and Parczewski, P. (2018). Discretizing Malliavin calculus. Stoch. Proc. Appl. 128, 2489–2537.10.1016/j.spa.2017.09.014CrossRefGoogle Scholar
Bender, C. and Zhang, J. (2008). Time discretization and Markovian iteration for coupled FBSDEs. Ann. Appl. Prob. 18, 143–177.10.1214/07-AAP448CrossRefGoogle Scholar
Bouchard, B. and Touzi, N. (2004). Discrete-time approximation and Monte Carlo simulation of backward stochastic differential equations. Stoch. Proc. Appl. 111, 175–206.10.1016/j.spa.2004.01.001CrossRefGoogle Scholar
Briand, P., Delyon, B. and Mémin, J. (2001). Donsker-type theorem for BSDEs. Electron. Commun. Prob. 6, 1–14.10.1214/ECP.v6-1030CrossRefGoogle Scholar
Briand, P. and Labart, C. (2014). Simulation of BSDEs by Wiener chaos expansion. Ann. Appl. Prob. 24, 1129–1171.10.1214/13-AAP943CrossRefGoogle Scholar
Chassagneux, J.-F. (2014). Linear multistep schemes for BSDEs. SIAM J. Numer. Anal. 52, 2815–2836.10.1137/120902951CrossRefGoogle Scholar
Chassagneux, J.-F. and Crisan, D. (2014). Runge–Kutta schemes for backward stochastic differential equations. Ann. Appl. Prob. 24, 679–720.10.1214/13-AAP933CrossRefGoogle Scholar
Chassagneux, J.-F., Crisan, D. and Delarue, F. (2019). Numerical method for FBSDEs of McKean–Vlasov type. Ann. Appl. Prob. 29, 1640–1684.10.1214/18-AAP1429CrossRefGoogle Scholar
Chassagneux, J.-F. and Garcia Trillos, C. A. (2017). Cubature methods to solve BSDEs: error expansion and complexity control. Preprint. Available at https://arxiv.org/abs/1702.00999.Google Scholar
Chassagneux, J.-F. and Richou, A. (2015). Numerical stability analysis of the Euler scheme for BSDEs. SIAM J. Numer. Anal. 53, 1172–1193.10.1137/140977047CrossRefGoogle Scholar
Chassagneux, J.-F. and Richou, A. (2019). Rate of convergence for discrete-time approximation of reflected BSDEs arising in switching problems. Stoch. Proc. Appl. 129, 4597–4637.10.1016/j.spa.2018.12.009CrossRefGoogle Scholar
Chaudru de Raynal, P. E. and Garcia Trillos, C. A. (2015). A cubature based algorithm to solve decoupled McKean–Vlasov forward-backward stochastic differential equations. Stoch. Proc. Appl. 125, 2206–2255.10.1016/j.spa.2014.11.018CrossRefGoogle Scholar
Cheridito, P. and Stadje, M. (2013). BS $\Delta$Es and BSDEs with non-Lipschitz drivers: comparison, convergence and robustness. Bernoulli 19, 1047–1085.CrossRefGoogle Scholar
Crisan, D., Manolarakis, K. and Touzi, N. (2010). On the Monte Carlo simulation of BSDEs: an improvement on the Malliavin weights. Stoch. Proc. Appl. 120, 1133–1158.10.1016/j.spa.2010.03.015CrossRefGoogle Scholar
Delarue, F. and Menozzi, S. (2006). A forward-backward stochastic algorithm for quasi-linear PDEs. Ann. Appl. Prob. 16, 140–184.CrossRefGoogle Scholar
El Karoui, N., Peng, S. and Quenez, M. C. (1997). Backward stochastic differential equations in finance. Math. Finance 7, 1–71.CrossRefGoogle Scholar
Geiss, C., Geiss, S. and Gobet, E. (2012). Generalized fractional smoothness and $L_p$-variation of BSDEs with non-Lipschitz terminal conditions. Stoch. Proc. Appl. 122, 2078–2116.10.1016/j.spa.2012.02.006CrossRefGoogle Scholar
Geiss, C. and Labart, C. (2016). Simulation of BSDEs with jumps by Wiener chaos expansion. Stoch. Proc. Appl. 126, 2123–2162.CrossRefGoogle Scholar
Geiss, C., Labart, C. and Luoto, A. (2020). Random walk approximation of BSDEs with Hölder continuous terminal condition. Bernoulli 26, 159–190.10.3150/19-BEJ1120CrossRefGoogle Scholar
Gobet, E., Lemor, J.-P. and Warin, X. (2005). A regression-based Monte Carlo method to solve backward stochastic differential equations. Ann. Appl. Prob. 15, 2172–2202.CrossRefGoogle Scholar
Henry-Labordère, P., Tan, X. and Touzi, N. (2014). A numerical algorithm for a class of BSDEs via the branching process. Stoch. Proc. Appl. 124, 1112–1140.CrossRefGoogle Scholar
Jacod, J. and Shiryaev, A. N. (2003). Limit Theorems for Stochastic Processes. Springer, Berlin, Heidelberg.CrossRefGoogle Scholar
Jańczak-Borkowska, K. (2012). Discrete approximations of generalized RBSDE with random terminal time. Discuss. Math. Prob. Statist. 32, 69–85.CrossRefGoogle Scholar
Kruse, T and Popier, A. (2016). BSDEs with monotone generator driven by Brownian and Poisson noises in a general filtration. Stochastics 88, 491–539.CrossRefGoogle Scholar
Kruse, T. and Popier, A. (2017). $L_p$-solution for BSDEs with jumps in the case $p<2$. Stochastics 89, 1201–1227.CrossRefGoogle Scholar
Ma, J., Protter, P., San Martín, J. and Torres, S. (2007). Numerical method for backward stochastic differential equations. Ann. Appl. Prob. 12, 302–316.Google Scholar
Ma, J. and Zhang, J. (2002). Representation theorems for backward stochastic differential equations. Ann. Appl. Prob. 12, 1390–1418.Google Scholar
Martínez, M., San Martín, J. and Torres, S. (2011). Numerical method for reflected backward stochastic differential equations. Stoch. Anal. Appl. 29, 1008–1032.CrossRefGoogle Scholar
Mémin, J., Peng, S. and Xu, M. (2008). Convergence of solutions of discrete reflected backward SDE’s and simulations. Acta Math. Appl. Sin. Engl. Ser. 24, 1–18.CrossRefGoogle Scholar
Peng, S. and Xu, M. (2011). Numerical algorithms for backward stochastic differential equations with 1-d Brownian motion: convergence and simulations. Math. Modelling Numer. Anal. 45, 335–360.CrossRefGoogle Scholar
Privault, N. (2009). Stochastic Analysis in Discrete and Continuous Settings—With Normal Martingales. Springer, Berlin, Heidelberg.CrossRefGoogle Scholar
Tao, T. (2010). An Epsilon of Room, I: Real Analysis. American Mathematical Society, Providence, RI.Google Scholar
Toldo, S. (2006). Stability of solutions of BSDEs with random terminal time. ESAIM Prob. Statist. 10, 141–163.CrossRefGoogle Scholar
Toldo, S. (2007). Corrigendum to ‘Stability of solutions of BSDEs with random terminal time’. ESAIM Prob. Statist. 11, 381–384.CrossRefGoogle Scholar
Walsh, J. B. (2003). The rate of convergence of the binomial tree scheme. Finance Stoch. 7, 337–361.CrossRefGoogle Scholar
Weinan, E., Hutzenthaler, M., Jentzen, A. and Kruse, T. (2019). On multilevel Picard numerical approximations for high-dimensional nonlinear parabolic partial differential equations and high-dimensional nonlinear backward stochastic differential equations. J. Sci. Comput. 79, 1534–1571.Google Scholar
Yao, S. (2017). $L_p$ solutions of backward stochastic differential equations with jumps. Stoch. Proc. Appl. 127, 3465–3511.10.1016/j.spa.2017.03.005CrossRefGoogle Scholar
Zhang, J. (2001). Some fine properties of backward stochastic differential equations, with applications. Doctoral Thesis, Purdue University.Google Scholar
Zhang, J. (2004). A numerical scheme for BSDEs. Ann. Appl. Prob. 14, 459–488.CrossRefGoogle Scholar
Zhang, J. (2005). Representation of solutions to BSDEs associated with a degenerate FSDE. Ann. Appl. Prob. 15, 1798–1831.10.1214/105051605000000232CrossRefGoogle Scholar