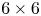The Floquet exponents of periodic field lines are studied through the variations of the magnetic action on the magnetic axis, which is assumed to be elliptical. The near-axis formalism developed by Mercier, Solov'ev and Shafranov is combined with a Lagrangian approach. The on-axis Floquet exponent is shown to coincide with the on-axis rotational transform. A discrete solution suitable for numerical implementation is introduced, which gives the Floquet exponents as solutions to an eigenvalue problem. This discrete formalism expresses the exponents as the eigenvalues of a $6\times 6$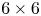 matrix.
matrix.