We obtain a complete topological classification of $k$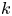 -folding map-germs on generic surfaces in $\mathbb {R}^3$
-folding map-germs on generic surfaces in $\mathbb {R}^3$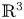 , discover new robust features of surfaces and recover, in a unified way, many of the robust features that were obtained previously by considering the contact of a surface with lines, planes or spheres.
, discover new robust features of surfaces and recover, in a unified way, many of the robust features that were obtained previously by considering the contact of a surface with lines, planes or spheres.