1 results
Semistationary and stationary reflection
-
- Journal:
- The Journal of Symbolic Logic / Volume 73 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 12 March 2014, pp. 181-192
- Print publication:
- March 2008
-
- Article
- Export citation

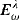 ≔ {
≔ {