Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
DOEBLER, PHILIPP
2013.
RADO'S CONJECTURE IMPLIES THAT ALL STATIONARY SET PRESERVING FORCINGS ARE SEMIPROPER.
Journal of Mathematical Logic,
Vol. 13,
Issue. 01,
p.
1350001.
Sakai, Hiroshi
and
Veličković, Boban
2015.
Stationary reflection principles and two cardinal tree properties.
Journal of the Institute of Mathematics of Jussieu,
Vol. 14,
Issue. 1,
p.
69.
USUBA, Toshimichi
2016.
Reflection principles for $\omega_2$ and the semi-stationary reflection principle.
Journal of the Mathematical Society of Japan,
Vol. 68,
Issue. 3,
Zhang, Jing
2020.
Rado’s Conjecture and its Baire version.
Journal of Mathematical Logic,
Vol. 20,
Issue. 01,
p.
1950015.
Fuchino, Sakaé
Rodrigues, André Ottenbreit Maschio
and
Sakai, Hiroshi
2021.
Strong downward Löwenheim–Skolem theorems for stationary logics, I.
Archive for Mathematical Logic,
Vol. 60,
Issue. 1-2,
p.
17.


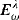 ≔ {
≔ {