1 results
Quantum Deformations of Simple Lie Algebras
-
- Journal:
- Canadian Mathematical Bulletin / Volume 40 / Issue 2 / 01 June 1997
- Published online by Cambridge University Press:
- 20 November 2018, pp. 143-148
- Print publication:
- 01 June 1997
-
- Article
-
- You have access
- Export citation
-
It is shown that every simple complex Lie algebra 𝔤 admits a 1-parameter family 𝔤q of deformations outside the category of Lie algebras. These deformations are derived from a tensor product decomposition for Uq(𝔤)-modules; here Uq(𝔤) is the quantized enveloping algebra of 𝔤. From this it follows that the multiplication on 𝔤q is Uq(𝔤)-invariant. In the special case 𝔤 =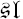
(2), the structure constants for the deformation 𝔤 (2)q are obtained from the quantum Clebsch-Gordan formula applied to V(2)q ⊗ V(2)q; here V(2)q is the simple 3-dimensional Uq(𝔤(2))-module of highest weight q2.
(2), the structure constants for the deformation 𝔤 (2)