We study the relative 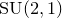 $\mathrm {SU}(2,1)$-character varieties of the one-holed torus, and the action of the mapping class group on them. We use an explicit description of the character variety of the free group of rank two in
$\mathrm {SU}(2,1)$-character varieties of the one-holed torus, and the action of the mapping class group on them. We use an explicit description of the character variety of the free group of rank two in 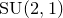 $\mathrm {SU}(2,1)$ in terms of traces, which allow us to describe the topology of the character variety. We then combine this description with a generalization of the Farey graph adapted to this new combinatorial setting, using ideas introduced by Bowditch. Using these tools, we can describe an open domain of discontinuity for the action of the mapping class group which strictly contains the set of convex cocompact characters, and we give several characterizations of representations in this domain.
$\mathrm {SU}(2,1)$ in terms of traces, which allow us to describe the topology of the character variety. We then combine this description with a generalization of the Farey graph adapted to this new combinatorial setting, using ideas introduced by Bowditch. Using these tools, we can describe an open domain of discontinuity for the action of the mapping class group which strictly contains the set of convex cocompact characters, and we give several characterizations of representations in this domain.
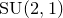 $\mathrm {SU}(2,1)$-character variety of the one-holed torus
$\mathrm {SU}(2,1)$-character variety of the one-holed torus